当前位置:网站首页>Classical graph theory, depth first and breadth first, topology, prim and krukal, it's time to review
Classical graph theory, depth first and breadth first, topology, prim and krukal, it's time to review
2022-06-11 08:26:00 【Van Gogh's pig V】
List of articles
chart
Graph is widely used in life , The depth first and breadth first algorithms you usually hear are based on graphs .
The concept of graph is very simple , There is no retelling here , Wait until Xiaobian talks about the example , It suddenly opened up .
analysis
How do we store a graph in our code ? In fact, there are two common ways
One is to use the collar matrix , It's a two-dimensional array , Array subscript is the representation of graph point ,a[i][j]=1 It means i Point and j Point connectivity , If it is 0 Indicates disconnected .
The other is adjacency table , That is, a one-dimensional array is used to represent these graph points , Then each location is linked to a queue or linked list , The chain stores the points directly connected to the point .( Is directly connected , Not indirectly connected , such as a-b-c,a and b Is directly connected )
Code
package com.hyb.ds. chart ;
import sun.misc.Queue;
public class Graph {
// spot
private final int v;
// edge
private int e;
private final Queue<Integer>[] queues;
public Graph(int v){
this.v=v;
this.e=0;
queues= new Queue[v];
for (int i = 0; i < v; i++) {
queues[i]= new Queue<Integer>();
}
}
public int getV(){
return v;
}
public int getE(){
return e;
}
public void addE(int w,int m){
queues[w].enqueue(m);
queues[m].enqueue(w);
e++;
}
public Queue<Integer> getE(int i){
return queues[i];
}
}
class Test{
public static void main(String[] args) {
Graph graph = new Graph(13);
graph.addE(0,1);
graph.addE(0,2);
graph.addE(0,6);
graph.addE(0,5);
graph.addE(5,3);
graph.addE(5,4);
graph.addE(3,4);
graph.addE(4,6);
graph.addE(7,8);
graph.addE(9,10);
graph.addE(9,11);
graph.addE(9,12);
graph.addE(11,12);
DFS dfs = new DFS(graph, 0);
System.out.println(dfs.getCount());
System.out.println(dfs.marked(7));
System.out.println(dfs.marked(6));
System.out.println(dfs.marked(3));
}
}
Depth-first search

Look at the undirected graph above , Depth first search is mainly to judge and 0 A point that connects points , from 0 Start off , The first 6 go , The road passed is marked as passed , as long as 6 I haven't been walked by myself , Just go to 6, then 6 Continue to drill down with this rule , If you find that all the points connected by the surrounding bytes have passed , Go back the same way , That is, if you search 5 This point , Find out 0,3,4 All searched , Just return to the original point , such as 3, Came to 3 I found that I searched around , Just go back to 4, Keep returning and constantly explore whether there are any points around that have not been searched , Search if it exists . There are no searchable points until the beginning , ends .
package com.hyb.ds. chart ;
import com.hyb.ds. queue .ArrayQueue;
import sun.misc.Queue;
import java.util.Enumeration;
public class DFS {
private boolean[] marked;
// Initializes the number of connections to vertices
private int count;
public DFS(Graph graph,int first){
this.marked=new boolean[graph.getV()];
this.count=0;
dfs(graph,first);
}
public void dfs(Graph graph,int first){
marked[first]=true;
Queue<Integer> e = graph.getE(first);
Enumeration<Integer> elements = e.elements();
while (elements.hasMoreElements()){
Integer integer = elements.nextElement();
if (!marked(integer)){
dfs(graph,integer);
}
}
count++;
}
// Determine whether a point is connected to a vertex
public boolean marked(int w){
return marked[w];
}
public int getCount(){
return count;
}
}
As you can see from the code above , When we use adjacency tables to store graphs , The depth first search path is , First search in the queue from the corresponding point , If you find a point that has not been searched , The queue that turns to this point starts searching , Instead of searching in the original queue .
In this picture , If you need to find a path , That is, output the paths of all the arriving nodes , Just recreate an array .
Breadth first search
Breadth first search is the opposite of depth first search , Depth first , Look deep , That is, the point can be connected , Go to the child node of the point . Go deep into the child nodes of the child nodes to find , Until it is found that all nodes near a child node have been searched , Continue the rule of turning back on the same route .
And breadth first search , Is to find all nearby nodes that can be connected , Then go to a connected node to find its child nodes that can be connected nearby .
That is, we can see from the picture above , If breadth first search is used :
0->5->1->2->6 5->3->4
Code implementation ideas :
We can use a secondary queue to implement , Join the current point , Then when the queue is not empty , Just pop up the queue element , The first pop-up is the current point , So find the extended adjacency table according to the current point , Keep searching , Keep joining the team , After that, when the queue is cycled, you can click the search point , According to the principle of first in, first out , To find the corresponding adjacency table search .
This is different from depth first , You can imagine , Depth first is to find a point in the adjacency table , Immediately recurse the adjacency table of the point and continue to search . And this breadth first is to first search all the points in the adjacency table of a point to join the team , Then search the adjacency table of each point according to the principle of first in first out .
import sun.misc.Queue;
import java.util.Enumeration;
public class BFS {
private boolean[] marked;
private int count;
// Secondary queue
private Queue<Integer> queues;
public BFS(Graph graph,int first) throws InterruptedException {
marked=new boolean[graph.getV()];
this.count=0;
queues=new Queue<Integer>();
bfs(graph,first);
}
public void bfs(Graph graph,int first) throws InterruptedException {
marked[first]=true;
queues.enqueue(first);
while (!queues.isEmpty()){
Integer dequeue = queues.dequeue();
Queue<Integer> e = graph.getE(dequeue);
Enumeration<Integer> elements = e.elements();
while (elements.hasMoreElements()){
Integer element = elements.nextElement();
if (!marked[element]){
queues.enqueue(element);
marked[element]=true;
}
}
System.out.println(" Search point ->"+dequeue);
count++;
}
}
// Determine whether a point is connected to a vertex
public boolean marked(int w){
return marked[w];
}
public int getCount(){
return count;
}
}
class Test1{
public static void main(String[] args) throws InterruptedException {
Graph graph = new Graph(13);
graph.addE(0,1);
graph.addE(0,2);
graph.addE(0,6);
graph.addE(0,5);
graph.addE(5,3);
graph.addE(5,4);
graph.addE(3,4);
graph.addE(4,6);
graph.addE(7,8);
graph.addE(9,10);
graph.addE(9,11);
graph.addE(9,12);
graph.addE(11,12);
BFS dfs = new BFS(graph, 0);
System.out.println(dfs.getCount());
System.out.println(dfs.marked(7));
System.out.println(dfs.marked(6));
System.out.println(dfs.marked(3));
}
}
Unimpeded works
Same as the previous topic , However, the demand at this time is to judge whether the two cities are connected
Graph graph = new Graph(20);
graph.addE(0,1);
graph.addE(6,9);
graph.addE(3,8);
graph.addE(5,11);
graph.addE(2,12);
graph.addE(6,10);
graph.addE(4,8);
BFS dfs = new BFS(graph, 9);
System.out.println(dfs.getCount());
System.out.println(dfs.marked(8));
System.out.println(dfs.marked(10));
Directed graph
The above explanations are all undirected graphs , That is, any two points can be connected no matter from which point they are triggered , A directed graph can only connect from the beginning to the end .
We can use the above code to make a simple modification , Add a Boolean field , If there is an incoming Boolean value of true, Then it means to create a directed graph , When inserting an edge , Just connect one edge .


At the same time, we can add an interesting function : Get the inverted graph of the graph :
private Graph reverseGraph(){
Graph graph = new Graph(v);
for (int i = 0; i < v; i++) {
Queue<Integer> e = getE(i);
Enumeration<Integer> elements = e.elements();
while (elements.hasMoreElements()){
Integer integer = elements.nextElement();
addE(integer,i);
}
}
return graph;
}
A topological sort
For a directed graph , set up G=(V,E),V Represents a vertex set ,E It represents the edge relationship between vertices , if Vi -> Vj The path of existence , be Vi Must be in line with Vj Before , Then we call such a vertex sequence a topological sequence , The process of forming a topological sequence is called topological sorting .
As you can see from the above definition , There are two prerequisites for topological sorting : One is directed graph , Second, it is not allowed to arc the circular graph
Pictured above , After sorting, it is shown in the following figure 
The topological sequence consists of 1->3->4->5 0->3->4->5 0->2->4->5
Check loop
No matter which way you use Topology , First, check whether there is a loop , The topology must be carried out without loops
- We can use the depth first algorithm , Let all nodes go through directly .
- Here we need to design two marker bits , One is the marker bit of the large loop , What is a big cycle ? That is, depth first search starting from all nodes , And there is also a small cycle mark bit , The small cycle mark bit records the road from the start point to the end point . This small loop is to be recalled during backtracking .
import sun.misc.Queue;
import java.util.Enumeration;
public class DirectedCycle {
// Mark whether the road has been crossed ( Great circulation )
private boolean[] marked;
// Mark whether there is a loop
private boolean hasCycle;
// Auxiliary array , The subscript corresponds to the node , Value corresponds to whether it has been accessed ( Small cycle of monitoring ring )
private boolean[] directed;
public DirectedCycle(Graph graph){
int v = graph.getV();
this.marked=new boolean[v];
this.directed=new boolean[v];
for (int i = 0; i < v; i++) {
if (!marked[i]){
dfs(graph,i);
}
}
}
private void dfs(Graph graph,int first){
marked[first]=true;
directed[first]=true;
Queue<Integer> e = graph.getE(first);
Enumeration<Integer> elements = e.elements();
while (elements.hasMoreElements()){
Integer integer = elements.nextElement();
if (!marked[integer]){
dfs(graph,integer);
}
// If you find in a small loop , This point has been visited , It means there is a ring
if (directed[integer]){
hasCycle=true;
return;
}
}
directed[first]=false;
}
public boolean isHasCycle(){
return hasCycle;
}
}
Click on the stack
If the diagram does not have a loop , Description of topologies , Is to find reachable sequences , So the core implementation here is to click on the stack .
It is also a depth first search method , Search to the deepest point , Then, when backtracking, let the point be put on the stack , In this way, a connected link is obtained
package com.hyb.ds. chart ;
import com.hyb.ds. Binary tree .PageTree;
import com.hyb.ds. Design patterns . The proxy pattern . A dynamic proxy .TargetObj;
import sun.misc.Queue;
import java.util.Enumeration;
import java.util.List;
import java.util.Stack;
public class TopSort {
// Have you ever been interviewed
private boolean[] marked;
// After recursion, the node is stored in the stack in reverse
private Stack<Integer> stack;
public TopSort(Graph graph){
int v = graph.getV();
marked=new boolean[v];
stack=new Stack<>();
// Because it's a directed graph , All to cycle through all vertices
for (int i = 0; i < 2; i++) {
if (!marked[i]){
dfs(graph,i);
}
}
}
private void dfs(Graph graph,int first){
marked[first]=true;
// After depth first, put the vertex on the stack
System.out.println(" Stack point ->"+first);
Queue<Integer> e = graph.getE(first);
Enumeration<Integer> elements = e.elements();
while (elements.hasMoreElements()){
flag=false;
Integer integer = elements.nextElement();
if (!marked[integer]){
dfs(graph,integer);
stack.push(first);
}
public Stack<Integer> getStack(){
return stack;
}
public List<Stack<Integer>> list(){
return list;
}
}
Implement Topology
The implementation topology is the sum of the above two steps
package com.hyb.ds. chart ;
import java.util.Stack;
public class TopoSort {
private Stack<Integer> stack;
public TopoSort(Graph graph){
DirectedCycle directedCycle = new DirectedCycle(graph);
boolean hasCycle = directedCycle.isHasCycle();
if (!hasCycle){
TopSort topSort = new TopSort(graph);
stack=topSort.getStack();
}
}
public boolean isCycle(){
return stack==null;
}
public Stack<Integer> getStack(){
return stack;
}
}
class Test4{
public static void main(String[] args) {
Graph graph = new Graph(6, true);
graph.addE(0,2);
graph.addE(0,3);
graph.addE(1,3);
graph.addE(2,4);
graph.addE(3,4);
graph.addE(4,5);
TopoSort topoSort = new TopoSort(graph);
Stack<Integer> stack = topoSort.getStack();
for (Integer i :
stack) {
System.out.println(i);
}
}
}
And what you get is 543201, But as a result, Xiaobian feels that it is not very friendly , Because this sequence can only show the interconnection between some points here , In fact, it is impossible to get a connected sequence from it without the help of external forces , For example, here 0 and 1 In fact, it is disconnected , Everyone is the starting point , Can be connected to 3 nothing more .
Upgrade topology
It can output to all sequences that can be connected in one direction , These sequences we use a list Combine to store .
The key to getting these sequences is , It is also a depth first search for all points , But each node actually participates in depth first search , That is, the stack storing nodes should be out of the stack during backtracking ,mark The flag bit also returns to its original state , Let the new depth first search not be affected by the previous one .
We are looking at the previous topological sequence , Will record all the points passed , Finally, it returns to a stack , This is actually somewhat ambiguous , Because we don't know which two points are connected , Adding these two points is the degree of 0 What about the starting point of ? So you really want to get all the connected sequences , Only means can be used to make all points depth first , Then record the distance of each depth first node .
Of course , This is also established without circular connections .
package com.hyb.ds. chart ;
import com.hyb.ds. Binary tree .PageTree;
import com.hyb.ds. Design patterns . The proxy pattern . A dynamic proxy .TargetObj;
import sun.misc.Queue;
import java.util.ArrayList;
import java.util.Enumeration;
import java.util.List;
import java.util.Stack;
public class TopSort {
// Have you ever been interviewed
private boolean[] marked;
// After recursion, the node is stored in the stack in reverse
private Stack<Integer> stack;
// Store reachable paths
private List<Stack<Integer>> list;
// place list Added by
private boolean flag;
public TopSort(Graph graph){
int v = graph.getV();
marked=new boolean[v];
stack=new Stack<>();
list=new ArrayList<>();
// Because it's a directed graph , All to cycle through all vertices
for (int i = 0; i < v; i++) {
if (!marked[i]){
dfs(graph,i);
}
}
}
private void dfs(Graph graph,int first){
flag=false;
marked[first]=true;
// After depth first, put the vertex on the stack
stack.push(first);
System.out.println(" Stack point ->"+first);
Queue<Integer> e = graph.getE(first);
Enumeration<Integer> elements = e.elements();
while (elements.hasMoreElements()){
Integer integer = elements.nextElement();
if (!marked[integer]){
dfs(graph,integer);
}
}
if (!flag && !stack.empty()){
Stack<Integer> s = new Stack<>();
for (Integer i :
stack) {
s.push(i);
}
list.add(s);
flag=true;
}
stack.pop();
marked[first]=false;
}
public Stack<Integer> getStack(){
return stack;
}
public List<Stack<Integer>> list(){
return list;
}
}
After upgrading the topology , You can Topo The function also has list It can be tested after the combination .
Minimum spanning tree
In a weighted graph , Find some paths , These paths require that all connectivity points be connected , To achieve path and minimum .
Prim Algorithm
This algorithm is a classical algorithm for finding the minimum spanning tree , As shown in the figure above , The steps of the algorithm are : If from 0 Start , Find the point set directly adjacent to it , Such as 4,7,2,6, Then find a point with the shortest path in these point sets , Such as 7, And then let 7 Included in the 0 Camps , take 7 and 0 As a whole , For example, as a point , Again, find the set of points directly connected around , For example, in addition to the original point set , also 5,1, These two points are different from the original 4,7,2,6 Form a set of points .
There are two points to note in the set of construction points :
- The first is from 4,7,2,6 In this set of points, we find the relation between 0 Connect to the nearest point 7 after , To put 7 Delete from the point set , because 7 Included in the 0 After your camp , It has been regarded as a point , You don't need to see 7 and 0 Between .
- The second is when 7 Included in the 0 after , Look at the directly connected points around , Exist 4 Of , But this 4 Already with 0 Connected , That is to say, before you start 0 In search of ,4 It has been included in the point set , When you from 7-0 When I started watching , You can't just 4 The inclusion points are set , But to judge 7 To 4 The path and 4 To 0 Which path is smaller , If the former is smaller , Just overwrite the original value , If the former is larger , There is no need to cover .
Code thinking :
- Since we are going to traverse every connected point , So it requires a cycle , This can be a queue , Because the queue is more convenient , We will first 0 The team , And then out of the team , Use this point of the first out team to find the point set , After finding , Let's talk about the points on the shortest path , This included operation is to add 7 Put it in the queue , In this way, the included points have a sequence to find the surrounding point set
- The point set is stored in , Have an array , The storage of this array is very particular , The subscript is the corresponding point of the current point , The value is the distance between the two points , such as 0 and 7 These two points , If you put it in the set of points, it will be subscript 7, The value is 7 and 0 Length between .
- After a collection of points , Enter a function to compare and find the smallest point in the array .
Code steps
- First, we construct an object , An object is an edge object between points
public class EdgeW implements Comparable {
private int w;
private int v;
private double weight;
public EdgeW(int w, int v, double weight){
this.w=w;
this.v=v;
this.weight=weight;
}
public double getWeight() {
return weight;
}
public int getW() {
return w;
}
public int getV() {
return v;
}
@Override
public int compareTo(Object o) {
if (o instanceof EdgeW){
EdgeW e=(EdgeW) o;
return Double.compare(this.getWeight(), e.getWeight());
}
return -2;
}
@Override
public boolean equals(Object obj) {
if (obj instanceof EdgeW){
EdgeW e=(EdgeW) obj;
return this.v == e.v && this.w == e.w && this.weight == e.weight;
}
return false;
}
@Override
public String toString() {
return "["+this.w+"<->"+this.v+" weight:"+weight+"]";
}
public int other(int i) {
if (i==v)
return w;
else
return v;
}
}
- Then construct a weight graph :
package com.hyb.ds. chart ;
import sun.misc.Queue;
import java.util.Enumeration;
public class WeightGraph {
// The vertices
private int v;
// edge
private int e;
private Queue<EdgeW>[] edgeQueues;
private boolean type;
public WeightGraph(int v,boolean type) {
this.v = v;
this.edgeQueues = new Queue[v];
this.type = type;
for (int i = 0; i < v; i++) {
edgeQueues[i]=new Queue<EdgeW>();
}
}
public int getV(){
return v;
}
public int getW(){
return e;
}
public void addEdge(EdgeW edge){
int w = edge.getW();
int v = edge.getV();
edgeQueues[w].enqueue(edge);
if (!type){
edgeQueues[v].enqueue(edge);
}
e++;
}
// Get and vertex v All associated edges
public Queue<EdgeW> getEdges(int v){
return edgeQueues[v];
}
// Get all sides
public Set<EdgeW> edges(){
HashSet<EdgeW> edgeWS = new HashSet<>();
for (int i = 0; i < this.v; i++) {
Queue<EdgeW> edges = getEdges(i);
Enumeration<EdgeW> elements =
edges.elements();
while (elements.hasMoreElements()){
EdgeW edgeW = elements.nextElement();
edgeWS.add(edgeW);
}
}
return edgeWS;
}
}
- Here is the core code :
package com.hyb.ds. chart ;
import sun.misc.Queue;
import java.util.ArrayList;
import java.util.Enumeration;
import java.util.List;
public class PrimMST {
// Save the existing shortest path
private List<EdgeW> edgeTo;
// The index represents the vertex , Determine whether the vertex is already in the tree
private boolean[] marked;
// Store the effective crosscutting edges of the shard , The index is the closest point to that point ( Not the current point ), The value is the edge object
private EdgeW[] pq;
public PrimMST(WeightGraph graph) throws InterruptedException {
int v = graph.getV();
edgeTo =new ArrayList<>();
marked=new boolean[v];
pq =new EdgeW[v];
visit(graph,0);
}
public void visit(WeightGraph graph,int v) throws InterruptedException {
// Create a queue of split points
Queue<Integer> queue=new Queue<>();
// Let the first point come in for the first time
queue.enqueue(v);
// When the queue is not empty
while (!queue.isEmpty()){
// Spit out the first entry point in the queue
Integer dequeue = queue.dequeue();
// Mark that the point has been visited
marked[dequeue]=true;
// Get the queue of all directly connected points of the point
Queue<EdgeW> edges = graph.getEdges(dequeue);
// Traverse the queue , Find the point with its minimum path
Enumeration<EdgeW> elements = edges.elements();
while (elements.hasMoreElements()){
// Find an edge
EdgeW edgeW = elements.nextElement();
// Get the corresponding point of the current point on this edge
int other = edgeW.other(dequeue);
// If this has been regarded as dequue O 'clock , Just skip it
if (marked[other])
continue;
// If the edge that this point extends is already pq Array
if (pq[other]==null){
// If other The extended edge is not in the array , Just join in
pq[other]=edgeW;
}else {
// Compare the current other Whether the edge of the point is smaller than the original one
if (edgeW.getWeight() < pq[other].getWeight()) {
// If the weight of the current edge is smaller than that of the existing edge , Instead of it
pq[other] = edgeW;
}
}
}
// According to what you get pq Find the smallest edge in the array
int j = findMinW(pq);
// Back to the original point, there is no need to join the team again
if (j!=0){
queue.enqueue(j);
}
}
}
private int findMinW(EdgeW[] pq) {
EdgeW x=new EdgeW(0,0,Double.MAX_VALUE);
int j=0;
for (int i = 1; i < pq.length; i++) {
if (pq[i]!=null){
if (pq[i].getWeight()<x.getWeight()){
x=pq[i];
j=i;
}
}
}
// Prevent returning to the original point will list Things in the collection
// Instead of
if (j!=0){
int first = x.other(j);
edgeTo.add(new EdgeW(first,j,x.getWeight()));
// Remove the smallest edge from the array record
pq[j]=null;
}
return j;
}
public List<EdgeW> getEdges(){
return edgeTo;
}
}
class Test5{
public static void main(String[] args) throws InterruptedException {
WeightGraph weightGraph = new WeightGraph(8, false);
EdgeW edgeW = new EdgeW(0, 2, 0.26);
EdgeW edgeW1 = new EdgeW(0, 7, 0.16);
EdgeW edgeW2 = new EdgeW(0, 4, 0.38);
EdgeW edgeW3 = new EdgeW(0, 6, 0.58);
EdgeW edgeW4 = new EdgeW(6, 2, 0.40);
EdgeW edgeW7 = new EdgeW(6, 3, 0.52);
EdgeW edgeW8 = new EdgeW(6, 4, 0.93);
EdgeW edgeW5 = new EdgeW(2, 7, 0.34);
EdgeW edgeW6 = new EdgeW(2, 3, 0.17);
EdgeW edgeW9 = new EdgeW(2, 1, 0.36);
EdgeW edgeW11 = new EdgeW(7, 4, 0.37);
EdgeW edgeW12 = new EdgeW(7, 5, 0.28);
EdgeW edgeW13 = new EdgeW(7, 1, 0.19);
EdgeW edgeW18 = new EdgeW(7, 2, 0.34);
EdgeW edgeW14 = new EdgeW(5, 1, 0.32);
EdgeW edgeW15 = new EdgeW(5, 4, 0.35);
EdgeW edgeW16 = new EdgeW(1, 3, 0.29);
weightGraph.addEdge(edgeW);
weightGraph.addEdge(edgeW7);
weightGraph.addEdge(edgeW8);
weightGraph.addEdge(edgeW9);
weightGraph.addEdge(edgeW11);
weightGraph.addEdge(edgeW12);
weightGraph.addEdge(edgeW13);
weightGraph.addEdge(edgeW18);
weightGraph.addEdge(edgeW14);
weightGraph.addEdge(edgeW15);
weightGraph.addEdge(edgeW16);
weightGraph.addEdge(edgeW1);
weightGraph.addEdge(edgeW2);
weightGraph.addEdge(edgeW3);
weightGraph.addEdge(edgeW4);
weightGraph.addEdge(edgeW5);
weightGraph.addEdge(edgeW6);
PrimMST primMST = new PrimMST(weightGraph);
List<EdgeW> edges = primMST.getEdges();
for (EdgeW e :
edges) {
System.out.println(e.toString());
}
}
}
explain : The steps of recording data structure and algorithm in the small series refer to the dark horse monk Silicon Valley . This minimum spanning tree is a reference to the former , Originally, I watched the video and did it , But I found that the video of dark horse has many disadvantages , The minimum spanning tree here is an example , Complicated the simple problem , As for how complicated , You can see the dark horse .
Kruskal Algorithm
This algorithm is simpler than the previous one , This algorithm looks at the whole situation , That is, to traverse the set of edges of the graph , Then find the smallest side , Until these edges are connected to form a minimum spanning tree .
As shown in the figure above : Let's go through all the edges first , Find the smallest edge , If so 3-2, So let this side be included in Set Collection . Traverse the remaining edges again , If this time 7-0, will 7-0 Included in the Set Collection .
The difficulty here is , If we get two sides 3-2 and 2-6 After the collection is included , When traversing, if you find 3-6 What about the smallest of the remaining edges ? This is certainly the case , But we cannot include it in Set in , Because this is not the minimum spanning tree .
In fact, this problem can be solved skillfully by using and searching sets , For example, we are getting 3-2 and 2-6 After these two edges are combined into the set , You can also put these two sides into the search set , Also explains 3-2-6 It's connected , At this time, if you find 3-6 Is the smallest of the remaining edges , We can first judge whether the two points are connected , If it is disconnected , Can be incorporated into Set in , If it's connected , Then it can not be incorporated into the minimum spanning tree
package com.hyb.ds. chart ;
import com.hyb.ds. Union checking set .UF;
import java.util.*;
public class Kruskal {
private Set<EdgeW> set;
private UF uf;
public Kruskal(WeightGraph graph){
set=new HashSet<>();
Set<EdgeW> edges = graph.edges();
int size = edges.size();
int v = graph.getV();
uf=new UF(v);
for (int i = 0; i < size; i++) {
kruskal(edges);
}
}
private void kruskal(Set<EdgeW> edges) {
Iterator<EdgeW> iterator = edges.iterator();
EdgeW edgeW=new EdgeW(-1,-1,Double.MAX_VALUE);
while (iterator.hasNext()){
EdgeW w = iterator.next();
if (w.getWeight()<edgeW.getWeight()){
edgeW=w;
}
}
int w = edgeW.getW();
int v = edgeW.other(w);
if (!uf.connected(w,v)){
uf.unioned(w,v);
set.add(edgeW);
}
edges.remove(edgeW);
}
public Set<EdgeW> getSet(){
return set;
}
}
class Test6{
public static void main(String[] args) throws InterruptedException {
WeightGraph weightGraph = new WeightGraph(8, false);
EdgeW edgeW = new EdgeW(0, 2, 0.26);
EdgeW edgeW1 = new EdgeW(0, 7, 0.16);
EdgeW edgeW2 = new EdgeW(0, 4, 0.38);
EdgeW edgeW3 = new EdgeW(0, 6, 0.58);
EdgeW edgeW4 = new EdgeW(6, 2, 0.40);
EdgeW edgeW7 = new EdgeW(6, 3, 0.52);
EdgeW edgeW8 = new EdgeW(6, 4, 0.93);
EdgeW edgeW5 = new EdgeW(2, 7, 0.34);
EdgeW edgeW6 = new EdgeW(2, 3, 0.17);
EdgeW edgeW9 = new EdgeW(2, 1, 0.36);
EdgeW edgeW11 = new EdgeW(7, 4, 0.37);
EdgeW edgeW12 = new EdgeW(7, 5, 0.28);
EdgeW edgeW13 = new EdgeW(7, 1, 0.19);
EdgeW edgeW18 = new EdgeW(7, 2, 0.34);
EdgeW edgeW14 = new EdgeW(5, 1, 0.32);
EdgeW edgeW15 = new EdgeW(5, 4, 0.35);
EdgeW edgeW16 = new EdgeW(1, 3, 0.29);
weightGraph.addEdge(edgeW);
weightGraph.addEdge(edgeW7);
weightGraph.addEdge(edgeW8);
weightGraph.addEdge(edgeW9);
weightGraph.addEdge(edgeW11);
weightGraph.addEdge(edgeW12);
weightGraph.addEdge(edgeW13);
weightGraph.addEdge(edgeW18);
weightGraph.addEdge(edgeW14);
weightGraph.addEdge(edgeW15);
weightGraph.addEdge(edgeW16);
weightGraph.addEdge(edgeW1);
weightGraph.addEdge(edgeW2);
weightGraph.addEdge(edgeW3);
weightGraph.addEdge(edgeW4);
weightGraph.addEdge(edgeW5);
weightGraph.addEdge(edgeW6);
Kruskal kruskal = new Kruskal(weightGraph);
Set<EdgeW> set = kruskal.getSet();
for (EdgeW next : set) {
System.out.println(next.toString());
}
}
}
边栏推荐
- Introduction to the principles of linkedblockingqueue, arrayblockingqueue, synchronousqueue, concurrentlinkedqueue and transferqueue
- Summary of embedded software interview questions
- Asynchronous notification mechanism of character device driver
- BFS on tree (tree breathing first search)
- What does it mean to buy a single-mode, dual-mode and Rechargeable Wireless Mouse
- Design of optimization table
- Pg/oracle database ASCII code to string custom function
- 盘它!用「飞项」轻松管理各类型项目
- Basic use of typescripy class
- Training yolov4 CSP model using coco dataset
猜你喜欢

torch. nn. functional. pad

盘它!用「飞项」轻松管理各类型项目
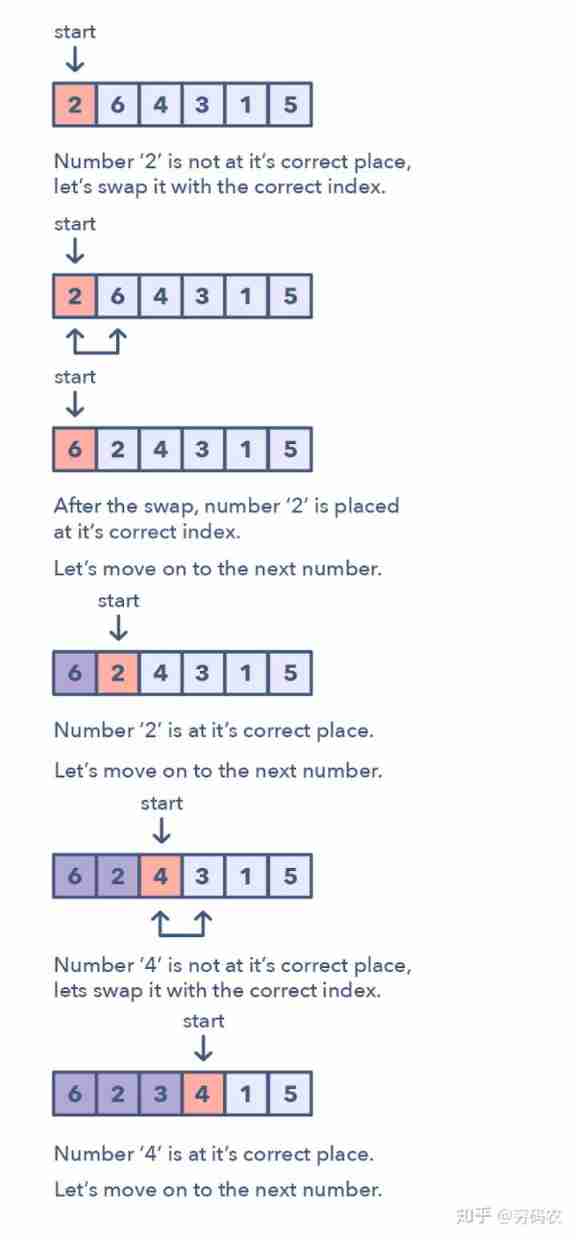
Cyclic sort

进程控制:进程等待(回收子进程)

Uniapp plug-in development

(transformation) tree, binary tree and forest transformation principle

Study the Analects of entanglement

Solve notimplementederror: layer XX has arguments in`__ init__` and therefore must override `get_ config`

torch. roll

Web design and website planning assignment 14 add background music to the video
随机推荐
Typescript enumeration
【CVPR2022】QueryDet论文精读
CentOS essay 03:centos8.2 installing MySQL
Web design and website planning assignment 14 add background music to the video
Empty difference between postgrepsql and Oracle
qiao-npms:获取npm包下载量
Js学习基础document.write在页面中写一行文字
These gadgets are also very easy to use
Process control: process waiting (recycling child processes)
结果和目标出入太大?不妨借助目标管理精准直达目标!
[software tools] screen recording software captura
Post - form data of interface test
Typescript type alias
torch. nn. functional. pad
Typescript unknown type
Method summary of creating deep learning model with keras/tensorflow 2.9
字符设备驱动程序之异步通知机制
DAMENG 用户管理
TypeScript-分布式条件类型
(transformation) tree, binary tree and forest transformation principle