当前位置:网站首页>LeetCode·每日一题·593.有效的正方形·数学
LeetCode·每日一题·593.有效的正方形·数学
2022-07-29 14:35:00 【小迅想变强】
链接:https://leetcode.cn/problems/valid-square/solution/by-xun-ge-v-ct2g/
来源:力扣(LeetCode)
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。
题目

示例

思路
解题思路
感觉在写初中数学题。。。。。。。
题目需要我们判断任意四点是否为正方形,先得知道正方形的基本判定定理:
- 对角线互相垂直平分且相等的四边形是正方形。
- 邻边相等且有一个内角是直角的平行四边形是正方形。
- 有一组邻边相等的矩形是正方形。
- 有一个内角是直角的菱形是正方形。
- 对角线相等的菱形是正方形。
- 对角线互相垂直的矩形是正方形。
- 有三个内角为直角且有一组邻边相等的四边形是正方形。
判别正方形的一般顺序:先说明它是平行四边形;再说明它是菱形(或矩形);最后说明它是矩形(或菱形)。
具体实现
先将四个点之间的长度求出,求任意两点之间的距离公式为

两点之间距离,可以不开根号,因为我们保持所有长度的比较都是带平方的比较
当边长相等且对角线相等时可以判断为正方形,当然也可以用勾股定理判断任意两条边与对角线是否构成a^2+b^2=c^2,这里使用简单比较,四边相等可以判断为菱形,对角线相等可以判断为矩形,同时满足这两个条件的只有正方形 利用判定定理5
代码
long len(int a, int b){
return (long)(a*a + b*b);//两点之间距离的平方,可以不开根号,因为所有长度的比较都是带平方的
}
int cmp(const void *a, const void*b){
return *(long*)a - *(long*)b;
}
/*
*给定任意四个点判断是否为正方形
*/
bool validSquare(int* p1, int p1Size, int* p2, int p2Size, int* p3, int p3Size, int* p4, int p4Size){
long tmp[6];
tmp[0] = len(p1[0]-p2[0], p1[1]-p2[1]);
tmp[1] = len(p1[0]-p3[0], p1[1]-p3[1]);
tmp[2] = len(p1[0]-p4[0], p1[1]-p4[1]);
tmp[3] = len(p2[0]-p3[0], p2[1]-p3[1]);
tmp[4] = len(p2[0]-p4[0], p2[1]-p4[1]);
tmp[5] = len(p3[0]-p4[0], p3[1]-p4[1]);
qsort(tmp, 6, sizeof(long), cmp);//升序处理
if(tmp[0] == 0) return false;//其中有边长为0,说明有任意两个点重合了
if(tmp[0] == tmp[1] && tmp[0] == tmp[2] && tmp[0]== tmp[3] && tmp[4] == tmp[5]) return true;//当边长相等且对角线相等时可以判断为正方形,当然也可以用勾股定理判断任意两条边与对角线是否构成a^2+b^2=c^2,这里使用简单比较,四边相等可以判断为菱形,对角线相等可以判断为矩形,同时满足这两个条件的只有正方形 5. **对角线相等的菱形是正方形。**
return false;
}
作者:xun-ge-v
链接:https://leetcode.cn/problems/valid-square/solution/by-xun-ge-v-ct2g/
来源:力扣(LeetCode)
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。时间空间复杂度

边栏推荐
猜你喜欢

AVH部署实践 (一) | 在Arm虚拟硬件上部署飞桨模型
换掉 UUID,更快、更安全!

Introduction to several methods of making custom welcome interface on Weiluntong touch screen

arcgis中编码方式改变引起的shp文件乱码、字符截断问题处理
代码越写越乱?那是因为你没用责任链

How to get local json

即时通讯-改变社交与工作状态的新型软件
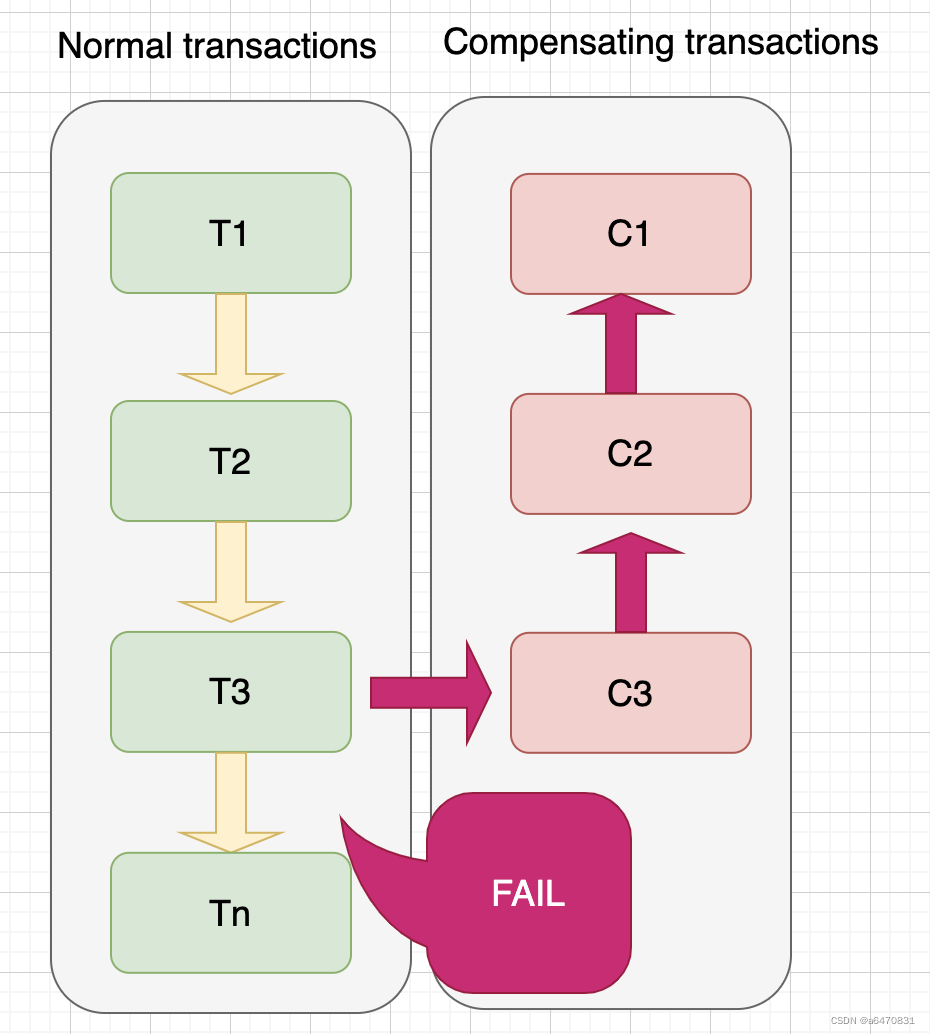
【微服务】(十六)—— 分布式事务Seata

Work Efficiency - Fifteen minutes allows you to quickly learn Markdown syntax to proficient in typesetting practice notes

QT通过UDP分包传输大图像(测试可传6M)
随机推荐
Offensive EA&UML day arch - activity diagram: : Variable Actions (continue)
全球级的分布式数据库 Google Spanner原理 热:报错
题目 1125: C语言训练-委派任务*
升级openssl1.1.1(mix2s哪个版本不断流)
《外太空的莫扎特》
超好用的PC端录屏软件推荐
QT通过UDP分包传输大图像(测试可传6M)
AC自动机笔记与例题整理
Domestic mobile phones turn users into their advertising broilers, no wonder consumers are buying iPhones
C语言 4:汇编语言指令介绍
MySQL 是如何实现 ACID 的?
即刻体验 | 借助 CTS-D 进一步提升应用设备兼容性
LeetCode_494_目标和
【C语言】AI三子棋的成长之路
部门例会上做测试分享,不知道分享什么内容?
一篇适合新手的深度学习综述!
Map遍历 key-value 的4种方法
MySQL Index Common Interview Questions (2022 Edition)
Nacos基础教程
AQS源码阅读与强软弱虚4种引用以及ThreadLocal原理与源码