当前位置:网站首页>运筹优化基础知识
运筹优化基础知识
2022-06-22 11:38:00 【百载文枢江左】
运筹优化基础知识
前言
本文为运筹优化基础知识总结,适合初学者或者经历了长时间搁置的读者。
线性规划模型的三种形式
LP模型有一般形式、规范形式和标准形式
一般形式
m i n z = c 1 x 1 + ⋯ + c n x n s . t . a i 1 x 1 + a i 2 x 2 + ⋯ + a i n x n = b i , i = 1 , ⋯ , p a i 1 x 1 + a i 2 x 2 + ⋯ + a i n x n ≥ b i , i = p + 1 , ⋯ , m x j ≥ 0 , j = 1 , ⋯ , q x j 无 限 制 , j = q + 1 , ⋯ , n min \quad z=c_1x_1+\cdots +c_nx_n \\ s.t.\quad a_{i1}x_1+a_{i2}x_2+\cdots +a_{in}x_n=b_i,i=1,\cdots ,p \\ \quad \quad a_{i1}x_1+a_{i2}x_2+\cdots +a_{in}x_n\geq b_i,i=p+1,\cdots ,m \\ x_j\geq 0,j=1,\cdots,q \\ x_j无限制,j=q+1,\cdots,n minz=c1x1+⋯+cnxns.t.ai1x1+ai2x2+⋯+ainxn=bi,i=1,⋯,pai1x1+ai2x2+⋯+ainxn≥bi,i=p+1,⋯,mxj≥0,j=1,⋯,qxj无限制,j=q+1,⋯,n
规范形式
m i n c T x s . t . A x ≥ b x ≥ 0 min\quad c^Tx\\ s.t. \quad Ax\geq b\\ \quad x\geq 0 mincTxs.t.Ax≥bx≥0
标准形式
m i n c T x s . t . A x = b x ≥ 0 min\quad c^Tx\\ s.t. \quad Ax= b\\ \quad x\geq 0 mincTxs.t.Ax=bx≥0
一般形式转换为规范形式,首先把
∑ j = 1 n a i j x j = b i \sum_{j=1}^n a_{ij}x_j=b_i j=1∑naijxj=bi
转换为
∑ j = 1 n a i j x j ≥ b i ∑ j = 1 n ( − a i j ) x j ≥ ( − b i ) \sum_{j=1}^n a_{ij}x_j\geq b_i\\ \sum_{j=1}^n (-a_{ij})x_j\geq (-b_i) j=1∑naijxj≥bij=1∑n(−aij)xj≥(−bi)
再用两个非负变量 x j + ≥ 0 x_j^+ \geq 0 xj+≥0和 x j − ≥ 0 x_j^- \geq 0 xj−≥0替代无符号限制变量
x j = x j + − x j − x_j = x_j^+ - x_j^- xj=xj+−xj−
一般形式转换为标准形式,首先把
∑ j = 1 n a i j x j ≥ b i \sum_{j=1}^n a_{ij}x_j\geq b_i j=1∑naijxj≥bi
转换为
∑ j = 1 n a i j x j − s i = b i , s i ≥ 0 \sum_{j=1}^n a_{ij}x_j - s_i= b_i,s_i\geq 0 j=1∑naijxj−si=bi,si≥0
其中 s i s_i si为剩余变量,也可以通过加松弛变量进行变换
无符号限制变量的转换同上
线性规划问题解的三种情况
- 可行区域 D = ∅ D=\varnothing D=∅,即该问题无解或不可行
- D ≠ ∅ D\neq \varnothing D=∅,但目标函数在D上无界,即该问题无界
- D ≠ ∅ D\neq \varnothing D=∅,且目标函数有有限的最优值,即该问题有最优解
凸集
凸集的定义:设 S ⊂ R n S\subset \bm{R}^n S⊂Rn是n维欧式空间中的一个点集,若对任何 x ∈ S , y ∈ S x \in S,y \in S x∈S,y∈S与任何的 λ ∈ [ 0 , 1 ] \lambda \in [0, 1] λ∈[0,1]都有
λ x + ( 1 − λ ) y ∈ S \lambda x+(1-\lambda)y \in S λx+(1−λ)y∈S
就称S是一个凸集
由凸集定义,易推到
D = { x ∈ R n ∣ A x = b , x ≥ 0 } D=\{x \in \bm{R}^n | Ax=b, x\geq0\} D={ x∈Rn∣Ax=b,x≥0}是凸集
任意多个凸集的交集还是凸集
对偶
自由变量对应等式约束
非负变量对应不等式约束
后续待补充
边栏推荐
- 机器学习与深度学习 --- 激活函数(未完待续)
- "Dare not doubt the code, but have to doubt the code" a network request timeout analysis
- HMS core news industry solution: let technology add humanistic temperature
- When the tiflash function is pushed down, it must be known that it will become a tiflash contributor in ten minutes
- Call center terminology
- APM flight mode switching -- source code explanation
- In C # development, the third-party components lambdaparser, dynamicexpresso and z.expressions are used to dynamically parse / evaluate string expressions
- 报错:unresolved variable $bus 及 “TypeError: Cannot read property ‘$on‘ of undefined“
- CF751E Phys Ed Online
- Macro definition usage and typedef and Const
猜你喜欢

《梦华录》成吸金王:广告主投500万排不上队,腾讯视频赢麻了?
![[2206] An Improved One millisecond Mobile Backbone](/img/75/b040f4b88050937dee57003b62f7b0.png)
[2206] An Improved One millisecond Mobile Backbone

SPI 与 API的区别

Typical life cycle model of information system project
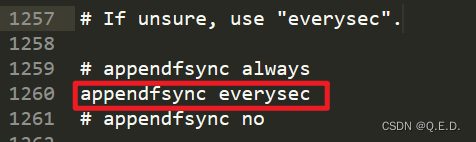
Redis - 9、持久化之AOF(Append OnlyFile)

Foreign lead needs energy, interest, research, diligence and is indispensable
【高频笔试题】513. 找树左下角的值

Redis - 4、新的3种数据类型

Matlab的KNN分类使用(附源码),实现像素分类(自己设置训练集比例),打印测试精度

迪利克雷前缀和学习笔记
随机推荐
Redis - 11、集群(Cluster)
Solution to 54e of Niuke challenge
Call center terminology
Redis - 9、持久化之AOF(Append OnlyFile)
Add custom fields to the time synchronization message based on uavcan protocol in Px4 code learning
鉴权之cookie、session、JWT
Redis - 7. Transaction operation
Typical life cycle model of information system project
Redis - 10. Master slave replication
机器学习与深度学习 --- 激活函数(未完待续)
Reader case of IO
Redis - 7、事务操作
Solution to 57c of Niuke challenge
Bytestream case of IO
"Dare not doubt the code, but have to doubt the code" a network request timeout analysis
maxscale在mariadb主从切换后如何处理event的状态-handle_events
迪利克雷前缀和学习笔记
关于缓存异常:缓存雪崩、击穿、穿透的解决方案
Noun analysis: ETL
Utilisation de la classification knn de Matlab (avec code source), réalisation de la classification des pixels (auto - réglage de l'échelle de l'ensemble de formation), précision de l'essai d'impressi