当前位置:网站首页>【剑指offer】——16.数值的整数次方
【剑指offer】——16.数值的整数次方
2022-08-03 02:56:00 【努力学习的少年】
- 个人主页:努力学习的少年
- 🤟 版权: 本文由【努力学习的少年】原创、在CSDN首发、需要转载请联系博主
- 如果文章对你有帮助、欢迎关注、点赞、收藏(一键三连)和订阅专栏哦
一. 题目
1.题目描述
实现 pow(x, n) ,即计算 x 的 n 次幂函数(即,x^n)。不得使用库函数,同时不需要考虑大数问题。
示例1
输入:x = 2.00000, n = 10
输出:1024.00000
示例2:
输入:x = 2.00000, n = -2
输出:0.25000
解释:2-2 = 1/22 = 1/4 = 0.25提示:
-100.0 < x < 100.0-2^31 <= n <= 2^31-1-104 <= xn <= 104
2.基础框架
class Solution {
public:
double myPow(double x, int n) {
}
};3.原题链接
二.解题报告
1.思路
我们将n用二进制的方式进行看待,例如,10 把它看成1010。定义一个变量a,如果二进制的32位中某个位中1的对应的 十进制是m,那么a=x^m.例如:1010 中的第2位的1表示2,m=2,a=x^2,1010 中的第4位的 1 十进制是8,则 m=8,a=x^8;定义一个变量res,表示结果值,从1到31遍历n的二进制位,如果其中位置为1,则 res*=a,在让a*=a, a则跳到下一个二进制位。如果n是负数,则将n取绝对值,按照步骤1,2,3计算res,最后在返回1/res。因为 -2^31 <= n <= 2^31-1,如果 n==-2^31,则不能将 -2^31 取绝对值,因为 n的正数的最大值是 2^31-1,为了防止这种情况出现,可以将所有n为负数+1,最后返回的时候多除个x即可,1/res/x;
如下:
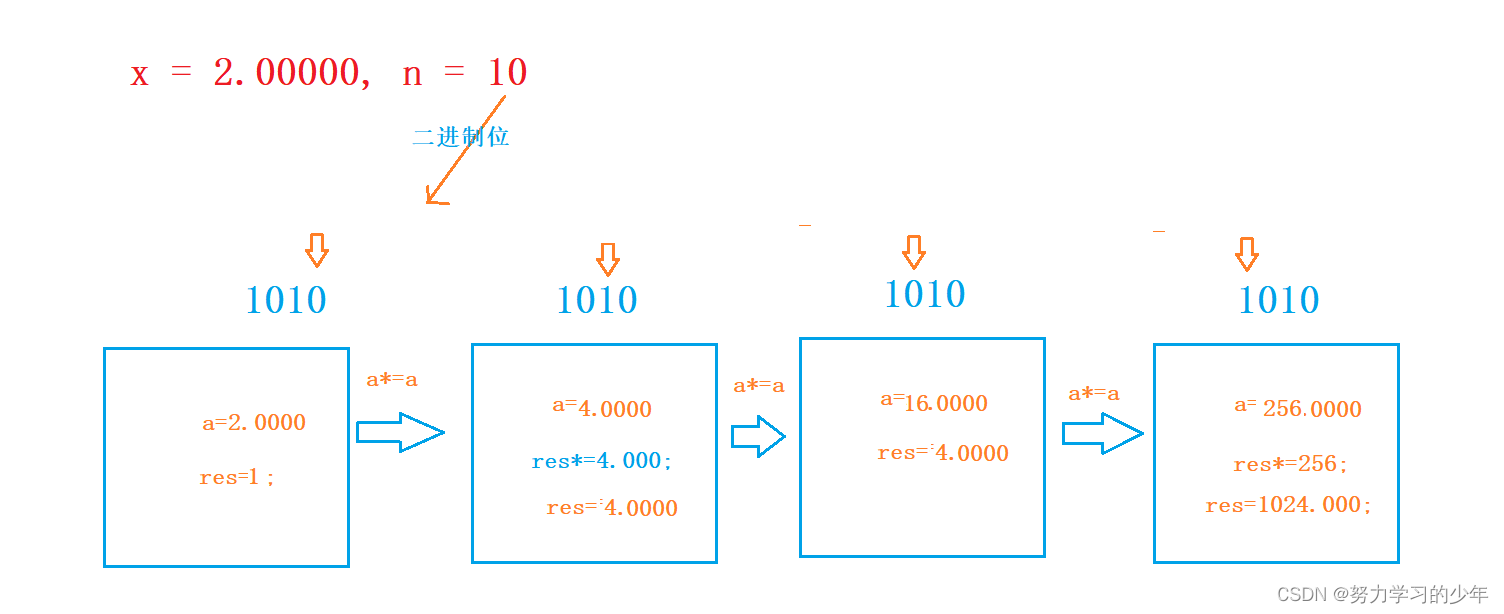
2.代码详解
class Solution {
public:
double myPow(double x, int n) {
int flag=1;//flag为1是正数,-1是负数
if(n<0){
//如果n小于0,则将其转变为正数
//如果n=2^-31,那么取绝对值还是2^-31,因为正数只能取到2^31-1
n=abs(n+1);
flag=-1;
}
double a=x;
double res=1;
while (n){
if(n&1){
//对应的二进制位是1
res*=a;
}
a*=a;
n>>=1;
}
if(flag==-1){
res=(1/res)/x;
}
return res;
}
};边栏推荐
猜你喜欢
随机推荐
ClickHouse—入门
IPv4编址;A类、B类、C类、D类、E类IP地址(IP地址;网络地址和主机地址;子网掩码;网关;广播地址;)
【obs】启动推流失败 : Output.StartStreamFailed 调用流程
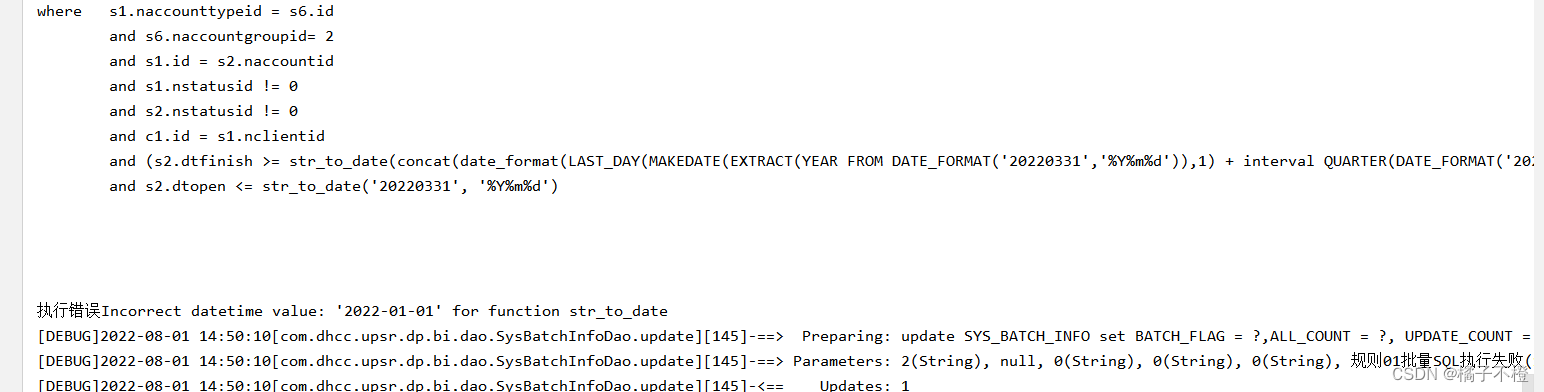
Incorrect datetime value: '2022-01-01' for function str_to_date
Jenkins2.328+sonarqube7.9 实现代码自动化检测
征集 |《新程序员》专访“Apache之父”Brian Behlendorf,你最想问什么?
370万欧元!西班牙iPronics加速可重构光子芯片商用
Likou second week wrong questions collection
leetcode:163 缺失的区间
els 结束判断
【Objective-C语言中的@property增强】
Pro_07丨波动率因子3.0与斜率因子
【UE4】搭建局域网内VR直播 UE4.27
【云原生】阿里云ARMS业务实时监控
问题记录:jenkins构建时报错The goal you specified requires a project to execute but there is no POM in...
Scala基础【异常、隐式转换、泛型】
Topic Modeling of Short Texts: A Pseudo-Document View
WordPress博客问答小插件
Incorrect datetime value: ‘2022-01-01‘ for function str_to_date
【原创】Auto.js get和post 案例