当前位置:网站首页>51. reverse order pairs in the array
51. reverse order pairs in the array
2022-06-12 05:20:00 【Be your goat】
The finger of the sword Offer 51. Reverse pairs in arrays
Ideas : Merge sort
- Termination conditions :l>=r when , return 0
- Recursive partition : Calculate the midpoint of the array m, Recursively divide the left subarray and the right subarray ;
- Merge and reverse pair Statistics :
- Temporary array nums Closed interval [l,r] To auxiliary array tmp
- Cyclic merger : Set the double pointers to point to the first element of the right sub array respectively :
- When i==m+1 when , Represents that the left sub array has been merged , Add right subarray , And implement j++
- otherwise , When j==r+1 perhaps tmp[i]<=tmp[j] when , Represents that the right sub array has been merged or the current element of the left sub array is smaller than the current element of the right sub array , Add the left sub array and execute i++
- otherwise , When tmp[i]>tmp[j] when , Represents that the current element of the left sub array is greater than the current element of the right sub array , Add the right sub array and execute j++, At this time, the reverse order pair is formed m-i+1, Add to res
- Merge and reverse pair Statistics :
- return res
class Solution {
public:
int reversePairs(vector<int>& nums) {
vector<int> tmp(nums.size());
int res=mergeSort(0,nums.size()-1,nums,tmp);
return res;
}
int mergeSort(int l,int r,vector<int>& nums,vector<int>& tmp){
if(l>=r) return 0;
int m=l+r>>1;
int res=mergeSort(l,m,nums,tmp)+mergeSort(m+1,r,nums,tmp);
for(int i=l;i<=r;++i) tmp[i]=nums[i];
int i=l,j=m+1,k=l;
while(k<=r){
if(i==m+1)
nums[k++]=tmp[j++];
else if(j==r+1||tmp[i]<=tmp[j]){
nums[k++]=tmp[i++];
}
else{
nums[k++]=tmp[j++];
res+=m-i+1;
}
}
return res;
}
};
Time complexity O(nlogn)
Spatial complexity O(n)
边栏推荐
- Day17 array features array boundary array application traversal array multidimensional array creation and traversal arrays operation array bubble sort
- Ray. Tune visual adjustment super parameter tensorflow 2.0
- Some optimization methods for UI Application of Qt5 on Hisilicon security platform
- Walking "daily question" and "DP"
- Why is Julia so popular?
- [GIS tutorial] land use transfer matrix
- [GIS tutorial] ArcGIS for sunshine analysis (with exercise data download)
- 31. stack push in and pop-up sequence
- Caused by: org. h2.jdbc. JdbcSQLSyntaxErrorException: Table “USER“ already exists; SQL statement:
- The server time zone value ‘Ö Ð¹ ú±ê ×¼ ʱ ¼ ä‘ is unrecognized or represents more than one time zone. You
猜你喜欢

Harris corner detection principle-

National land use data of 30m precision secondary classification

Soil type, soil texture, soil nutrient and change data, soil organic matter, soil pH, soil nitrogen, phosphorus and potassium

Servlet core technology

C asynchronous programming (async and await) and asynchronous method synchronous invocation

Quickly get PCA (principal component analysis) (principle code case)

Qinglong wool - Kaka

Some problems of Qinglong panel

Normalized vegetation index (NDVI) data, NPP data, GPP data, evapotranspiration data, vegetation type data, ecosystem type distribution data
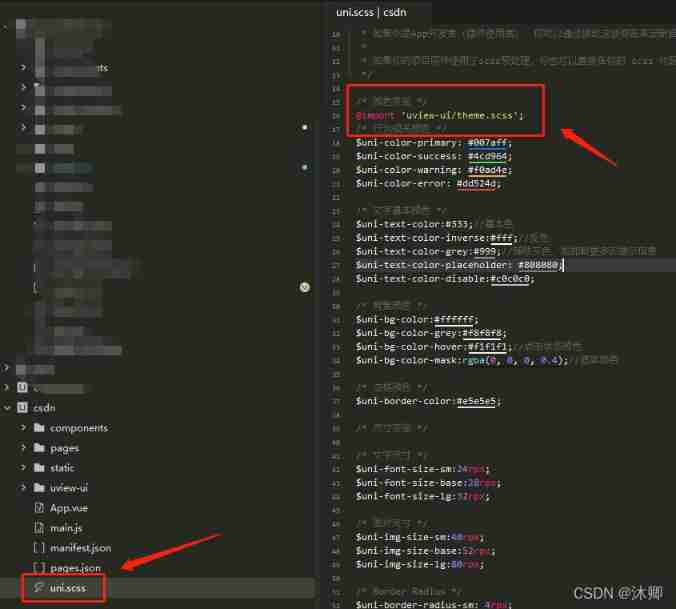
How to quickly reference uview UL in uniapp, and introduce and use uviewui in uni app
随机推荐
Main business objects of pupanvr record (5)
How to count the total length of roads in the region and draw data histogram
加速訓練之並行化 tf.data.Dataset 生成器
Qs100 at command mqtt access thingsboard
Yolo opencv scale identification scale reading identification water gauge identification water level identification source code
Thingsboard view telemetry data through database
Three. JS import model demo analysis (with notes)
Walking "daily question" and "DP"
Ray. Tune visual adjustment super parameter tensorflow 2.0
Pupanvr- an open source embedded NVR system (1)
Summary of problems in rv1109/rv1126 product development
National land use data of 30m precision secondary classification
Acquisition of Lai data, NPP data, GPP data and vegetation coverage data
Pupanvr hardware and software board side development environment configuration (4)
JS to determine whether it is the first time to browse the web page
[backtracking method] backtracking method to solve the problem of Full Permutation
Radiometric calibration and atmospheric correction of sentry 2 L1C multispectral data using sen2cor
Introduction to MMS memory optimization of Hisilicon MPP service
Sword finger offer30 days re brush
SQL transaction