当前位置:网站首页>零知识证明:具有DDH假设的 ZKP
零知识证明:具有DDH假设的 ZKP
2022-07-28 17:06:00 【chinadefi】
零知识证明:具有DDH假设的 ZKP


Diffie-Hellman部分
我们必须证明我们仍然持有一个秘密(私有)密钥,这是一个非常典型的情况。那我们怎么把Victor和Peggy绑定到一个证明基础设施中让Peggy向Victor证明她还持有一把私钥呢?为此,我们将通过交换Diffie-Hellman密钥来绑定Victor和Peggy。
在DDH中,我们有一个由 * g、ga*、*gb、g^{ab }* 组成的元组,其中a和b是秘密。ga和gb的值在双方交换后,应该都能生成g^{ab}:

Chaum-Pedersen部分
如果Peggy是证明者,而Victor是验证者,那么Peggy需要表明她知道一个秘密值a。有了Chaum-Pedersen ZKP,Victor让Peggy生成一个ZKP来保护一个秘密。在这个过程中,她将g^a (mod p)的值发送给Victor,当Victor需要证明她仍然知道一个值时,他将发送一个挑战值(s),然后Alice生成一个随机值,并返回y_1=gr和y_2=Br。然后Victor检查gz=A^s y_1 (mod p)和Bz=Cs y_2 (mod p)是否相等。

在Victor和Peggy交换他们的秘密后,Victor将持有g^a (mod p), Peggy将持有g^b(mod p)。对于零知识证明,我们这样开始:

Peggy有一个秘密值a并生成A = g^a。Victor 的秘密值为b并生成B = g^b。他们交换A和B,然后使用 Diffie Hellman 方法生成C。
Victor向Peggy发送一个commitment:

Peggy计算出一个随机值:

她发给Victor:

和:

Peggy还发送:

Victor会检查:

和:

如果这些都是真的,那么Peggy已经证明她知道这个秘密(a)。因为:

代码
代码如下所示:
import random
import libnum
import sys
bitsize=128
if (len(sys.argv)>1):
bitsize=int(sys.argv[1])
p=libnum.generate_prime(bitsize)
s=random.getrandbits(bitsize)
g=2
a=random.getrandbits(bitsize)
b=random.getrandbits(bitsize)
c=random.getrandbits(bitsize)
r=random.getrandbits(bitsize)
A=pow(g,a,p)
B=pow(g,b,p)
C=pow(g,a*b,p)
y1=pow(g,r,p)
y2=pow(B,r,p)
z=(r+a*s) % (p-1)
print("== Chaum-Pederson ZKP with DDH ==")
print("p=",p)
print("a=",a)
print("A=g^a (mod p)=",A)
print("b=",b)
print("B=g^a (mod p)=",B)
print("ab=",a*b)
print("C=g^{ab} (mod p)=",C)
print("\nProof: g^z = A^s y1")
val1= pow(g,z,p)
val2=(pow(A,s,p)*y1) % p
print("Val1=",val1)
print("Val2=",val2)
if (val1==val2):
print("- Proof verified")
print("\nProof: B^z = C^s y2")
val3= pow(B,z,p)
val4=(pow(C,s,p)*y2) % p
print("Val3=",val3)
print("Val4=",val4)
if (val3==val4):
print("- Proof verified")
256位素数的运行示例如下:
== Chaum-Pederson ZKP ==
p= 71808837207067558396943502247178805470599306337269585872075038503116361400603
a= 36623398984913964172485596625205226031763309121917034188846578869320021978402
A=g^a= 32096207796582799691444233880948982714496908564580085529419678203181985482397
b= 31626404664308059618102781249870451013488637545242770934698960204990436278054
B=g^a= 22868249499514124460303251323889043821880224466294750444534923941031732565838
ab= 1158266436479298052448345755868228483694002563526288816181771624565721107667448582344993414115064433575649547672009235534272667805336831732117954454589708
C=g^{ab}= 8021151953795073005899136029637476282156155200732630284950825682466003109726
Proof: g^z = A^s y1
Val1= 9590670516289397297344719778854690756344241363231213529959870845950311348445
Val2= 9590670516289397297344719778854690756344241363231213529959870845950311348445
- Proof verified
Proof: B^z = C^s y2
Val3= 56336209634019548929170814618015392124101293159018455662661735618180853220223
Val4= 56336209634019548929170814618015392124101293159018455662661735618180853220223
- Proof verified
结论
网络安全的唯一方向是零信任模式。阻止敏感信息数据泄露的一种方法不是储存这些秘密,而是用随机的预言机代替它们。即便这些预言机被泄漏,真正的秘密也不会被泄漏。在我概述的方法中,我们可以通过散列使用证明的生成值轻松地将其转换为 NI-ZKP(非交互式 ZKP)。
Source:https://medium.com/asecuritysite-when-bob-met-alice/hellman-pedersen-and-chaum-zkps-with-the-decisional-diffie-hellman-ddh-assumption-4ed7d4a3220d
关于
ChinaDeFi - ChinaDeFi.com 是一个研究驱动的DeFi创新组织,同时我们也是区块链开发团队。每天从全球超过500个优质信息源的近900篇内容中,寻找思考更具深度、梳理更为系统的内容,以最快的速度同步到中国市场提供决策辅助材料。
Layer 2道友 - 欢迎对Layer 2感兴趣的区块链技术爱好者、研究分析人与Gavin(微信: chinadefi)联系,共同探讨Layer 2带来的落地机遇。敬请关注我们的微信公众号 “去中心化金融社区”。

边栏推荐
- 腾讯汤道生:开源是产业互联网时代新的生产方式和协作模式
- Ue5 gas learning notes 1.9 skill system global classes (abilitysystemglobals)
- NDK series (5): from introduction to practice, JNI explodes the liver and explains everything in detail!
- .net swagger
- 专题讲座6 树形dp 学习心得(长期更新)
- Ue5 gas learning notes 1.8 game special effects (gameplaycue)
- LeetCode_ 63_ Different paths II
- Ue5 gas learning notes 1.6 skills gameplay ability
- redis优势以及数据结构相关知识
- Golang 并发之锁
猜你喜欢

Detailed explanation of oscilloscope probe

Live broadcast starrocks technology insider: low base global dictionary optimization

Detailed explanation of oscilloscope parameters

Detailed explanation of network RJ45 interface

Gateway入门

npm 无法将“npm”项识别为 cmdlet、函数、脚本文件或可运行程序的名称。请检查名称的拼写,如果包括路径,请确保路径正确,然后再试一次。

冒泡排序和相关视频

Introduction and advanced MySQL (4)

Shenzhen offline registration starrocks on AWS: how to conduct rapid unified analysis of real-time data warehouses
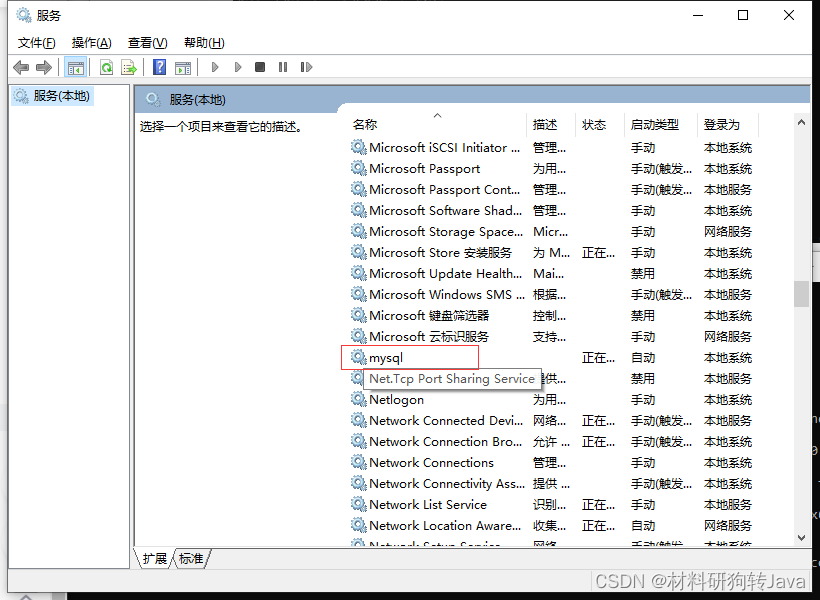
ERROR 2003 (HY000) Can‘t connect to MySQL server on ‘localhost3306‘ (10061)解决办法
随机推荐
Go语言系列之日志库zap
2022-07-27 第四小组 修身课 学习笔记(every day)
Redis缓存雪崩、穿透、击穿,布隆过滤器,分布式锁详解
十进制转二进制进阶版(可转化负数以及边界值)
How does Xiaobai learn software testing with zero foundation?
三分钟了解快来新媒体
苹果开发完整的苹果证书与描述文件创建流程
Detailed explanation of oscilloscope probe
Ue5 gas learning notes 0.2 configuration plug-in
Summer Challenge [FFH] JS custom component: DIY a keyboard that can be used at any time! (I)
Introduction and advanced level of MySQL (9)
MYSQL入门与进阶(五)
Go concurrency one
MongoDB数据库shell命令执行
冒泡排序和相关视频
ERROR 2003 (HY000) Can‘t connect to MySQL server on ‘localhost3306‘ (10061)解决办法
数字化洪流 :企业转型中的资源重组与战略冲突
Golang 并发之锁
LVS手册
2022.7.26 constructor, interview: the role of new, deep copy and shallow copy