Dynamic programming problem (4)

One 、 The minimum path sum of matrices

solution : Dynamic programming

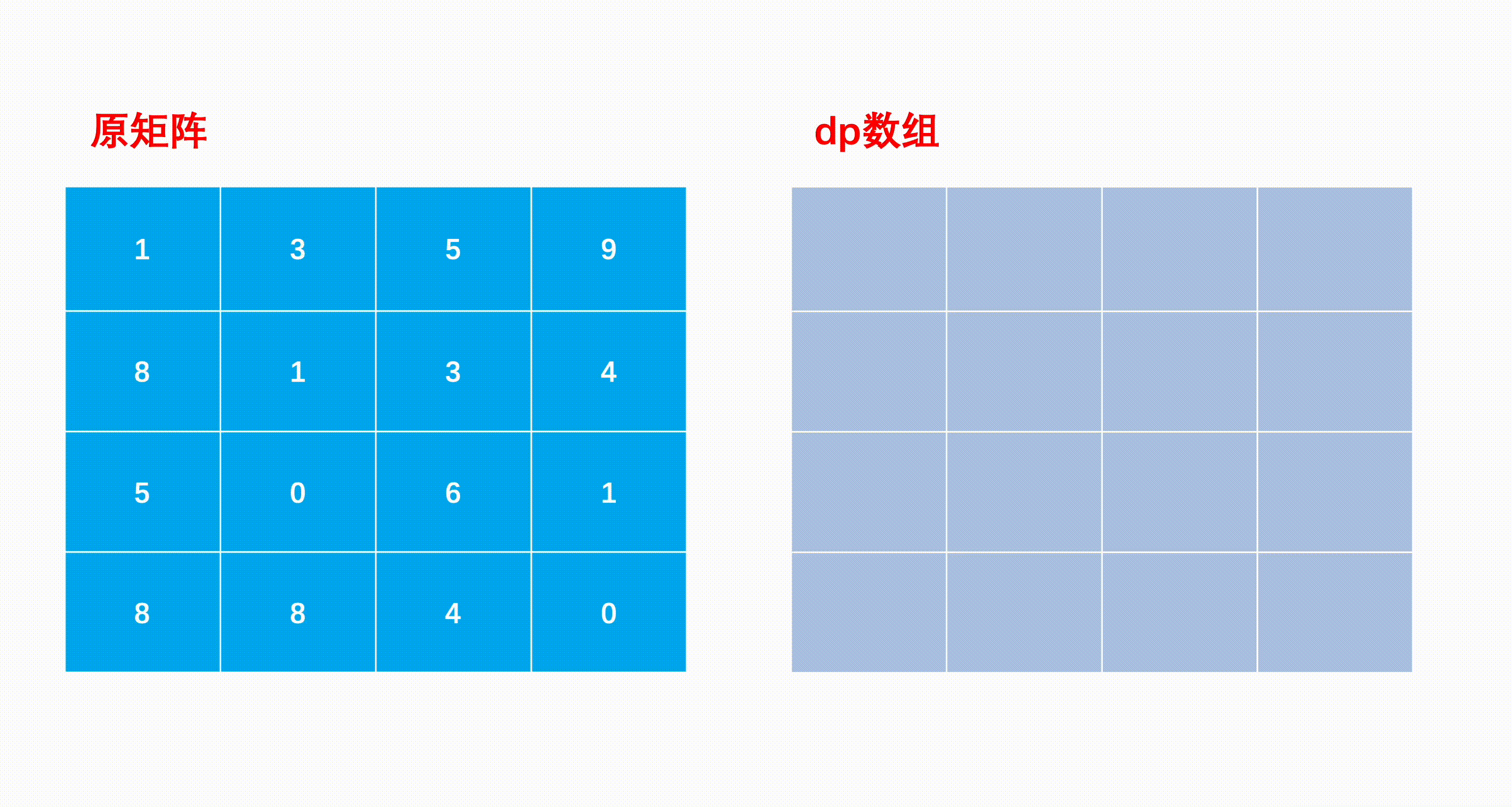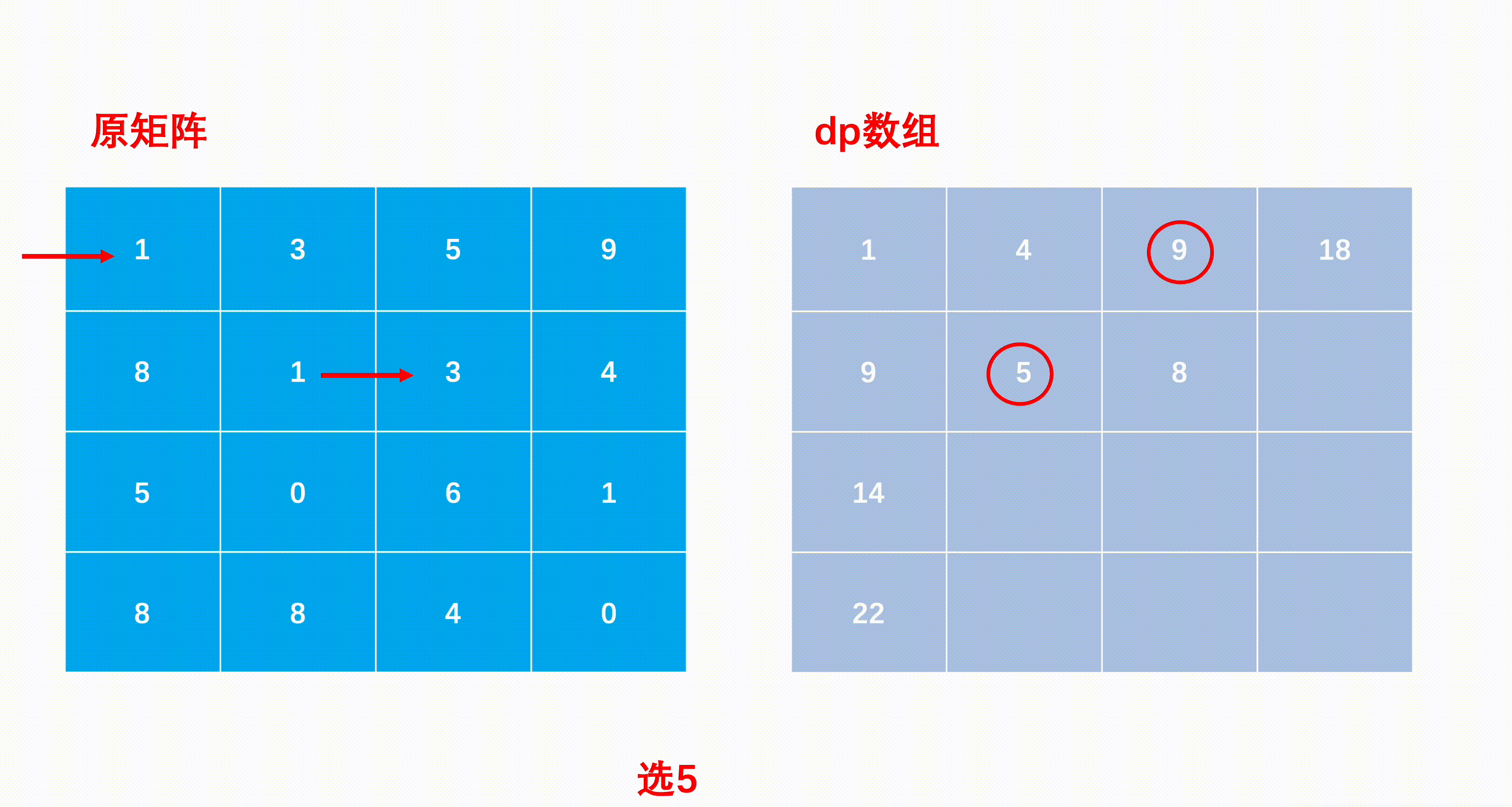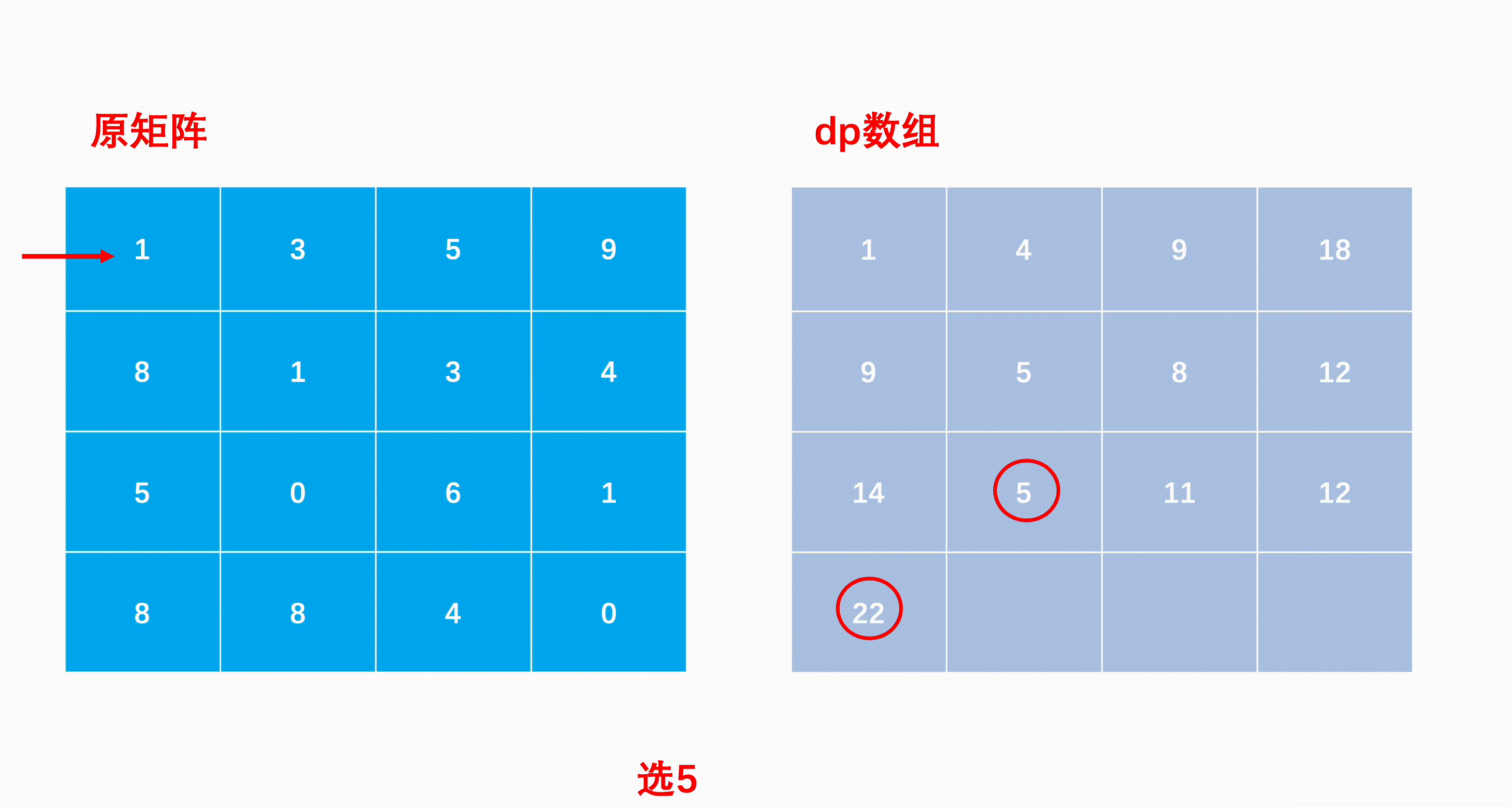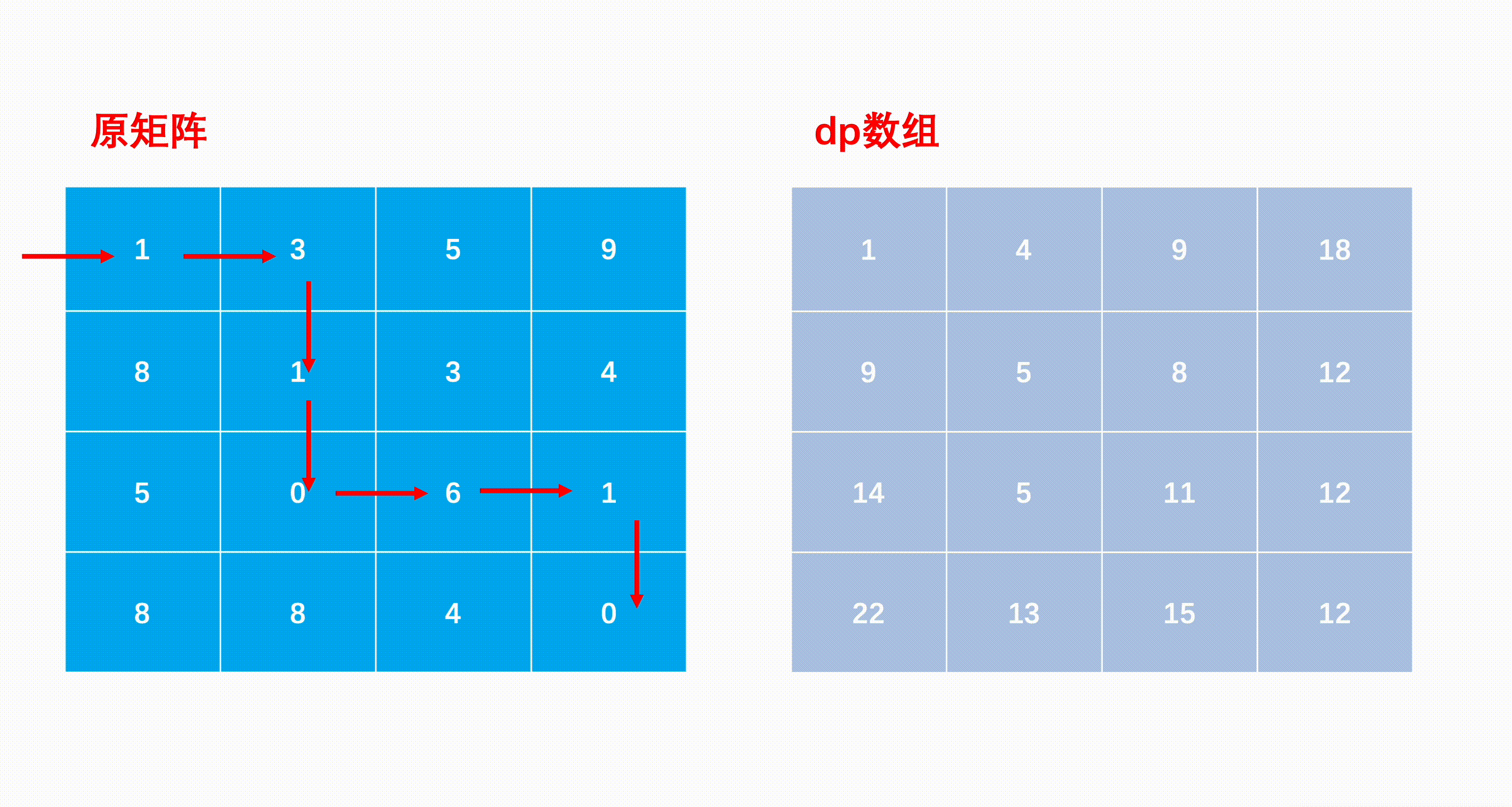
• We can construct a two-dimensional auxiliary array of the same size as the matrix , among dp[i][j] Said to (i,j) The shortest path whose position is the end point and , be dp[0][0]=matrix[0][0]
• It's easy to know the first row and the first column , Only right or down , There is no second option , So the first row can only be accumulated by the left side , The first column can only be accumulated by the above .
• After the edge state is constructed , ergodic matrix , Complete each position in the matrix dp Array value ： If the current position is (i,j), The last step is either (i−1,j) Down , Either it's (i,j−1) To the right , Then the sum of the smaller value and the value of the current position is the minimum path to the current position , So the state transition formula is dp[i][j]=min(dp[i−1][j],dp[i][j−1])+matrix[i][j]
• Last move to (n−1,m−1) The position of is the shortest path to the lower right corner and
  

class Solution {
    
public:
    int minPathSum(vector<vector<int> >& matrix) {
    
        int n = matrix.size();
        // because n,m Are greater than or equal to 1
        int m = matrix[0].size();  
        //dp[i][j] Express with current i,j The shortest path length with the position as the end point 
        vector<vector<int> > dp(n + 1, vector<int>(m + 1, 0));
        dp[0][0] = matrix[0][0];
        // Process the first column 
        for(int i = 1; i < n; i++)
            dp[i][0] = matrix[i][0] + dp[i - 1][0];
        // Deal with the first line 
        for(int j = 1; j < m; j++)
            dp[0][j] = matrix[0][j] + dp[0][j - 1];
        // Others follow the formula 
        for(int i = 1; i < n; i++){
     
          for(int j = 1; j < m; j++){
    
              dp[i][j] = matrix[i][j] + (dp[i - 1][j] > dp[i][j - 1] ? dp[i][j - 1] : dp[i - 1][j]);
          }
      }
       return dp[n - 1][m - 1];
    }
};

Time complexity ：O(mn), Traverse the row and column of the matrix separately , Then traverse the entire matrix
Spatial complexity ：O(mn), auxiliary metrix dp It's a two-dimensional array

Two 、 Translate numbers into strings

solution : Dynamic programming

• Use auxiliary array dp Before presentation i How many decoding methods are there .
• For a number , We can decode it directly , It can also be compared with the previous 1 perhaps 2 Combine to decode ： If you decode directly , be dp[i]=dp[i−1]; If combined decoding , be dp[i]=dp[i−2].
• There is only one decoding method , Select a species dp[i−1 that will do , For satisfying two decoding methods （10,20 You can't ） It is dp[i−1]+dp[i−2]
• Add... In turn , final dp[length]] That's the answer .

class Solution {
    
public:
    int solve(string nums) {
    
        // exclude 0
        if(nums == "0")  
            return 0;
        // There is only one possibility of exclusion 10  and  20
        if(nums == "10" || nums == "20")  
            return 1;
        // When 0 It's not in front of 1 or 2 when , Unable to decode ,0 Kind of 
        for(int i = 1; i < nums.length(); i++){
      
            if(nums[i] == '0')
                if(nums[i - 1] != '1' && nums[i - 1] != '2')
                    return 0;
        }
        // Auxiliary array initialized to 1
        vector<int> dp(nums.length() + 1, 1);  
        for(int i = 2; i <= nums.length(); i++){
    
            // stay 11-19,21-26 The situation between 
            if((nums[i - 2] == '1' && nums[i - 1] != '0') || (nums[i - 2] == '2' && nums[i - 1] > '0' && nums[i - 1] < '7'))
               dp[i] = dp[i - 1] + dp[i - 2];
            else
                dp[i] = dp[i - 1];
        }
        return dp[nums.length()];
    }
};

Time complexity ：O(n), Both iterations are single-layer
Spatial complexity ：O(n), Auxiliary array dp

3、 ... and 、 Change money ( One )

Solution 1 : Dynamic programming ( recommend )

• It can be used dp[i] Means to make up i Yuan requires the minimum amount of money .
• It is set to the maximum value at the beginning aim+1, So the currency is the smallest 1 element , That is, the number of currencies will not exceed aim
• initialization dp[0]=0.
• Subsequent traversal 1 Yuan to aim element , Enumerate the possible composition of each denomination of currency , Take the minimum value of each time , The transfer equation is dp[i]=min(dp[i],dp[i−arr[j]]+1)
• Last comparison dp[aim] Whether the value of exceeds aim, If more than that, there is no solution , Otherwise, you can return .

class Solution {
    
public:
    int minMoney(vector<int>& arr, int aim) {
    
        // Less than 1 All return 0
        if(aim < 1) 
            return 0;
        //dp[i] Means to gather together i What is the minimum amount of money required for yuan 
        vector<int> dp(aim + 1, aim + 1);  
        dp[0] = 0; 
        // Traverse 1-aim element 
        for(int i = 1; i <= aim; i++){
     
            // Each denomination of currency should be enumerated 
            for(int j = 0; j < arr.size(); j++){
     
                // You can only use it if the face value does not exceed the amount you need to raise 
                if(arr[j] <= i) 
                    // Maintenance minimum 
                    dp[i] = min(dp[i], dp[i - arr[j]] + 1); 
            }
        }
        // If the final answer is greater than aim Represents no solution 
        return dp[aim] > aim ? -1 : dp[aim]; 
    }
};

Time complexity ：O(n⋅aim), The first layer traverses the enumeration 1 Yuan to aim element , The second layer traverses the enumeration n The face value of each currency
Spatial complexity ：O(aim), Auxiliary array dp Size

Solution 2 : Spatial memory recursion

For the need to make up aim The money , For the first time, we can choose to use arr[0], Then we need to figure out aim−arr[0] The money , Then the following is the sub problem of the previous one , Recursion can be used . Because the use of each denomination is not limited , So for the first time we can use arr Every one in the array , Similarly, it can also be used every time arr Every time in the array , So every recursion must traverse arr Array , It is equivalent to that the branch is arr.size() Tree recursion .

• Recursion , Once the remaining money is 0, Then find a situation , Record the total amount of money used , Maintain the minimum value .
• Once the remaining money needs to be scraped up, it is negative , It means that this branch has no solution , return -1.
• You can also use it every time later arr Once in the array , Enter sub problem .
• But the complexity of tree recursion needs O(aim^n), Too much double counting , As shown in the figure , So we can use a dp Array records the result of each recursion , Avoid double counting of small branches , If dp You can get the array value directly , No more double counting .

class Solution {
    
public:
    int recursion(vector<int>& arr, int aim, vector<int>& dp){
    
        // The combination exceeds , return -1
        if(aim < 0) 
            return -1;
        // The combination is just equal to the change needed 
        if(aim == 0) 
            return 0;
        // Whether the remaining change has been calculated 
        if(dp[aim - 1] != 0) 
            return dp[aim - 1];
        int Min = INT_MAX;
        // Traverse all the values 
        for(int i = 0; i < arr.size(); i++){
     
            // Recursive operation selects the current face value 
            int res = recursion(arr, aim - arr[i], dp); 
            // Get the minimum 
            if(res >= 0 && res < Min) 
                Min = res + 1;
        }
        // Update minimum 
        dp[aim - 1] = Min == INT_MAX ? -1 : Min; 
        return dp[aim - 1];
    }
    int minMoney(vector<int>& arr, int aim) {
    
        // Less than 1 All return 0
        if(aim < 1) 
            return 0;
        // Record the value in the middle of recursion 
        vector<int> dp(aim, 0); 
        return recursion(arr, aim, dp);
    }
};

Time complexity ：O(n⋅aim), All in all, we need to calculate aim The answer of three states , Each state needs to be enumerated n Par value
Spatial complexity ：O(aim), Recursive stack depth and auxiliary array space