数字IC设计中基本运算的粗略的延时估计

本文以与逻辑门电路为最小单位，对数字IC中的一些基本逻辑运算的延时进行了粗略的评估分析。

一、逻辑门电路的延时

由于一些材料的特性，将其做成与非门成本最低，因此很多设计的最底层将与非门作为最基本的元件。可以通过与非门来实现与，或，非，异或的运算。博客【1】对这部分有很详细的介绍，由于逻辑门电路搭建方式的不同，因此各个逻辑门之间的延时并没有确定的换算关系（查到了好几种），但基本上异或门运算的延时都大于与，或，非这种基础逻辑门的。

二、半加器

半加器的真值表如下所示：

in1	in2	sum	cout
0	0	0	0
0	1	1	0
1	0	1	0
1	1	0	1

由表可知，sum = in1^in2; cout = in1 & in2;

如图所示，由于异或门延时大于与门，因此，一个半加器的延时等于一个异或门的延时。

三、全加器

由图一个全加器可以由两个半加器组成，由于半加器的组成可知，count计算的延时为2个与门的延时和一个或门的延时，而sum计算的延时为2个异或门的延时。因此一个全加器的延时为2个异或门的延时，即1个全加器的延时为2个半加器的延时。

四、多个多位加法运算的延时估算

假设有assign a = a0 + a1 + a2; 其中a0为2bit，a1, a2为3bit。我们可以采用行波进位加法器的原理进行估算；

全加器搭建该加法运算的结构如上所示，其中FA为全加器，因此上图结构的延时为5个全加器的延时；以此类推，m个数的连续加法运算，若在不失真的情况下，运算结果为N bits，则延时为 N + m – 1个全加器的延时.

五、+1，+2，+4运算的延时估算

数字IC设计中常常需要用到+1运算，如果只是给某个变量+1，则不需要按上节的方式算，可以有更简单的方式。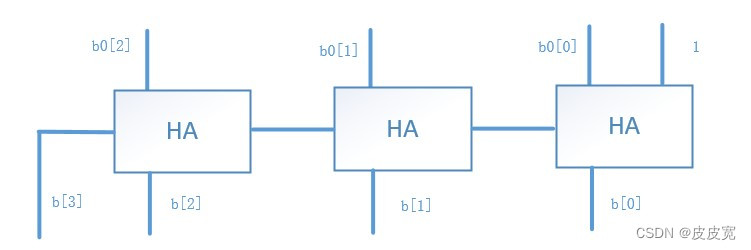

HA为半加器，如上图所示，Nbit变量的+1运算，只需要N个半加器的延时即可，即N/2个全加器的延时。同理，如果是Nbit变量的+2运算，假设out = in + 2，in为Nbit，则可以被看做out[N : 1] = in[N-1 : 1] + 1’b1; 和 out[0] = in[0]，因此，N bit变量+2运算的延时为(N-1)/2个全加器的延时。依此类推，N > m 时，N bits变量+2^m的延时为(N-m)/2个全加器的延时；

六、乘法器的延时估算

乘法器估算时，我们采用阵列乘法器的结构，假设 a为3 bit，b为2 bit的变量；则a * b的结构图为：

因此，依次类推，M bit * N bit运算的延时可以粗略的估计为M + N – 1个全加器的延时；（图中a0[12]应为a0[2]）；

七、 总结

本文只是根据电路的结构，对一些基本运算进行了粗略的估计，具体的延时换算还需要根据课本（考试），手册（项目）的具体要求来；

八、参考资料

【1】个人博客：通过 与非门 构建异或门
【2】CSDN：乘法器的实现（阵列、Booth、Wallace）
【3】CSDN：行波进位加法器设计
【4】CSDN：全加器和行波进位加法器的延迟时间