当前位置:网站首页>Zero-knowledge proof - zkSNARK proof system
Zero-knowledge proof - zkSNARK proof system
2022-08-04 20:02:00 【Looking Back at the White Speed Dragon King】
This notebook is excerpted from Steven Yue
Three core algorithms:
setup convention circuit, generate random parameters
prove: the prover generates a zero-knowledge proof
verify: the verifier verifies
Completeness: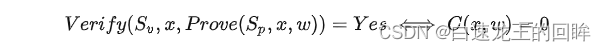
Proof of knowledge: (verykey)
Prove that the prover does have some information that we don't know, that is, this w does exist
Short Proof: Short and Efficient
Zero-Knowledge: Public input x and proof pi cannot reveal w
PCP Theorem (Probability Verifiable Theorem)
All NP-hard problems can be proved by random sampling by random verification methods
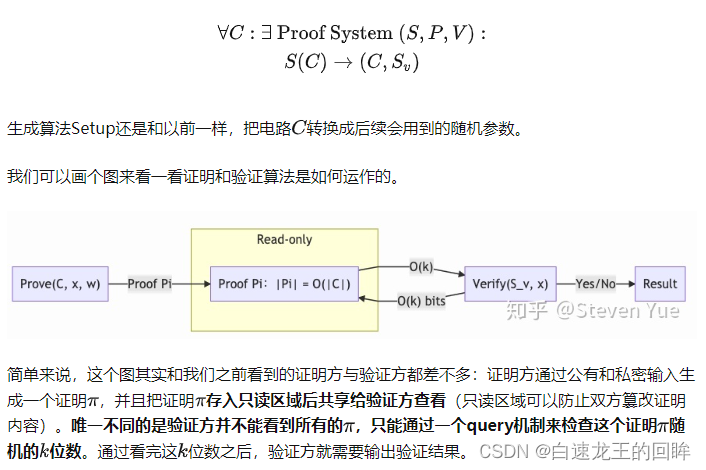
Instead of looking directly at pi, it can only be extracted from itk-bit
In general, it is a random check. The more correct the random check, the lower the possibility of fraud (a bit of a hypothesis test)
Kilian SNARK
PCP may have huge read-only storage area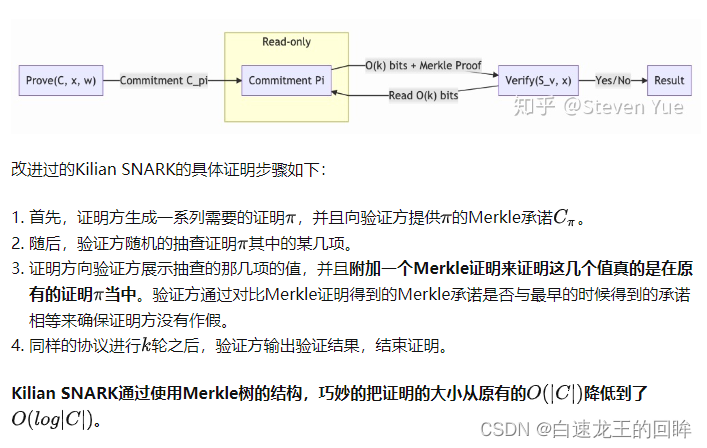
We will program a commitment in readonly
The prover only needs to attach a Merkle Proof to prove that the data submitted by himself is indeed in the pi when displaying the data
This can avoid storing a large amount of pi information
Non-Interactive Killian SNARK
The verifier does not need to be online when the prover submits the proof, it can verify at random events later
Requires Fiat-Shamir-Heuristic, which can convert any interactive random verification protocol into a non-interactive one
First we need a secure hash function H (random oracle, no matter what the input is, the output value can be regarded as a random number that is not associated with the input) 
The key to the transformation is to rely on the random value of the authenticator to generate a secure hash function
LCPC (Linear)
Two polynomials with different coefficients of order d will only have at most d points coincident
By treating the proved value as the coefficient of the polynomial, and then verifying whether the value of the polynomial at a certain point is equal


So we convert SNARK into polynomial form
But it is difficult for the circuit to become polynomial form, so we need aThe program matrix called R1CS

Polynomial interpolation, Vandermonde polynomial, restores eachA coefficient
Construct into polynomials P, Q, R
Prove that P * Q = R
Summary
PCP theorem is to quickly verify the solution of any NP problem by random sampling method.
LPCP is a constrained version of PCP, which describes the method of quickly verifying the coefficients of polynomials by randomly checking the values of polynomials.
Fiat-Shamir Heuristic can turn an interactive protocol into a non-interactive protocol.
Starting from a mathematical operation circuit, after transforming into an R1CS program matrix, it can be finally restored to a polynomial
边栏推荐
猜你喜欢

搭建MyCat2一主一从的MySQL读写分离
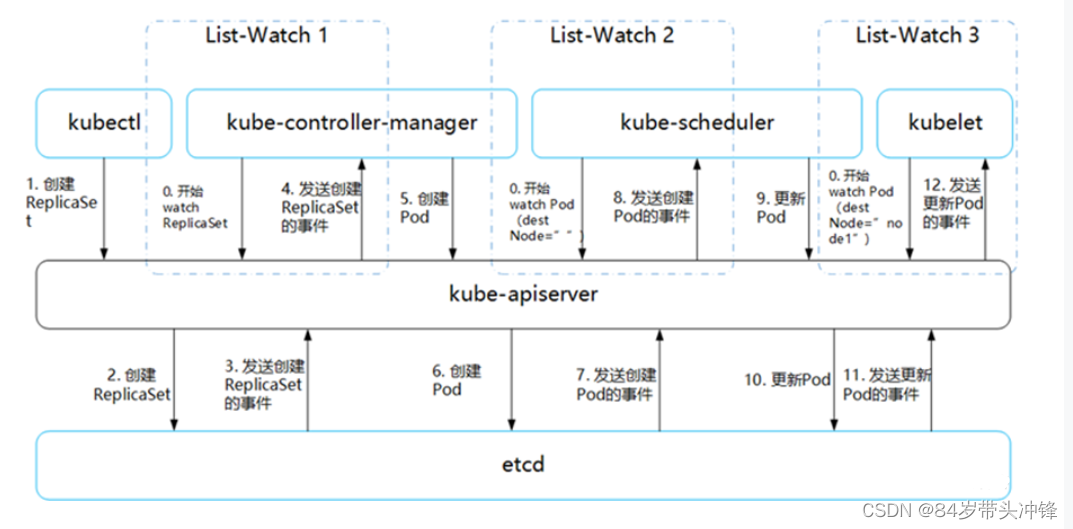
The list of Kubernetes - watch mechanism

Ant Group's time series database CeresDB is officially open source

In July 2022, domestic database memorabilia

新式茶饮,卷完水果还能卷什么?
【着色器实现Glitch单项故障闪烁效果(与Television效果不同)_Shader效果第十四篇】

「 WAIC 2022 · 黑客马拉松」蚂蚁财富两大赛题邀你来战!

基于Nodejs的电商管理平台的设计和实现
C#弹出询问对话框
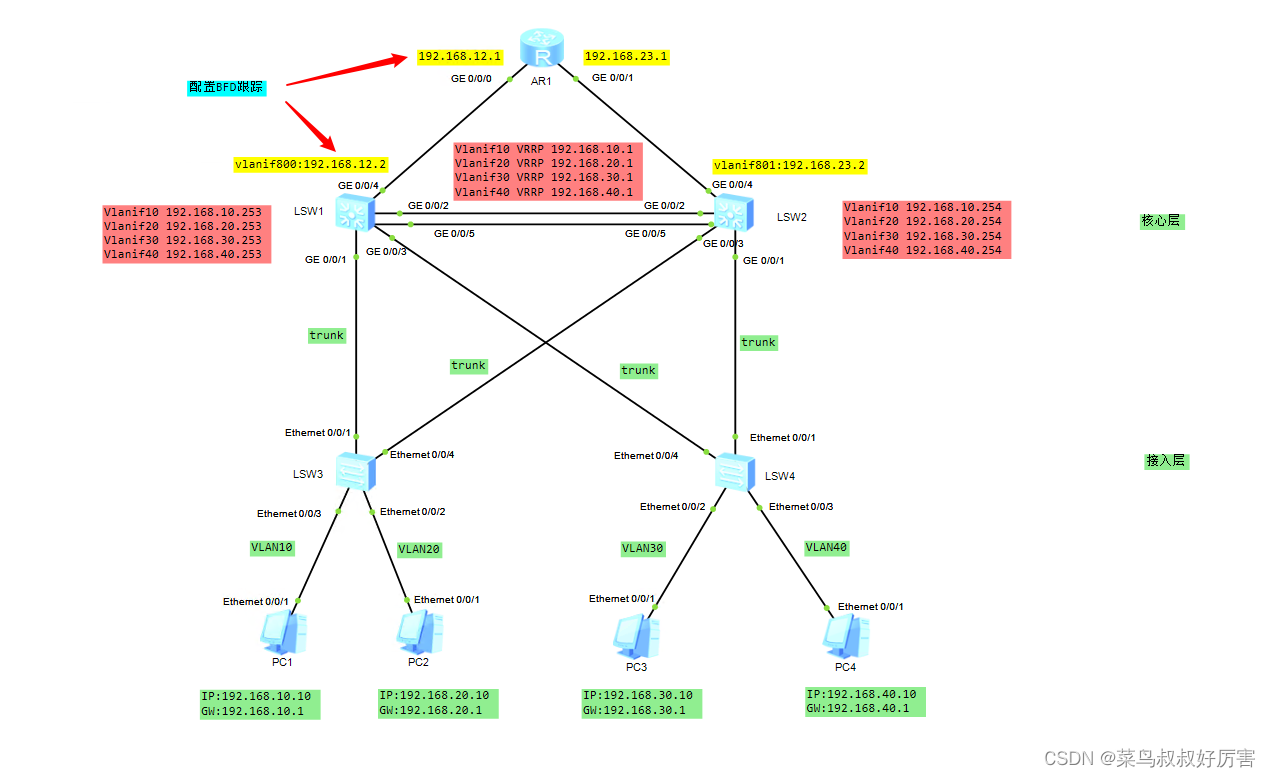
华为企业组网实例:VRRP+MSTP典型组网配置
随机推荐
Chrome安装zotero connector 插件
阿里的arthas使用,入门报错:Unable to attach to 32-bit process running under WOW64
vs Code 运行一个本地WEB服务器
How to monitor code cyclomatic complexity by refactoring indicators
jMeter Thread group 对应的 constant timer
SAP UI5 确保控件 id 全局唯一的实现方法
多商户商城系统功能拆解22讲-平台端分销商品
lds链接的 顺序问题
zynq 记录
MYSQL gets the table name and table comment of the database
电脑一键重装系统内存完整性无法打开怎么办
Apache服务器配置多个站点
「 WAIC 2022 · 黑客马拉松」蚂蚁财富两大赛题邀你来战!
前3名突然变了,揭秘 7 月编程语言最新排行榜
nr部分计算
If it is test axi dma catch a few words here
力扣题(5)—— 最长回文子串
图片延迟加载、预加载
华为企业组网实例:VRRP+MSTP典型组网配置
刷题-洛谷-P1307 数字反转