当前位置:网站首页>Mathematical problems (number theory) trial division to judge prime numbers, decompose prime factors, and screen prime numbers
Mathematical problems (number theory) trial division to judge prime numbers, decompose prime factors, and screen prime numbers
2022-07-02 04:52:00 【Wu Yu 4】
Prime number
In more than 1 In the integer of , Only 1 And itself , It's called prime number ( Prime number ).
1. The judgment of prime number ( Trial division )
int prime(long long n)
{
if(n<2) return 0;// Greater than required 1 The positive integer
else
{
for(int i=2;i<n;i++)// Go through it , The time complexity is appropriate O(n) Overtime
{
if(n%i==0) return 0;
}
}
return 1;
}Optimize it :
because n/d=x, meanwhile n/x=d It was also established , So we can conclude that divisors exist in pairs .
So we just need to enumerate the smaller one , namely d<=n/d, Rewrite the cycle condition as i<=n/i, In this way, the time complexity is O(sqrt(n)) 了 .
Topic link :866. Try division to determine the prime number - AcWing Question bank
Topic :
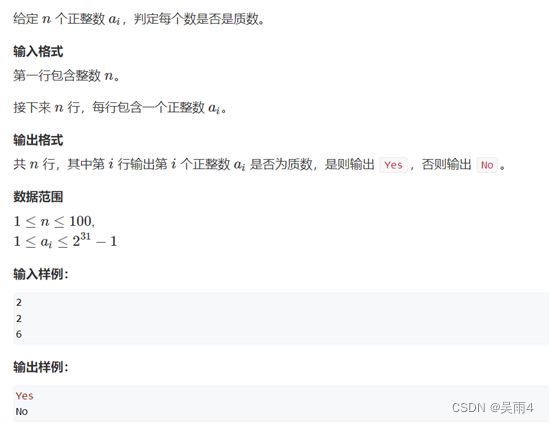
2. Decomposing prime factor ( Trial division )
Prime factor refers to the prime factor that can divide a given division .
【 If there are only two numbers 1 A common qualitative factor , Called coprime 】
【1 And any positive integer are mutually prime numbers 】
【 Any number can be regarded as the multiplication of multiple prime factors ,n=p1^k1*p2^k2*…*pn^kn】
link :AcWing 867. Decomposing prime factor - AcWing
Topic :
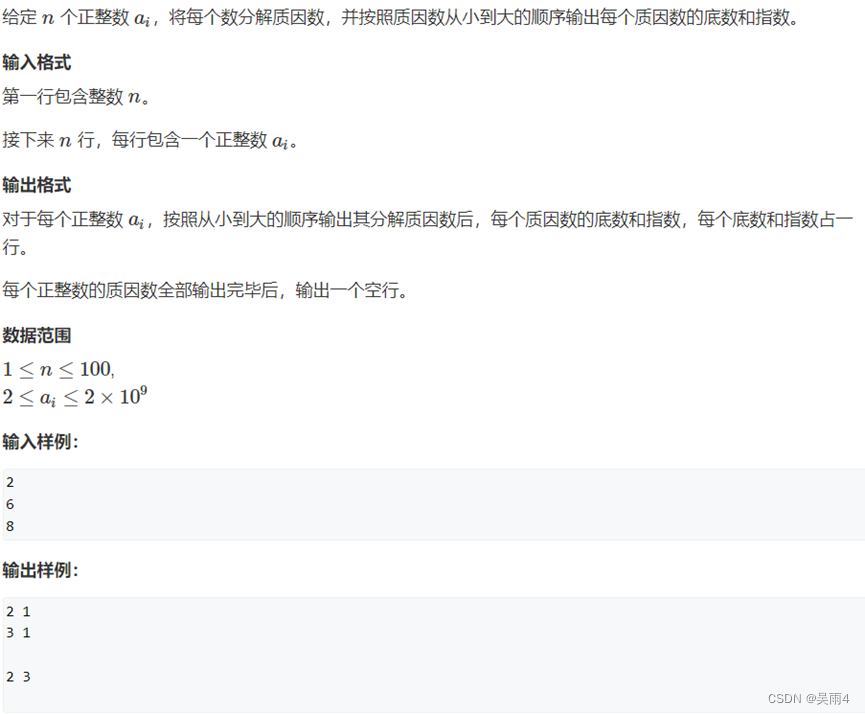
Code :
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
int main()
{
ios::sync_with_stdio(false);
cin.tie(0);
cout.tie(0);
ll t;
cin>>t;
while(t--)
{
ll n;
cin>>n;
for(int i=2;i<=n;i++)// The time complexity is O(n), Timeout
{
if(n%i==0)// What seems to be found is n The factor of , Not prime factor .
/* But there's no problem here , Because once the following is found, it can be divisible i,n Will enter the cycle until i Until you know you can't get rid of it . take 4 An example to , stay i=2 When n/=2 ——>n=2, also n/=2——>n=0. No, i=4 What's the matter , So divide all the cases where the factors are composite numbers , Guarantee that they are prime factors .*/
{
int s=0;
while(n%i==0)// Find out the index
{
n/=i;
s++;
}
cout<<i<<" "<<s<<endl;
}
}
cout<<endl;// The output has the requirement that each data should be wrapped
}
return 0;
}
Optimize it :
because n At most one of them is greater than sqrt(n) The quality factor of
So the cycle condition is changed to i<=n/i, At the same time, add a special judgment if(n>1) cout<<n<<" "<<1<<endl;
Code :
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
int main()
{
ios::sync_with_stdio(false);
cin.tie(0);
cout.tie(0);
ll t;
cin>>t;
while(t--)
{
ll n;
cin>>n;
for(int i=2;i<=n/i;i++)// The time complexity is O(sqrt(n)), At most sqrt(n)
{
if(n%i==0)
{
int s=0;
while(n%i==0)
{
n/=i;
s++;
}
cout<<i<<" "<<s<<endl;
}
}
if(n>1) cout<<n<<" "<<1<<endl;
cout<<endl;
}
return 0;
}
3. Sieve prime number

Topic link :868. Sieve prime number - AcWing Question bank
Topic :
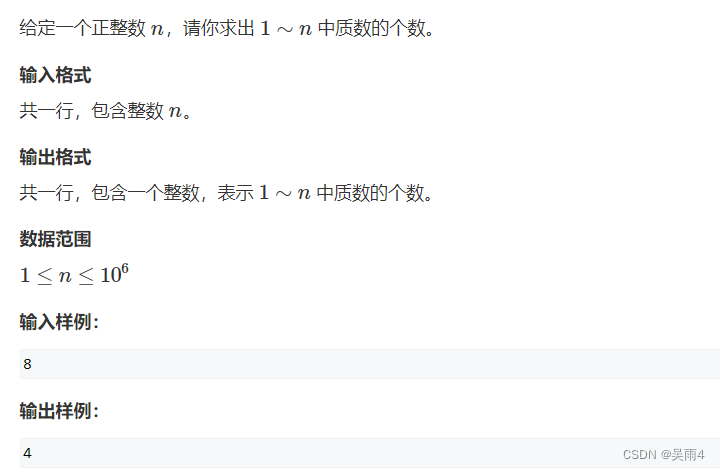
Code :
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N=1e6+10;
int primes[N],cnt,n;
bool st[N];
int main()
{
cin>>n;
for(int i=2;i<=n;i++)
{
if(!st[i])// Traverse prime numbers from small to large , The smallest is 2
primes[cnt++]=i;
for(int j=i+i;j<=n;j+=i)// hold i All multiples of are deleted
st[j]=true;
}
cout<<cnt<<endl;
return 0;
}Time complexity calculation :
n/2+n/3+n/4+…+n/n
=n(1/2+1/3+1/4+…+1/n)
When n Towards positive infinity , The following is harmonic series , The value is ln n+c (c by 0.57)
Again because ln n<log2 n
So the time complexity is :O(nlog2 n)
Optimize it : Put the second cycle into if Go inside , Namely Ethmoidal method
Specific Ehrlich screen conveyor gate :
Code :
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N=1e6+10;
int primes[N],cnt,n;
bool st[N];
int main()
{
ios::sync_with_stdio(false);
cin.tie(0);
cout.tie(0);
cin>>n;
for(int i=2;i<=n;i++)
{
if(!st[i])// Traverse prime numbers from small to large , The smallest is 2
{
primes[cnt++]=i;
for(int j=i+i;j<=n;j+=i)// hold i All multiples of are deleted
st[j]=true;
}
}
cout<<cnt<<endl;
return 0;
}

Both times AC, But the second sieve is five times faster than the first .
There is another kind. Linear sieve method :( The data range is 1e7 when It is twice as fast as Ehrlich sieve )
Code :
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N=1e6+10;
int primes[N],cnt,n;
bool st[N];
int main()
{
ios::sync_with_stdio(false);
cin.tie(0);
cout.tie(0);
cin>>n;
for(int i=2;i<=n;i++)
{
if(!st[i])// Traverse prime numbers from small to large , The smallest is 2
primes[cnt++]=i;
for(int j=0;primes[j]<=n/i;j++)
{
st[primes[j]*i]=true;
if(i%primes[j]==0) break;
}
}
cout<<cnt<<endl;
return 0;
}
边栏推荐
- Unit testing classic three questions: what, why, and how?
- 解析少儿编程中的动手搭建教程
- 面试会问的 Promise.all()
- C# 基于MQTTNet的服务端与客户端通信案例
- CY7C68013A之keil编译代码
- Let genuine SMS pressure measurement open source code
- oracle 存储过程与job任务设置
- C language practice - number guessing game
- Application d'un robot intelligent dans le domaine de l'agroécologie
- idea自動導包和自動删包設置
猜你喜欢

解析少儿编程中的动手搭建教程
Summary of common string processing functions in C language

Unity particle Foundation
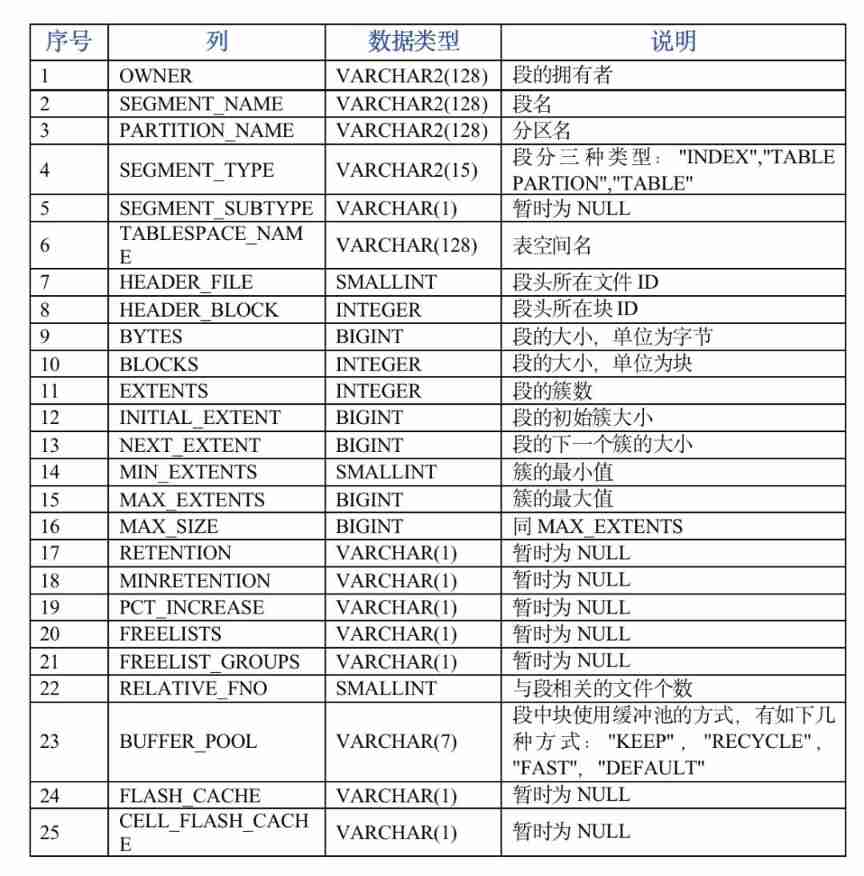
Analyze the space occupied by the table according to segments, clusters and pages
Let正版短信测压开源源码

正大留4的主账户信息汇总

What data does the main account of Zhengda Meiou 4 pay attention to?

Unit testing classic three questions: what, why, and how?

Steam教育的实际问题解决能力
Thinkphp內核工單系統源碼商業開源版 多用戶+多客服+短信+郵件通知
随机推荐
奠定少儿编程成为基础学科的原理
Ognl和EL表达式以及内存马的安全研究
Mapping location after kotlin confusion
Federal learning: dividing non IID samples according to Dirichlet distribution
The solution to the complexity brought by lambda expression
How to recover deleted data in disk
What methods should service define?
缓存一致性解决方案——改数据时如何保证缓存和数据库中数据的一致性
Virtual machine installation deepin system
TypeScript类的使用
One step implementation of yolox helmet detection (combined with oak intelligent depth camera)
Analyze the space occupied by the table according to segments, clusters and pages
Thinkphp内核工单系统源码商业开源版 多用户+多客服+短信+邮件通知
Future trend of automated testing ----- self healing technology
二叉树解题(一)
面试会问的 Promise.all()
The core idea of performance optimization, dry goods sharing
C# 基于MQTTNet的服务端与客户端通信案例
DC-1靶场搭建及渗透实战详细过程(DC靶场系列)
Starting from the classification of database, I understand the map database