Realizing deep learning framework from zero -- LSTM from theory to practice [theory]

introduction

In line with “ Everything I can't create , I can't understand ” Thought , This series The article will be based on pure Python as well as NumPy Create your own deep learning framework from zero , The framework is similar PyTorch It can realize automatic derivation .

Deep understanding and deep learning , The experience of creating from scratch is very important , From an understandable point of view , Try not to use an external complete framework , Implement the model we want . This series The purpose of this article is through such a process , Let us grasp the underlying realization of deep learning , Instead of just being a switchman .

What we introduced earlier is simple RNN There are some problems , That is, it is difficult to keep the information away from the current position and the gradient disappears .

LSTM

LSTM Designed to solve the above problems . By making the network learn to forget unwanted information , And remember the information you need to make decisions in the future , To explicitly manage contextual information .

LSTM The context management problem is divided into two sub problems ： Remove information that is no longer needed from the context , And adding information that is more likely to be needed for future decisions .

framework

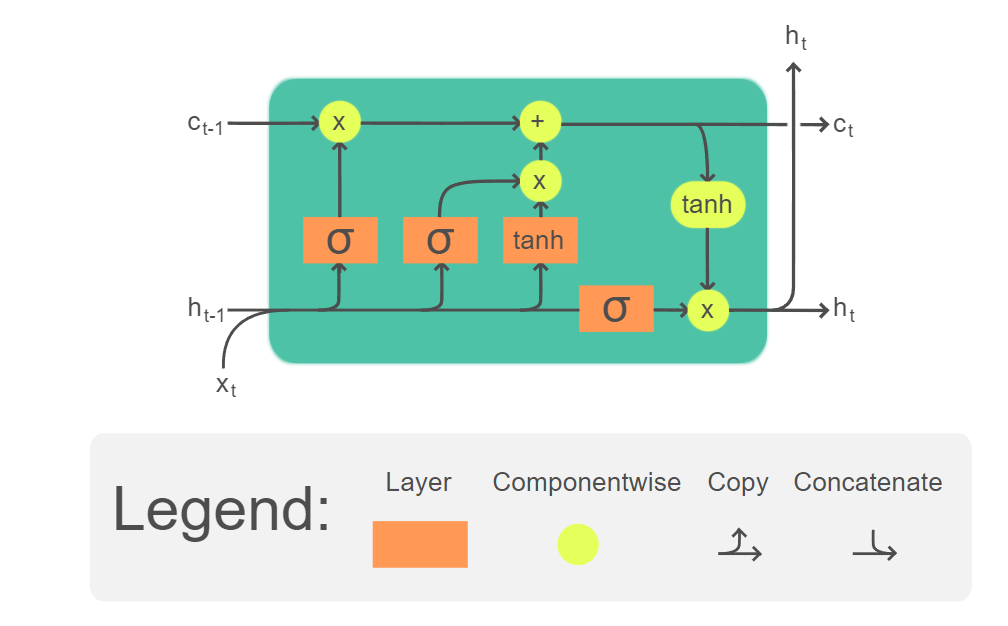
The key to solving these two problems is to learn how to manage this context , Instead of hard coding policies into the architecture .LSTM First Add a display context layer to the network ( Except for the common RNN Hidden layer ), And by using specialized neurons , Gates are used to control the flow of information into and out of the units that make up the network layer . These gates are used through the input 、 Additional weight operations are added to the previous hidden state and the previous context state respectively .

LSTM These doors in share the same design pattern ： Each contains a feedforward network , Next is sigmoid Activation function , Finally, there is an element level multiplication with the gated layer .

choice sigmoid As an activation function, its output is based on 0 To 1 Between . The effect combined with element level multiplication is similar to binary mask (binary mask). Close to the mask 1 The values in the gate layer corresponding to the values of are almost the same ; The value corresponding to the lower value is basically erased .

Oblivion gate

The first door we introduced is the forgetting door (forget gate). The purpose of this gate is to delete information that is no longer needed by the context . The forgetting gate calculates the weighted sum of the previous hidden state and the current input , And pass sigmoid convert . obtain mask, The mask Then it is multiplied by the context vector element level to remove the context information that is no longer needed .

$$f_t=\sigma (U_f{h}_{t-1}+W_f{x}_t)\text{\hspace{1em}(1)}$$
among $U_f$ and $W_f$ Is two weight matrices ;$h_{t-1}$ For the previous hidden state ;$x_t$ Enter... For the current ;$\sigma$ by sigmoid function , Here we ignore the bias term .

$$k_t=c_{t-1}\odot f_t\text{\hspace{1em}(2)}$$
among $c_{t-1}$ Represents the previous context layer vector ; Element level multiplication of two vectors ( By operator $\odot$ Express , Sometimes called Hadamard product ) Is the multiplication of the corresponding elements of two vectors .

The forgetting gate controls the context vector in memory $c_{t-1}$ Whether to be forgotten .

Input gate

Similarly , The input gate also passes through the previous hidden state $h_{t-1}$ And current input $x_t$ Calculation ：
$$i_t=\sigma (U_i{h}_{t-1}+W_i{x}_t)\text{\hspace{1em}(3)}$$
Then we calculate the previous hidden state $h_{t-1}$ And current input $x_t$ Extract actual information from —— all RNN The basic operations used by the network ：
$$g_t=\tanh (U_g{h}_{t-1}+W_g{x}_t)\text{\hspace{1em}(4)}$$
In a simple RNN in , The result of the above calculation is the hidden state of the current time , But in LSTM Middle is not .LSTM The hidden state in is based on the context state $c_t$ Calculated .
$$j_t=g_t\odot i_t\text{\hspace{1em}(5)}$$

Multiply the input gate to control $g_t$( Also known as candidate values ) How much can be stored in the current context state $c_t$.

We put what we got above $j_t$ and $k_t$ Add it up to get the current context state $c_t$：
$$c_t=j_t+k_t\text{\hspace{1em}(6)}$$

Output gate

The last gate is the output gate , It is used to control which information of the current hidden state is needed .
$$o_t=\sigma (U_o{h}_{t-1}+W_o{x}_t)\text{\hspace{1em}(7)}$$

$$h_t=o_t\odot \tanh (c_t)\text{\hspace{1em}(8)}$$

Given the weights of different gates ,LSTM Accept the context layer and hidden layer of the previous time and the current input vector as input . then , It generates updated context vectors and hidden vectors as output . Hidden layer $h_t$ Can be used as a stack RNN Input of subsequent layers in , Or generate output for the last layer of the network .

For example, based on the current hidden state , You can calculate the output at the current time ${\hat{y}}_t$：
$${\hat{y}}_t=\text{softmax}(W_y{h}_t+b_y)\text{\hspace{1em}(9)}$$

All in all ,LSTM Calculation $c_t$ and $h_t$.$c_t$ Long term memory ,$h_t$ Short term memory . Use input $x_t$ and $h_{t-1}$ Renew long-term memory , In update , some $c_t$ The characteristics of the forgotten gate $f_t$ eliminate , Some other features have been added from the input gate to $c_t$ in .

The new short-term memory is the long-term memory process $\tanh$ Multiplied by the output gate . Be careful , On update ,LSTM Not looking at long-term memory $c_t$. Only modify it .$c_t$ And never go through a linear transformation . This is why the gradient vanishes and explodes .

References

1. Speech and Language Processing