【C语言】夏日一题 —— 求最大公约数和最小公倍数

作者:凡人编程传
系列:夏日一题 — 刷题专栏
说明:这个夏天，带你逆袭！

前言

hello!这是我们这一系列的开篇章哦！这一节先带你们吃两个小菜，后面我们慢慢来吃大货哦！持续关注夏日一题系列哦！

最大公约数

• 法一

给定两个数，求他们的最大公约数。两个数的最大公约数是不可能超过其中较小数的，可以试想一下假设求24与18的最大公约数，那么他们的最大公约数最大就是18把(这里这是假设),这个最大公约数是不可能比18大的，因为若超过了18是不能约分的，所以我们就确定了一个范围。这时候我们就可以假设18这个数是一个极限，然后看他是否可以同时整除18和24，若不是18自减,依次来穷举可以同时整除18和24的，这时候就可以求到最大公约数了。

代码如下:

#include<stdio.h>
int main()
{
    
int m, n;
printf("请输入两个整数:>");
scanf("%d%d", &m, &n);
int max = m < n ? m : n;		//假设最大公约数(最大公约数一定不超过两个数的较小数)
while (1)
{
    
	if (m % max == 0 && n % max == 0)		//满足能同时整除两个数
	{
    
		printf("最大公约数是:%d", max);
		break;
	}
	max--;		//若较小数不是最大公约数，就自减了穷举
}
return 0;
}

测试j结果: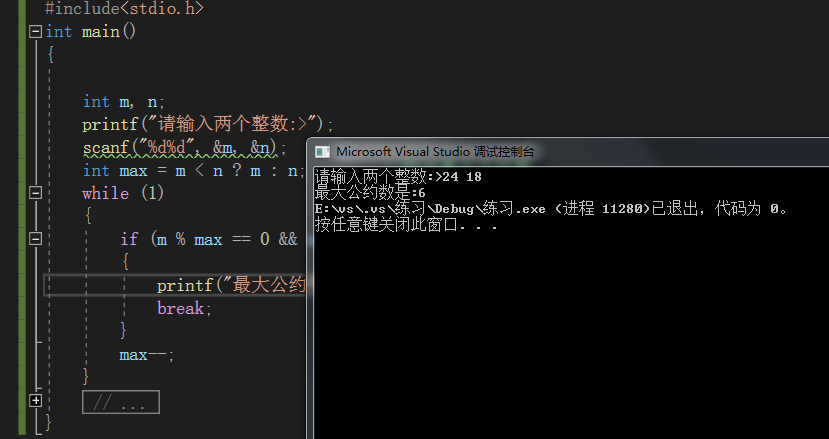

• 法2
  这个方法来自于数学的辗转相除法，也就是将两个数取模然后把第一余数替代原除数,作为除数，原来的除数替代原被除数,作为被除数。然后再进行取模，第二余数作为替代第一余数作为被除数,第一余数又替代原除数，作为被除数。知道两个数取模为0时，那个除数就是最大公约数.

举例如图:

有的人会担心如果m>n怎么办，18%24还是商0余18，所以进行m=n,n=r后。自动调回m=24,n=18了

代码如下:

#include<stdio.h>
int main()
{
    
	int m, n;
	printf("请输入两个整数:>");
	scanf("%d%d", &m, &n);
	int r = 0;
	while (m % n)				//辗转相除法求最大公约数
	{
    
		r = m % n;
		m = n;
		n = r;
	}
	printf("最大公约数:%d\n", n);
	return 0;
}

测试j结果: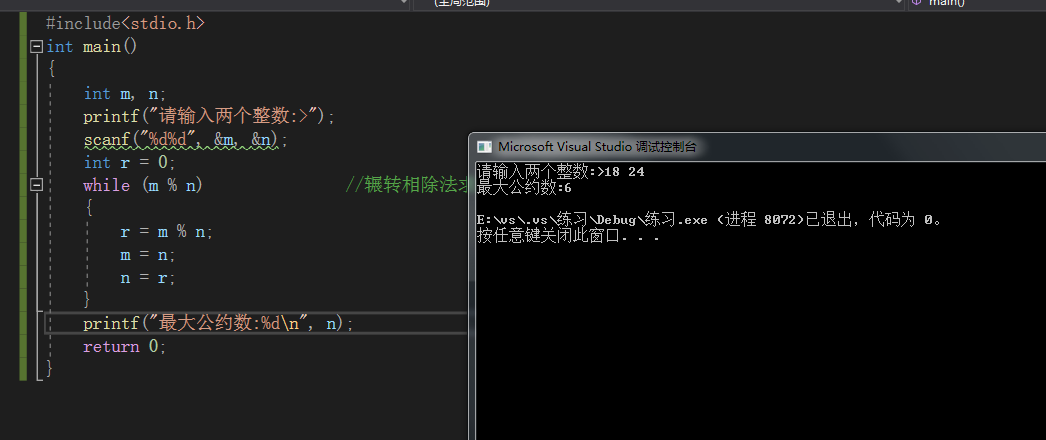

最小公倍数

• 法一

同求最大公约数的法一，两个数的小公倍数最小也是两个数的较大数的倍数,这时候也可以假设最小公倍数最小是两个数较大数，若不是就自增来穷举找到可以同时整除。如24与18，最小公倍数一定是不小于24的，如果是18，那练24的一倍都不是。所以就确定了一个范围由此来穷举即可。

代码如下:

#include<stdio.h>
int main()
{
    
	int m, n;
	printf("请输入两个整数:>");
	scanf("%d%d", &m, &n);
	int min = m > n ? m : n;		//假设最小公倍数
	while (1)
	{
    
		if (min % m == 0 && min % n == 0)
		{
    
			printf("最小公倍数是:%d",min);
			break;
		}
		min++;
	}
	return 0;
}

测试结果: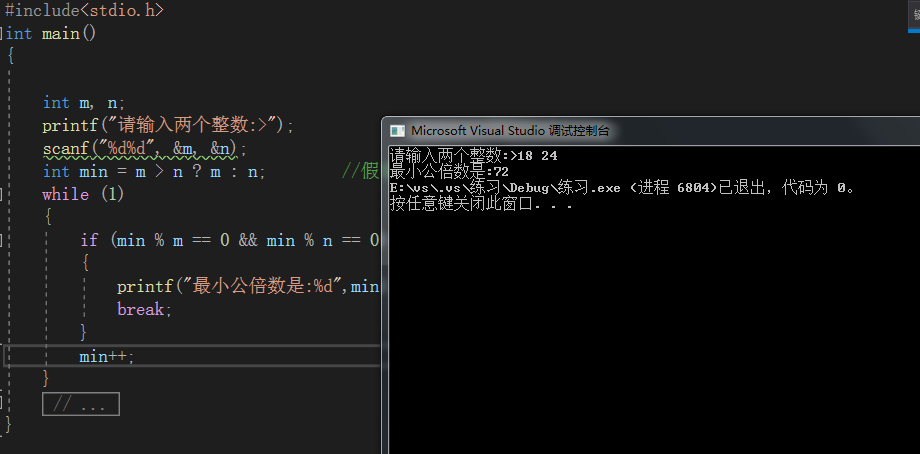

• 法二
  这里给一个数学的公式:最小公倍数=两个数之和/最大公约数.这个方法只需要求出最大公约数和两数之和相除即可.
  代码如下:

#include<stdio.h>
int main()
{
    
	int m, n;
	printf("请输入两个整数:>");
	scanf("%d%d", &m, &n);
	int max = m < n ? m : n;		//假设最大公约数
	while (1)
	{
    
		if (m % max == 0 && n % max == 0)
		{
    
			printf("最大公约数是:%d\n", max);
			break;
		}
		max--;
	}
	printf("最小公倍数是:%d", m * n / max);
}

测试结果: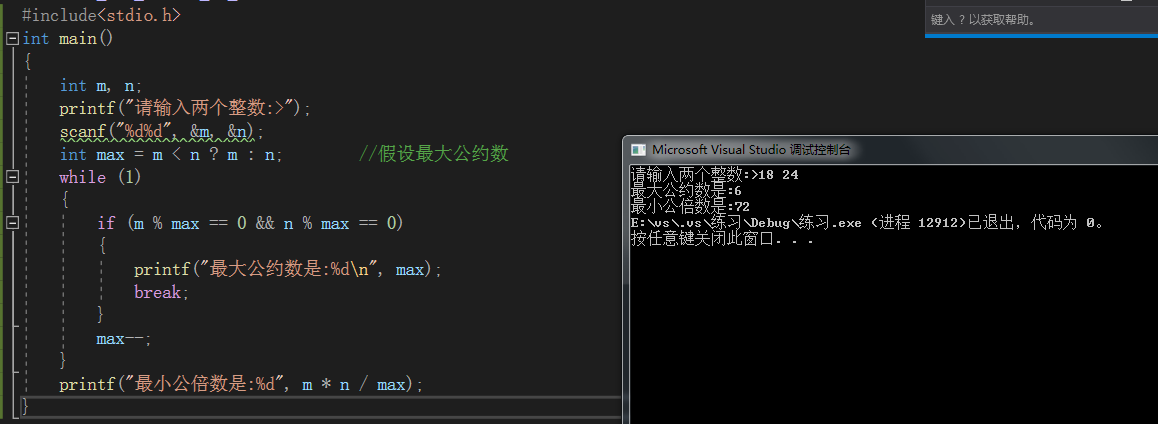

结言

这两道小菜还合口吧！我知道有的高手不过瘾，后续我们会越来越难的。前期要先热热身，希望你们有收获！我们下节见！