连续时间系统的性能分析（2）-二阶系统性能改善方式PID,PR

自控原理学习笔记
自控原理学习笔记专栏

---

---

4. 二阶系统性能改善

4.1 P-Proportion

4.1.1 开环传递函数：

$$L(s)=\frac{K_p{w}_n^2}{s(s+2\zeta w_n)}$$

4.1.2 系统闭环传递函数：

$$\Phi (s)=\frac{Y(s)}{R(s)}=\frac{K_p{w}_n^2}{s^2+2\zeta w_{n}s+K_p{w}_n^2}=\frac{w_{np}^2}{s^2+2{\zeta }_p{w}_{np}s+w_{np}^2}$$

4.1.3对比典型环节

1. 特征根的实部未变化

2. 闭环增益$\Phi (s){|}_{s=0}=1$不变化；开环速度增益$K=s^{1}L(s){|}_{s=0}=\frac{K_p{w}_n}{2\zeta }$

3. 固有频率$w_{np}=\sqrt{K_p}{w}_n$

4. 阻尼系数${\zeta }_p=\zeta /\sqrt{K_p}$

5. 调节时间基本不变

4.2 PD-Proportion Derivate

4.2.1开环传递函数

$$L(s)=\frac{(T_{d}s+1)w_n^2}{s\left(s+2\zeta w_n\right)}$$

4.2.2闭环传递函数

$$\Phi (s)=\frac{Y(s)}{R(s)}=\frac{w_n^2(T_{d}s+1)}{s^2+2\zeta w_{n}s+w_n^2{T}_{d}s+w_n^2}=\frac{w_n^2(T_{d}s+1)}{s^2+2{\zeta }_d{w}_{n}s+w_n^2}$$

4.2.3对比典型环节

1. 闭环增益为1，开环增益为$K=\frac{w_n}{2\zeta }$

2. 自然频率没有变换，阻尼系数变大，超调量变小——${\zeta }_d=\zeta +\frac{T_d{w}_n}{2}$

3. 系统阶跃响应等价于增加了一项冲激响应，幅度为$T_d$倍，加快系统动态响应
   $$Y(s)=\frac{w_n^2}{s^2+2{\zeta }_d{w}_{n}s+w_n^2}\ast \frac{1}{s}+\frac{w_n^2\cdot T_d}{s^2+2{\zeta }_d{w}_{n}s+w_n^2}$$

4.2.4 定性结论

1. 增加系统阻尼比，不影响系统的自然频率，从而抑制振荡，使超调减弱，改善系统平稳性。
2. 零点出现，加快系统的响应速度
3. 微分对高频噪声具有放大作用，输入噪声较大时，不宜使用

4.3 PI-Proportion Integral

4.3.1 开环传递函数

$$L(s)=\frac{(T_{i}s+1)w_n^2}{T_i{s}^2\left(s+2\zeta w_n\right)}$$

4.3.2 闭环传递函数

$$\begin{gathered} \frac{Y(s)}{R(s)}=\frac{{\omega }_{\mathrm{n}}^2\left(T_{\mathrm{i}}s+1\right)}{T_{\mathrm{i}}{s}^3+2T_{\mathrm{i}}\zeta {\omega }_{\mathrm{n}}{s}^2+T_{\mathrm{i}}{\omega }_{\mathrm{n}}{}^{2}s+{\omega }_{\mathrm{n}}^2} \\ \frac{Y(s)}{D(s)}=\frac{{\omega }_{\mathrm{n}}^2{T}_{\mathrm{i}}s}{T_{\mathrm{i}}{s}^3+2T_{\mathrm{i}}\zeta {\omega }_{\mathrm{n}}{s}^2+T_{\mathrm{i}}{\omega }_{\mathrm{n}}{}^{2}s+{\omega }_{\mathrm{n}}^2} \end{gathered}$$

4.3.3对比典型环节

1. 给定到输出闭环位置增益为1
2. 开环加速度增益为$K=s^{2}L(s){|}_{s=0}=\frac{w_n}{2\zeta T_i}$
3. 扰动到输出传递函数静态增益为0
4. 系统阶次由1阶变为2阶

4.3.4 定性结论

1. 系统阶次上升，不恰当选择参数可能造成产生RHP极点
2. 引入积分环节，消除恒值扰动引起的误差
3. 积分环节降低响应速度，响应初期可能增加超调量

4.4 PID-Proportion Integral Derivate

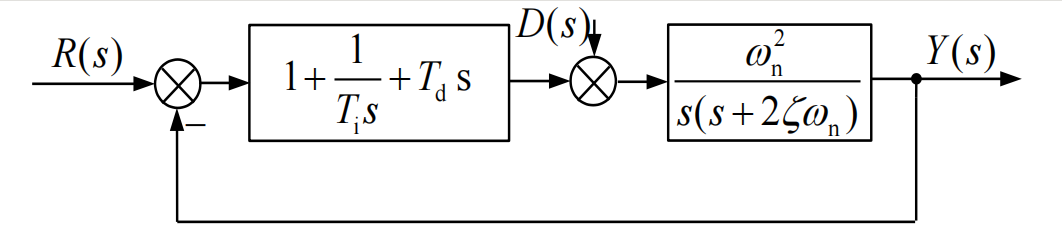
4.4.1 开环传递函数

$$L(s)=\frac{(T_i{T}_d{s}^2+T_{i}s1)w_n^2}{T_i{s}^2\left(s+2\zeta w_n\right)}$$

4.4.2闭环传递函数

$$\begin{gathered} \frac{Y(s)}{R(s)}=\frac{T_{\mathrm{d}}{T}_{\mathrm{i}}{\omega }_{\mathrm{n}}^2{s}^2+T_{\mathrm{i}}{\omega }_{\mathrm{n}}^{2}s+{\omega }_{\mathrm{n}}^2}{T_{\mathrm{i}}{s}^3+\left(2T_{\mathrm{i}}\zeta {\omega }_{\mathrm{n}}+T_{\mathrm{d}}{T}_{\mathrm{i}}{\omega }_{\mathrm{n}}^2\right)s^2+T_{\mathrm{i}}{\omega }_{\mathrm{n}}^{2}s+{\omega }_{\mathrm{n}}^2} \\ \frac{Y(s)}{D(s)}=\frac{{\omega }_{\mathrm{n}}^2{T}_{\mathrm{i}}s}{T_{\mathrm{i}}{s}^3+\left(2T_{\mathrm{i}}\zeta {\omega }_{\mathrm{n}}+T_{\mathrm{d}}{T}_{\mathrm{i}}{\omega }_{\mathrm{n}}^2\right)s^2+T_{\mathrm{i}}{\omega }_{\mathrm{n}}^{2}s+{\omega }_{\mathrm{n}}^2} \end{gathered}$$

4.4.3 对比典型环节

1. 给定到输出闭环位置增益为1
2. 开环加速度增益为$K=s^{2}L(s){|}_{s=0}=\frac{w_n}{2\zeta T_i}$
3. 扰动到输出传递函数静态增益为0
4. 系统阶次由1阶变为2阶

4.4.4定性结论

1. P——提升响应速度；I——消除稳态误差；D——适当加快暂态响应，压制超调量
2. 消除恒值扰动引起误差。

4.5微分反馈

4.5.1 开环传递函数：

$$L(s)=\frac{{\omega }_{\mathrm{n}}^2}{s\left(2\zeta {\omega }_{\mathrm{n}}+k{\omega }_{\mathrm{n}}{}^2\right)}$$

4.5.2 闭环传递函数：

$$\frac{Y(s)}{R(s)}=\frac{{\omega }_{\mathrm{n}}^2}{s^2+\left(2\zeta {\omega }_{\mathrm{n}}+k{\omega }_{\mathrm{n}}{}^2\right)s+{\omega }_{\mathrm{n}}^2}$$

4.5.3 对比典型环节

1. 闭环位置增益为1
2. 开环速度增益减小为$K=\frac{w_n^2}{2\zeta w_n+k{w}_n^2}$
3. 自然频率未变
4. 阻尼系数变大${\zeta }_{df}=\zeta +\frac{1}{2}k{w}_n$

4.4.5定性结论

1. 不影响自然频率，使系统阻尼比增加，减小超调量
2. 降低开环增益，加大系统斜坡输入稳态误差
3. 不形成闭环零点，输出平稳性优于PD调节