当前位置:网站首页>[special topic] summary of RMQ question brushing with ST table
[special topic] summary of RMQ question brushing with ST table
2022-07-27 11:31:00 【There are fish in Beiming - its name is salty】
【 project 】 use ST Table resolution RMQ Sum up the questions
It's a long time since I last wrote a blog ( I'm really an old lazy dog )
Come to the point , Put the topic links and codes directly
kuangbin rmq project
This contest There are ten questions in it, but there are actually 2 Avenue dp The question of is mixed into it , There's another water problem that doesn't need rmq Can do ( However, if you are in charge, you can force rmq), There's another one HYSBZ The question above Because of laziness Didn't do ... Then it's left 6 It's a question , Press the difficulty and type one by one ( A one-dimensional rmq/ A two-dimensional rmq) Pendulum code
A one-dimensional rmq(4 Avenue ):
POJ3264
On the meaning of the title ... Namely rmq Board question , If you have a hand
//POJ3264
#include <iostream>
#include <cstdio>
#include <cmath>
using namespace std;
const int maxn=5e4+5;
int mx[maxn][17],mi[maxn][17];
int a[maxn],n,q;
void rmqinit(){
for(int i=1;i<=n;i++) mx[i][0]=mi[i][0]=a[i];
for(int j=1;j<=16;j++)
for(int i=1;i+(1<<j)-1<=n;i++)
mx[i][j]=max(mx[i][j-1],mx[i+(1<<(j-1))][j-1]),
mi[i][j]=min(mi[i][j-1],mi[i+(1<<(j-1))][j-1]);
}
int rmq(int l,int r){
int d=log2(r-l+1);
int maxx=max(mx[l][d],mx[r-(1<<d)+1][d]);
int minn=min(mi[l][d],mi[r-(1<<d)+1][d]);
return maxx-minn;
}
int main()
{
scanf("%d%d",&n,&q);
for(int i=1;i<=n;i++) scanf("%d",&a[i]);
rmqinit();
while(q--){
int l,r;
scanf("%d%d",&l,&r);
printf("%d\n",rmq(l,r));
}
}
POJ3368
The question : I'll give you a sequence , Yes n Number a1,a2,….,an, And it is not reduced , Satisfy ai <= ai+1(1<=i<n). existing m Time to ask , The result of each inquiry is [l,r] How many times does the number with the most times appear in the interval .
Ideas : The maintenance interval of anencephalic segment tree is the maximum and the number of left and right values and the occurrence of left and right values ( Since it is rmq project , Certainly rmq 了 ) Because the sequence of numbers is not reduced, the same values are together , Using arrays b[i] Record the current value a[i] Is the same value of the first few occurrences , Then you can rmq The maximum number of queries appears , However, there is a problem if the value found is the left end of the query interval , Part of the front is no longer in the interval , So open another c[] Array , Sweep backwards , Record the current and each a[i] What is the right boundary of a continuous sequence of the same value , When querying, it is directly divided into the left end l To c[l], Again from c[l]+1 To r Conduct rmq The last two is max that will do
//POJ3368
#include <iostream>
#include <cstdio>
#include <cstring>
#include <cmath>
using namespace std;
const int maxn=1e5+5;
int f[maxn][18],a[maxn],b[maxn],c[maxn],n,q;
void rmqinit(){
for(int i=1;i<=n;i++) f[i][0]=b[i];
for(int j=1;j<=17;j++)
for(int i=1;i+(1<<j)-1<=n;i++)
f[i][j]=max(f[i][j-1],f[i+(1<<(j-1))][j-1]);
}
int rmq(int l,int r){
if(l>r) return 0;
int d=log2(r-l+1);
return max(f[l][d],f[r-(1<<d)+1][d]);
}
int main()
{
while(~scanf("%d",&n)&&n){
scanf("%d",&q);
for(int i=1;i<=n;i++) scanf("%d",&a[i]);
for(int i=1;i<=n;i++){
if(i==1||a[i]!=a[i-1]) b[i]=1;
else b[i]=b[i-1]+1;
}
int rbound=n;
for(int i=n;i>0;i--){
if(i==n||b[i]==b[i+1]-1) c[i]=rbound;
else c[i]=rbound=i;
}
rmqinit();
while(q--){
int l,r;
scanf("%d%d",&l,&r);
int ans1=min(c[l],r)-l+1;
int ans2=rmq(min(c[l],r)+1,r);
printf("%d\n",max(ans1,ans2));
}
}
}
HDU3183
The question : Give a string of numbers with a length of n, Let you delete m Number , Make the remaining number smallest after removing the leading zero
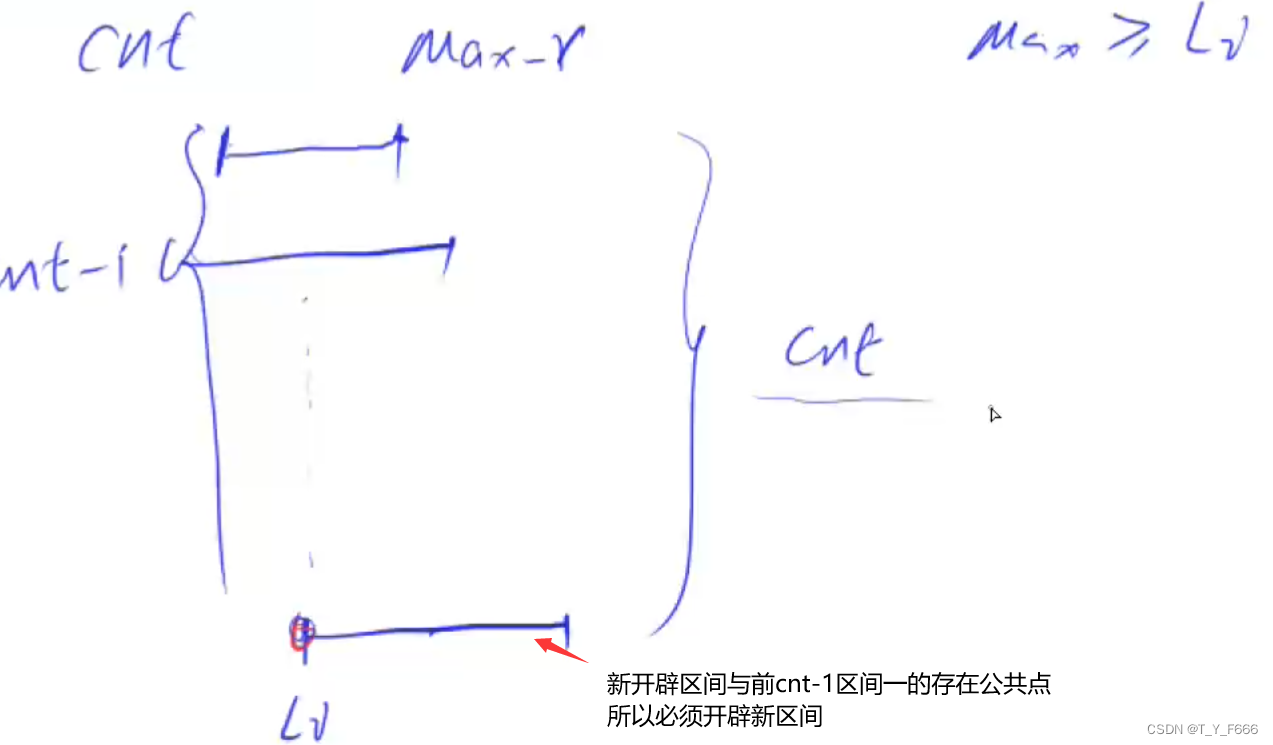
Ideas : Of course, I think of mindless greed , Consider deleting only one number , The best is to sweep from front to back , When encountering a pair of adjacent decreasing numbers , Just delete the big one in front , The data range of this problem is that violence is also passable , however !rmq How to do it? ??? Only after reading other people's ideas can I understand , The answer is n-m digit ( Keep leading zeros ), First rmq look for 1 To (m+1) The smallest number in it ( The first id individual ), This number must be the first answer , And then find id+1 To m+2 The smallest , This is the second answer .... And so on .
by the way rmq Maintain the subscript of the interval minimum , It's not worth it , I don't want to use the trinocular operator , So it's overloaded min function ...
Pit point : If you delete them all, you should output them finally 0, Not empty ,wa For a long time ...
//HDU3183
#include <iostream>
#include <cstdio>
#include <cstring>
#include <cmath>
using namespace std;
const int maxn=1e3+5;
char ch[maxn];
int m,n,f[maxn][11],ans[maxn];
inline int min(int x,int y){
if(ch[x]==ch[y]) return x<y?x:y;
return ch[x]<ch[y]?x:y;
}
void rmqinit(){
for(int i=1;i<=n;i++) f[i][0]=i;
for(int j=1;j<=10;j++)
for(int i=1;i+(1<<j)-1<=n;i++)
f[i][j]=min(f[i][j-1],f[i+(1<<(j-1))][j-1]);
}
int rmq(int l,int r){
int d=log2(r-l+1);
return min(f[l][d],f[r-(1<<d)+1][d]);
}
int main()
{
while(~scanf("%s%d",ch+1,&m)){
n=strlen(ch+1);
rmqinit();
int l=0,r=m+1,cnt=0;
while(r<=n){
l=rmq(l+1,r);
r++;
ans[++cnt]=l;
}
if(m==n){
puts("0");continue;}
int st=1;
while(ch[ans[st]]=='0'&&st<cnt) st++;
for(int i=st;i<=cnt;i++) printf("%c",ch[ans[i]]);
puts("");
}
}
HDU3486
The question : to n Number , Find the minimum number of segments , Make the sum of the maximum values of each segment greater than the given k. The length of each segment is equal , The last few are discarded .
Ideas : This problem requires a minimum number of intervals so that the sum of the maximum values of all intervals is greater than k, First preprocess the maximum value of each interval , Then enumerate the number of intervals ( Dichotomy is theoretically wrong , But it can AC,emmm), Calculate whether the sum is greater than k, The smallest interval number is the answer
//HDU3486
#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <cmath>
using namespace std;
const int maxn=2e5+5;
int n,k,a[maxn],f[maxn][19];
void rmqinit(){
for(int i=1;i<=n;i++) f[i][0]=a[i];
for(int j=1;j<=18;j++)
for(int i=1;i+(1<<j)-1<=n;i++)
f[i][j]=max(f[i][j-1],f[i+(1<<(j-1))][j-1]);
}
int rmq(int l,int r){
int d=log2(r-l+1);
return max(f[l][d],f[r-(1<<d)+1][d]);
}
int main()
{
while(~scanf("%d%d",&n,&k)){
if(n<0&&k<0) break;
int sum=0,maxx=0;
for(int i=1;i<=n;i++){
scanf("%d",&a[i]);
sum+=a[i],maxx=max(maxx,a[i]);
}
if(sum<=k){
puts("-1");
continue;
}
rmqinit();
int i;
for(i=max(1,(k+1)/maxx);i<=n;i++){
int len=n/i;
int tot=0;
for(int j=1;j<=i;j++){
tot+=rmq((j-1)*len+1,j*len);
if(tot>k) break;
}
if(tot>k) break;
}
printf("%d\n",i);
}
}
A two-dimensional rmq(2 Avenue ):
In fact, two-dimensional rmq And one dimension rmq My thoughts are almost , It is used to solve the two-dimensional interval maximum problem , There are two different implementation methods
Law 1 :1) O(nmlog(m)) Preprocessing ----O(n) Inquire about , Treat every line as one dimension RMQ Handle
Law two :2) O(nmlog(n)*log(m) Preprocessing ----O(1) Inquire about ,f[ i ][ j ][ k ][ l ] It means from the first point, that is, the upper left corner (i,j) rise , To the lower right corner (i+2^k, j+2^l) But it does not include the lower right corner and the right column and the down row , Then the large rectangle is divided into four small rectangles during preprocessing and query .
【 Be careful 】 In addition to one-dimensional rmq Handle it the same way f[i][j][0][0], At the same time, don't forget to deal with it in the same way as one dimension f[i][j][0][x] and f[i][j][x][0] The circumstances of .
POJ2019
The question : There's nothing to say , It's a board question , But the inquiry interval is square and the side length is fixed b, Query the maximum and minimum difference for the upper left corner coordinates
//POJ2019
#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <cmath>
using namespace std;
const int maxn=255;
int n,b,k;
int mx[maxn][maxn][9][9],mi[maxn][maxn][9][9];
int a[maxn][maxn];
void rmqinit(){
for(int i=1;i<=n;i++)
for(int j=1;j<=n;j++)
mx[i][j][0][0]=mi[i][j][0][0]=a[i][j];
for(int j=1;j<=n;j++)
for(int k1=1;k1<=8;k1++)
for(int i=1;i+(1<<k1)-1<=n;i++)
mx[i][j][k1][0]=max(mx[i][j][k1-1][0],mx[i+(1<<(k1-1))][j][k1-1][0]),
mi[i][j][k1][0]=min(mi[i][j][k1-1][0],mi[i+(1<<(k1-1))][j][k1-1][0]);
for(int i=1;i<=n;i++)
for(int k2=1;k2<=8;k2++)
for(int j=1;j+(1<<k2)-1<=n;j++)
mx[i][j][0][k2]=max(mx[i][j][0][k2-1],mx[i][j+(1<<(k2-1))][0][k2-1]),
mi[i][j][0][k2]=min(mi[i][j][0][k2-1],mi[i][j+(1<<(k2-1))][0][k2-1]);
for(int k1=1;k1<=8;k1++)
for(int k2=1;k2<=8;k2++)
for(int i=1;i+(1<<k1)-1<=n;i++)
for(int j=1;j+(1<<k2)-1<=n;j++)
mx[i][j][k1][k2]=max(max(mx[i][j][k1-1][k2-1],mx[i+(1<<(k1-1))][j][k1-1][k2-1]),max(mx[i][j+(1<<(k2-1))][k1-1][k2-1],mx[i+(1<<(k1-1))][j+(1<<(k2-1))][k1-1][k2-1])),
mi[i][j][k1][k2]=min(min(mi[i][j][k1-1][k2-1],mi[i+(1<<(k1-1))][j][k1-1][k2-1]),min(mi[i][j+(1<<(k2-1))][k1-1][k2-1],mi[i+(1<<(k1-1))][j+(1<<(k2-1))][k1-1][k2-1]));
}
int rmq(int x1,int y1,int x2,int y2){
int d1=log2(x2-x1+1);
int d2=log2(y2-y1+1);
int maxx=max(max(mx[x1][y1][d1][d2],mx[x2-(1<<d1)+1][y1][d1][d2]),max(mx[x1][y2-(1<<d2)+1][d1][d2],mx[x2-(1<<d1)+1][y2-(1<<d2)+1][d1][d2]));
int minn=min(min(mi[x1][y1][d1][d2],mi[x2-(1<<d1)+1][y1][d1][d2]),min(mi[x1][y2-(1<<d2)+1][d1][d2],mi[x2-(1<<d1)+1][y2-(1<<d2)+1][d1][d2]));
return maxx-minn;
}
int main()
{
scanf("%d%d%d",&n,&b,&k);
for(int i=1;i<=n;i++)
for(int j=1;j<=n;j++)
scanf("%d",&a[i][j]);
rmqinit();
while(k--){
int r,c;
scanf("%d%d",&r,&c);
printf("%d\n",rmq(r,c,r+b-1,c+b-1));
}
}
HDU2888
The question : Given a n * m Matrix , Re given q A asked , Every time I ask (r1,c1) It's the upper left corner ,(r2,c2) Is the maximum value of the sub rectangle in the lower right corner , And judge whether the maximum value appears in the 4 On the top corner
Ideas : It is also a board problem ...
//HDU2888
#include <iostream>
#include <cstdio>
#include <cmath>
#include <algorithm>
#include <cstring>
using namespace std;
const int maxn=305;
int m,n,q;
int mx[maxn][maxn][9][9];
void rmqinit(){
for(int i=1;i<=n;i++)
for(int j=1;j<=m;j++)
scanf("%d",&mx[i][j][0][0]);
for(int j=1;j<=m;j++)
for(int k1=1;k1<=8;k1++)
for(int i=1;i+(1<<k1)-1<=n;i++)
mx[i][j][k1][0]=max(mx[i][j][k1-1][0],mx[i+(1<<(k1-1))][j][k1-1][0]);
for(int i=1;i<=n;i++)
for(int k2=1;k2<=8;k2++)
for(int j=1;j+(1<<k2)-1<=m;j++)
mx[i][j][0][k2]=max(mx[i][j][0][k2-1],mx[i][j+(1<<(k2-1))][0][k2-1]);
for(int k1=1;k1<=8;k1++)
for(int k2=1;k2<=8;k2++)
for(int i=1;i+(1<<k1)-1<=n;i++)
for(int j=1;j+(1<<k2)-1<=m;j++)
mx[i][j][k1][k2]=max(max(mx[i][j][k1-1][k2-1],mx[i+(1<<(k1-1))][j][k1-1][k2-1]),max(mx[i][j+(1<<(k2-1))][k1-1][k2-1],mx[i+(1<<(k1-1))][j+(1<<(k2-1))][k1-1][k2-1]));
}
int rmq(int x1,int y1,int x2,int y2){
int d1=log2(x2-x1+1);
int d2=log2(y2-y1+1);
return max(max(mx[x1][y1][d1][d2],mx[x2-(1<<d1)+1][y1][d1][d2]),max(mx[x1][y2-(1<<d2)+1][d1][d2],mx[x2-(1<<d1)+1][y2-(1<<d2)+1][d1][d2]));
}
int main()
{
while(~scanf("%d%d",&n,&m)){
rmqinit();
for(scanf("%d",&q);q;q--){
int r1,c1,r2,c2;
scanf("%d%d%d%d",&r1,&c1,&r2,&c2);
int maxx=rmq(r1,c1,r2,c2);
printf("%d ",maxx);
if(mx[r1][c1][0][0]==maxx||mx[r1][c2][0][0]==maxx||mx[r2][c1][0][0]==maxx||mx[r2][c2][0][0]==maxx) puts("yes");
else puts("no");
}
}
}
边栏推荐
- C programming language (2nd Edition) -- Reading Notes -- 1.5.3
- 栈 AcWing 3302. 表达式求值
- Caused by:org.gradle.api.internal. plugins . PluginApplicationException: Failed to apply plugin
- ACM warm-up Exercise 1 in 2022 summer vacation (summary)
- Longest ascending subsequence model acwing 1014. mountaineering
- 第13章 IO流
- ACM warm-up Exercise 2 in 2022 summer vacation (summary)
- Knapsack problem acwing 9. grouping knapsack problem
- properties文件
- Longest ascending subsequence model acwing 1012. Sister Cities
猜你喜欢
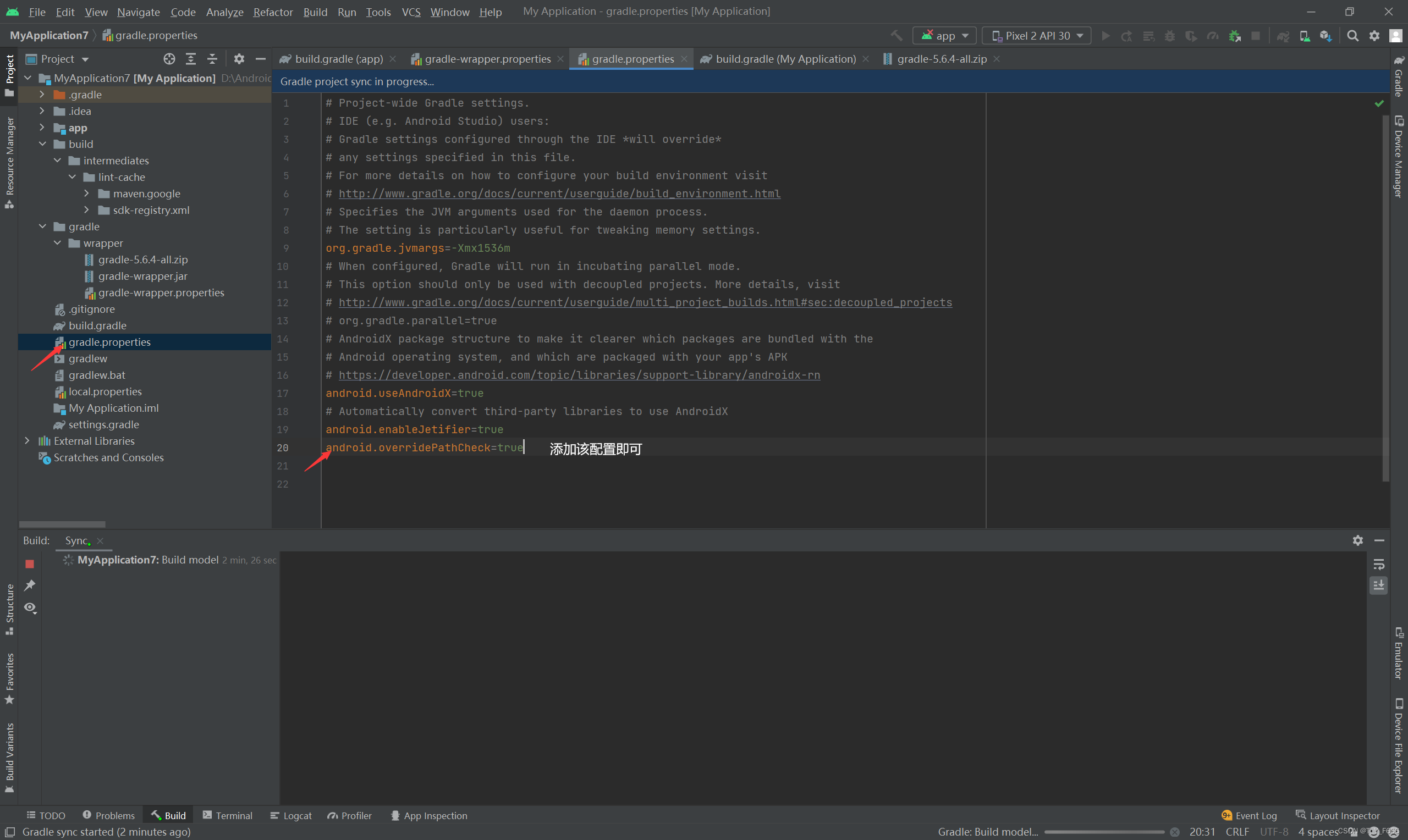
Caused by:org.gradle.api.internal. plugins . PluginApplicationException: Failed to apply plugin
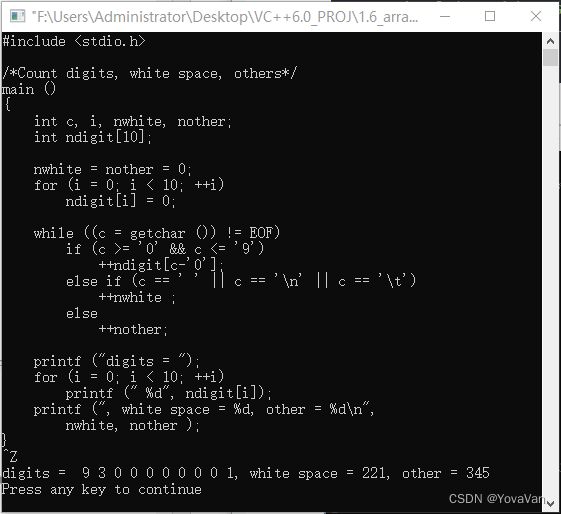
The C programming language (2nd) -- Notes -- 1.6

数字三角形模型 AcWing 1015. 摘花生

Inclusion exclusion principle acwing 890. divisible numbers

Tree DP acwing 285. dance without boss
Interval problem acwing 906. Interval grouping

第13章 IO流

WGet warning: unable to verify

背包模型 AcWing 423. 采药

Quantitative industry knowledge summary
随机推荐
Wechat push - template message parameter configuration
背包模型 AcWing 1024. 装箱问题
Budweiser, a well-known beer, plans to launch NFT in an attempt to unveil the "long planned" uplink?
C programming language (2nd Edition) -- Reading Notes -- 1.5
When std:: bind meets this
Maximized array sum after 13 K negations
最长上升子序列模型 AcWing 1014. 登山
容斥原理 AcWing 890. 能被整除的数
The longest ascending subsequence model acwing 1017. The glider wing of the strange thief Kidd
2022牛客多校 (3)J.Journey
区间问题 AcWing 906. 区间分组
求组合数 AcWing 889. 满足条件的01序列
C# 自定义集合
Redis simple to use
高斯消元 AcWing 883. 高斯消元解线性方程组
Luogu p1896 non aggression
Stm32f10x -- C Language-1
Smart pointer (shared_ptr, unique_ptr, weak_ptr)
背包问题 AcWing 9. 分组背包问题
Introduction to software vulnerability analysis (I)