（2022杭电多校五）C - Slipper （dijkstra+虚拟结点）

题目链接：杭电多校5 [Cloned] - Virtual Judge
题目：

样例输入：

1
6
6 1 2
3 5 2
2 4 6
5 2 2
5 6 20
3 8
6 5

样例输出：

12

题意：给定一棵根节点为1节点个数为n的树，每条边都有一个权值，假如u和v之间有一条权值为w的树，代表从u->v和从v->u的代价是w，接下来给定一个k和val，代表我可以选择花费val从第i层的任意一个节点跳至第i+k或者i-k的任意一个节点，前提是所要跳到的那一层是真实存在的，最后给我们一个起点和终点，问我们从起点到终点最小的代价是什么。

分析：这道题我一开始没想那么复杂，就直接把第i层的所有节点分别和第i-k层和i+k层所有节点连一条权值为val的双向边直接跑最短路即可，但是交了一发TLE了，算了一下复杂度才发现极端情况是O(n^2)的，肯定不行。

然后想到了一个思路就是说每一层建立一个虚拟节点，让该层所有节点与该虚拟节点连权值为0的双向边，然后每相差k层的两个虚拟节点之间建立一条权值为val的双向边再跑dijkstra，发现是wa了，造了一个样例才发现问题，就是说如果我在每一层建立一个虚拟节点并将其与本层所有节点之间连一条权值为0的双向边，那么我就等价于可以在同层之间进行随意传输，而且不耗费代价，因为假如u和v是同一层的两个节点，那么我先从u跳到本层虚拟节点，花费为0，再从本层虚拟节点跳至v，代价也是0，所以这样做显然是不行的。

我们需要避开上述的成环问题，最后对上述方案进行了更新，就是说我在每层建立两个虚拟节点l和r，那么我将本层所有节点都连一条到虚拟节点l但权值为0的单向边，然后再从虚拟节点r到本层各个节点连一条权值为0的单向边，而l和r之间无连边，这样同一层之内就不会出现上述的成环问题了，而实现k层之间的跳跃也很简单，比如要实现第i层和第i+k层的跳跃，那么我就让第i层的l节点连一条向第i+k层的r节点的权值为val的边，再从第i+k层的l节点连一条向第i层的r节点的权值为val的边，如图所示：

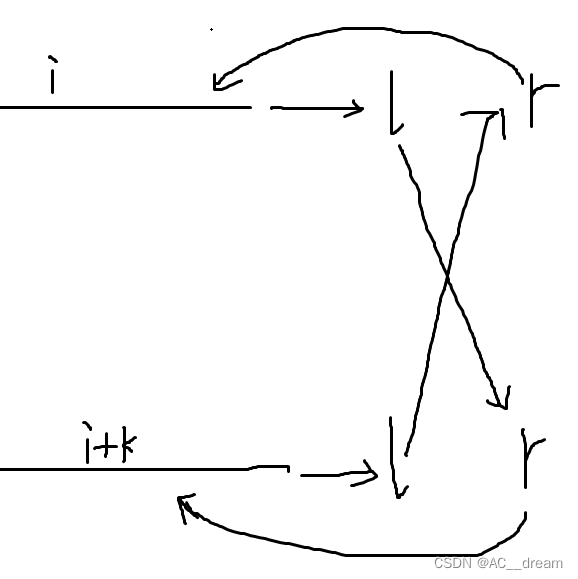
 最后直接从起点跑一个dijkstra即可。

下面是代码：

#include<cstdio>
#include<iostream>
#include<algorithm>
#include<cstring>
#include<map>
#include<queue>
#include<vector>
#include<cmath>
using namespace std;
const int N=1e6+10;
typedef pair<long long,int> PII;
int depth[N];
long long d[3*N];
int maxd,be,en,n;
vector<int>p[N];//p[i]记录高度为i的节点 
int h[N*3],e[N*10],ne[N*10],idx;
long long w[N*10];
bool vis[3*N];
void add(int x,int y,int z)
{
	e[idx]=y;
	w[idx]=z;
	ne[idx]=h[x];
	h[x]=idx++;
}
void dfs(int x,int fa)
{
	p[depth[x]].push_back(x);
	for(int i=h[x];i!=-1;i=ne[i])
	{
		int j=e[i];
		if(j==fa) continue;
		depth[j]=depth[x]+1;
		maxd=max(maxd,depth[j]);
		dfs(j,x);
	}
}
void dijkstra()
{
    for(int i=1;i<=3*n;i++)
    {
    	vis[i]=false;
    	d[i]=0x3f3f3f3f3f3f3f3f;
	}
    d[be]=0;
    priority_queue<PII,vector<PII>,greater<PII> >q;
    q.push({0,be});
    while(!q.empty())
    {
        int begin=q.top().second;
        q.pop();
        if(begin==en) return ;
        if(vis[begin]) continue;
        vis[begin]=true;
        for(int i=h[begin];i!=-1;i=ne[i])
        {
            int j=e[i];
            if(d[j]>d[begin]+w[i])
            {
                d[j]=d[begin]+w[i];
                q.push({d[j],j});
            }
        }
    }
}
int main()
{
	int T;
	cin>>T;
	while(T--)
	{
		scanf("%d",&n);
		idx=maxd=0;
		for(int i=1;i<=3*n;i++) h[i]=-1;
		for(int i=1;i<n;i++)
		{
			int u,v,w;
			scanf("%d%d%d",&u,&v,&w);
			add(u,v,w);add(v,u,w);
		}
		int k,val;
		scanf("%d%d",&k,&val);
		scanf("%d%d",&be,&en);
		depth[1]=1;
		dfs(1,-1);
		for(int i=1;i<=maxd;i++)
		for(int j=0;j<p[i].size();j++)
		{
			add(p[i][j],n+i,0);//建立虚拟节点l 
			add(2*n+i,p[i][j],0);//建立虚拟节点r 
		}
		for(int i=1;i+k<=maxd;i++)//虚拟节点之间连边 
		{
			add(n+i,2*n+k+i,val);
			add(n+k+i,2*n+i,val);
		}
		dijkstra();
		printf("%lld\n",d[en]);
		for(int i=1;i<=maxd;i++) p[i].clear();
	}
	return 0;
}