单调栈结构练习——子数组最小值的累加和

题目

给定一个数组arr，返回所有子数组最小值的累加和。

力扣链接：子数组的最小值之和

题解

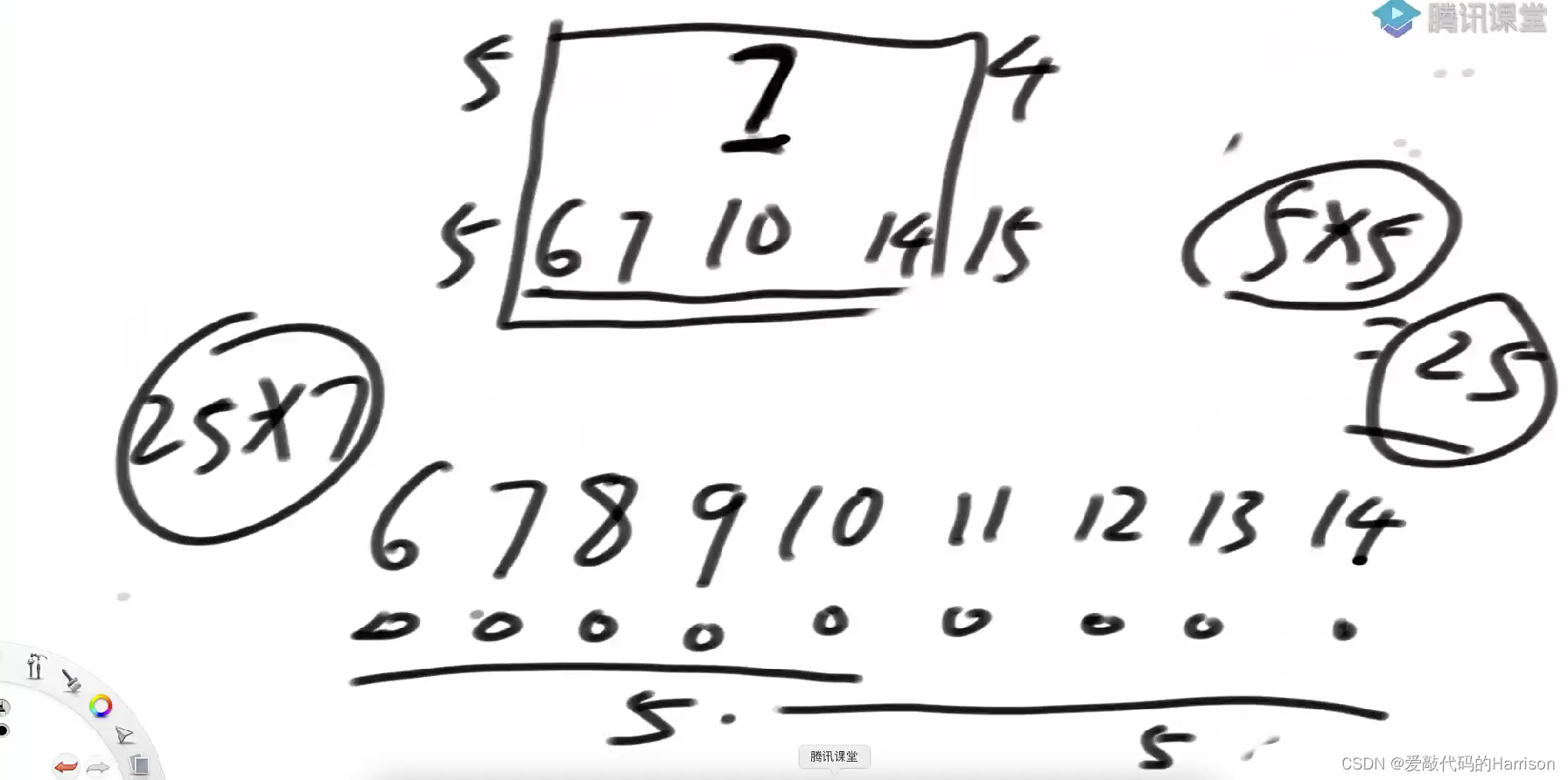
如上图，运用单调栈结构，左边比7小的且离它最近的位置是5，右边离它最近的且小于7的位置是15，所以以7为最小值的子数组分别有，6位置开头：6 ~ 10、6 ~ 11、6 ~ 12、6 ~ 13、6 ~ 14；7位置开头：7 ~ 10、7 ~ 11、7 ~ 12、7 ~ 13、7 ~ 14；8位置开头：8 ~ 10、8 ~ 11、8 ~ 12、8 ~ 13、8 ~ 14；9位置开头：9 ~ 10、9 ~ 11、9 ~ 12、9 ~ 13、9 ~ 14；10位置开头：10 ~ 10、10 ~ 11、10 ~ 12、10 ~ 13、10 ~ 14；所以整体子数组个数是25个（其实就是开头位置的个数 * 结尾位置的个数），每个子数组的最小值都是7，那么以7做最小值的所有子数组的累计和就是 25 * 7。

具体可以带入如下例子：

接下来推广一下，得到公式：( i - k ) * ( j - i ) * x（因为k位置和j位置都是到不了的！！！）

但是，以上讨论的都是认为数组没有重复值的情况！！！有重复值的话，讨论起来是挺复杂的！！！

如何计算以3位置上的3为最小值的所有子数组的数量？
1位置开头：1 ~ 3、1 ~ 4、1 ~ 5、1 ~ 6；
2位置开头：2 ~ 3、2 ~ 4、2 ~ 5、2 ~ 6；
3位置开头：3 ~ 3、3 ~ 4、3 ~ 5、3 ~ 6；

如何计算以7位置上的3为最小值的所有子数组的数量？
开头位置有变化！！！1 ~ 6位置整体属于开头位置。
1 ~ 7、1 ~ 8、1 ~ 9、1 ~ 10；
2 ~ 7、2 ~ 8、2 ~ 9、2 ~ 10；
…
7 ~ 7、7 ~ 8、7 ~ 9、7 ~ 10；

如何计算以11位置上的3为最小值的所有子数组的数量？
那么开头位置就是：1 ~ 10整体范围

计算以13位置上的3为最小值的所有子数组的数量也同理可得

package com.harrison.class14;

/** * @author Harrison * @create 2022-03-27-15:06 * @motto 众里寻他千百度，蓦然回首，那人却在灯火阑珊处。 */
public class Code06_SumOfSubarrayMinimums {
    
    public static int sumSubarrayMins1(int[] arr){
    
        int sum=0;
        for(int i=0; i<arr.length; i++){
    
            for(int j=i; j<arr.length; j++){
    
                int min=arr[i];
                for(int k=i+1; k<=j; k++){
    
                    min=Math.min(min,arr[k]);
                }
                sum+=min;
            }
        }
        return sum;
    }

    public static int sumSubarrayMins2(int[] arr){
    
        // left[i] = x : arr[i]左边，离arr[i]最近，<=arr[i]，位置在x
        int[] left=leftNearLessEqual2(arr);
        // right[i] = y : arr[i]右边，离arr[i]最近，< arr[i],的数，位置在y
        int[] right=rightNearLess2(arr);
        int ans=0;
        for(int i=0; i<arr.length; i++){
    
            int start=i-left[i];
            int end=right[i]-i;
            ans+=start*end*arr[i];
        }
        return ans;
    }

    public static int[] leftNearLessEqual2(int[] arr){
    
        int[] left=new int[arr.length];
        for(int i=0; i<arr.length; i++){
    
            int ans=-1;
            for(int j=i-1; j>=0; j--){
    
                if(arr[j]<=arr[i]){
    
                    ans=j;
                    break;
                }
            }
            left[i]=ans;
        }
        return left;
    }

    public static int[] rightNearLess2(int[] arr){
    
        int[] right=new int[arr.length];
        for(int i=0; i<arr.length; i++){
    
            int ans=arr.length;
            for(int j=i+1; j<arr.length; j++){
    
                if(arr[j]<arr[i]){
    
                    ans=j;
                    break;
                }
            }
            right[i]=ans;
        }
        return right;
    }

    public static int sumSubarrayMins3(int[] arr){
    
        int[] stack=new int[arr.length];
        // left[i]==x：arr[i]左边，离arr[i]最近，小于等于arr[i]的数的位置在x，如果没有x就是-1
        // right[i]==y，arr[i]右边，离arr[i]最近，小于arr[i]数的位置在y，如果没有y就是-1
        int[] left=leftNearLessEqual3(arr,stack);
        int[] right=rightNearLess3(arr,stack);
        long ans=0;
        for(int i=0; i<arr.length; i++){
    
            long start=i-left[i];// 左边到不了的位置算出一个开头数量
            long end=right[i]-i;// 右边到不了的位置算出一个结尾数量
            ans+=start*end*(long)arr[i];
            ans%=1000000007;
        }
        return (int)ans;
    }

    public static int[] leftNearLessEqual3(int[] arr,int[] stack){
    
        int N=arr.length;
        int[] left=new int[N];
        int size=0;
        for(int i=N-1; i>=0; i--){
    
            while(size!=0 && arr[i]<=arr[stack[size-1]]){
    
                left[stack[--size]]=i;
            }
            stack[size++]=i;
        }
        while(size!=0){
    
            left[stack[--size]]=-1;
        }
        return left;
    }

    public static int[] rightNearLess3(int[] arr,int[] stack){
    
        int N=arr.length;
        int[] right=new int[N];
        int size=0;
        for(int i=0; i<N; i++){
    
            while(size!=0 && arr[i]<arr[stack[size-1]]){
    
                right[stack[--size]]=i;
            }
            stack[size++]=i;
        }
        while(size!=0){
    
            right[stack[--size]]=N;
        }
        return right;
    }

    public static int[] randomArray(int len, int maxValue) {
    
        int[] ans = new int[len];
        for (int i = 0; i < len; i++) {
    
            ans[i] = (int) (Math.random() * maxValue) + 1;
        }
        return ans;
    }

    public static void printArray(int[] arr) {
    
        for (int i = 0; i < arr.length; i++) {
    
            System.out.print(arr[i] + " ");
        }
        System.out.println();
    }

    public static void main(String[] args) {
    
        int maxLen = 100;
        int maxValue = 50;
        int testTime = 100000;
        System.out.println("测试开始");
        for (int i = 0; i < testTime; i++) {
    
            int len = (int) (Math.random() * maxLen);
            int[] arr = randomArray(len, maxValue);
            int ans1 = sumSubarrayMins1(arr);
            int ans2 = sumSubarrayMins2(arr);
            int ans3 = sumSubarrayMins3(arr);
            if (ans1 != ans2 || ans1 != ans3) {
    
                printArray(arr);
                System.out.println(ans1);
                System.out.println(ans2);
                System.out.println(ans3);
                System.out.println("出错了！");
                break;
            }
        }
        System.out.println("测试结束");
    }
}