当前位置:网站首页>abc262-D(dp)
abc262-D(dp)
2022-08-05 10:28:00 【一条小小yu】
D - I Hate Non-integer Number Editorial

/
Time Limit: 2.5 sec / Memory Limit: 1024 MB
Score : 400400 points
Problem Statement
You are given a sequence of positive integers A=(a_1,\ldots,a_N)A=(a1,…,aN) of length NN.
There are (2^N-1)(2N−1) ways to choose one or more terms of AA. How many of them have an integer-valued average? Find the count modulo 998244353998244353.
Constraints
- 1 \leq N \leq 1001≤N≤100
- 1 \leq a_i \leq 10^91≤ai≤109
- All values in input are integers.
Input
Input is given from Standard Input in the following format:
NN a_1a1 \ldots… a_NaN
Output
Print the answer.
Sample Input 1 Copy
Copy
3 2 6 2
Sample Output 1 Copy
Copy
6
For each way to choose terms of AA, the average is obtained as follows:
If just a_1a1 is chosen, the average is \frac{a_1}{1}=\frac{2}{1} = 21a1=12=2, which is an integer.
If just a_2a2 is chosen, the average is \frac{a_2}{1}=\frac{6}{1} = 61a2=16=6, which is an integer.
If just a_3a3 is chosen, the average is \frac{a_3}{1}=\frac{2}{1} = 21a3=12=2, which is an integer.
If a_1a1 and a_2a2 are chosen, the average is \frac{a_1+a_2}{2}=\frac{2+6}{2} = 42a1+a2=22+6=4, which is an integer.
If a_1a1 and a_3a3 are chosen, the average is \frac{a_1+a_3}{2}=\frac{2+2}{2} = 22a1+a3=22+2=2, which is an integer.
If a_2a2 and a_3a3 are chosen, the average is \frac{a_2+a_3}{2}=\frac{6+2}{2} = 42a2+a3=26+2=4, which is an integer.
If a_1a1, a_2a2, and a_3a3 are chosen, the average is \frac{a_1+a_2+a_3}{3}=\frac{2+6+2}{3} = \frac{10}{3}3a1+a2+a3=32+6+2=310, which is not an integer.
Therefore, 66 ways satisfy the condition.
Sample Input 2 Copy
Copy
5 5 5 5 5 5
Sample Output 2 Copy
Copy
31
Regardless of the choice of one or more terms of AA, the average equals 55.
#include<bits/stdc++.h>
using namespace std;
const int MAXN =1e2 + 10;
const int MOD = 998244353;
long long a[MAXN],n,ans,dp[MAXN][MAXN][MAXN];
int main()
{
cin >> n;
for(int i = 1; i <= n; i++)
{
cin >> a[i];
}
for(int s = 1; s <= n; s++)
{
memset(dp,0,sizeof dp);
dp[0][0][0] = 1;
for(int i = 0; i < n; i++)
{
for(int j = 0; j <= s && j <= i; j++)
{
for(int k = 0; k < s; k++)
{
dp[i + 1][j][k] += dp[i][j][k];
dp[i + 1][j][k] %= MOD;
if(j != s)dp[i + 1][j + 1][(k + a[i + 1]) % s] += dp[i][j][k];
dp[i + 1][j + 1][(k + a[i + 1]) % s] %= MOD;
}
}
}
ans += dp[n][s][0];
ans %= MOD;
}
cout << ans;
}
边栏推荐
- [Translation] Chaos Net + SkyWalking: Better observability for chaos engineering
- The JVM collection that Alibaba's top architects have summarized for many years, where can't I check it!
- 阿里顶级架构师多年总结的JVM宝典,哪里不会查哪里!
- 第五章:redis持久化,包括rdb和aof两种方式[通俗易懂]
- 单片机:温度控制DS18B20
- 用KUSTO查询语句(KQL)在Azure Data Explorer Database上查询LOG实战
- R语言使用yardstick包的pr_curve函数评估多分类(Multiclass)模型的性能、查看模型在多分类每个分类上的ROC曲线(precision(精准率),R代表的是recall(召回率)
- 导火索:OAuth 2.0四种授权登录方式必读
- The fuse: OAuth 2.0 four authorized login methods must read
- 告白数字化转型时代:麦聪软件以最简单的方式让企业把数据用起来
猜你喜欢
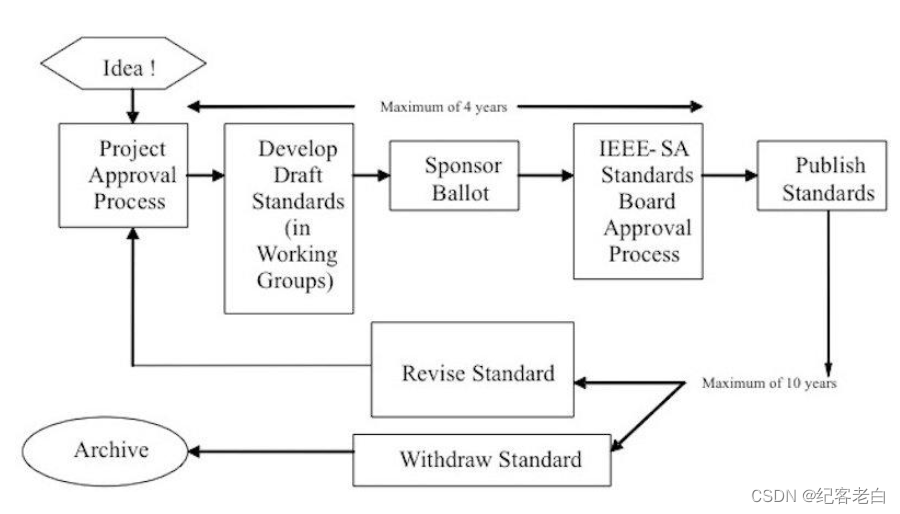
电气工程的标准是什么
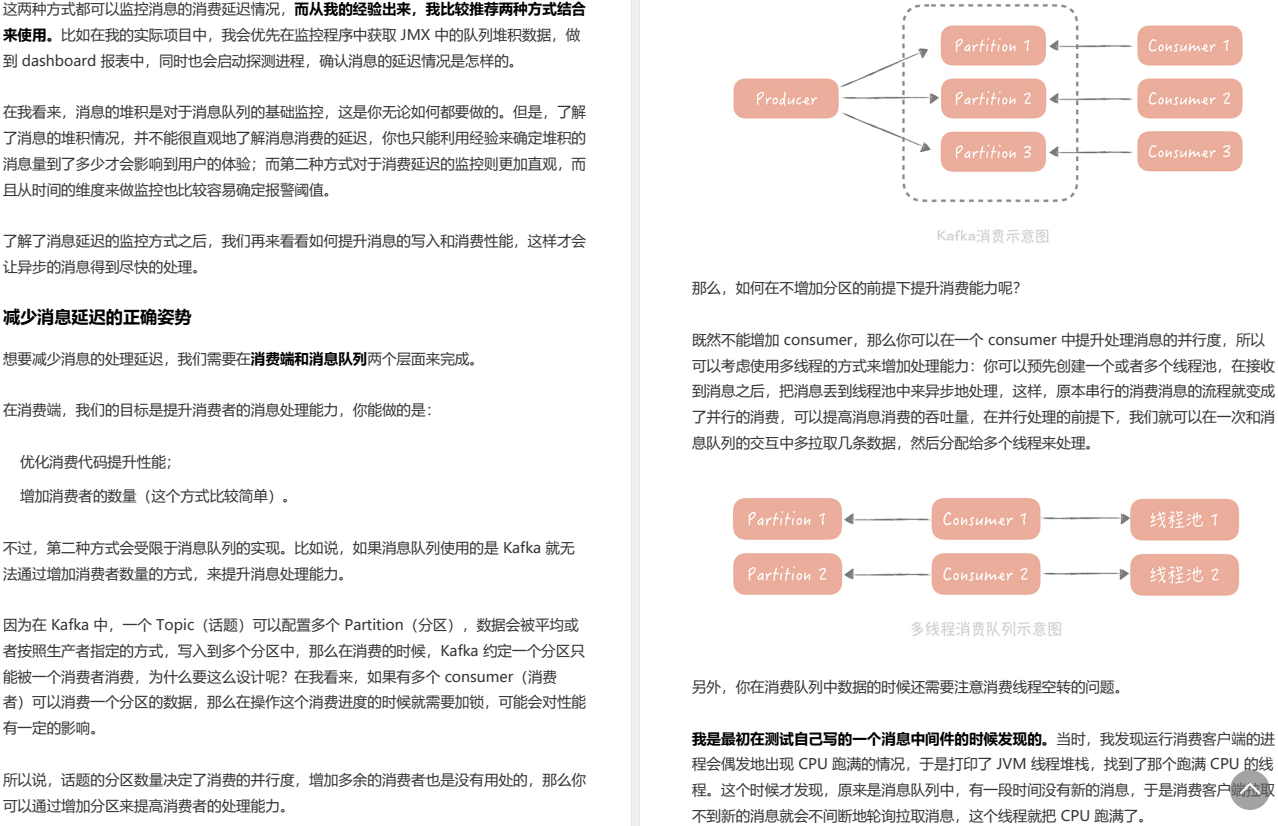
化繁为简!阿里新产亿级流量系统设计核心原理高级笔记(终极版)

What is SPL?
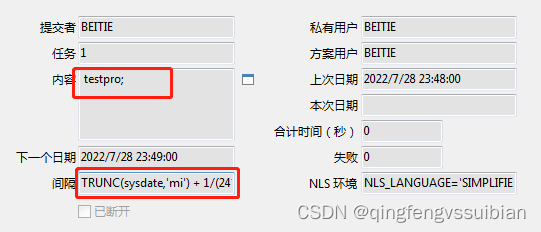
linux下oracle常见操作以及日常积累知识点(函数、定时任务)

three.js debugging tool dat.gui use

Confessing in the era of digital transformation: Mai Cong Software allows enterprises to use data in the easiest way
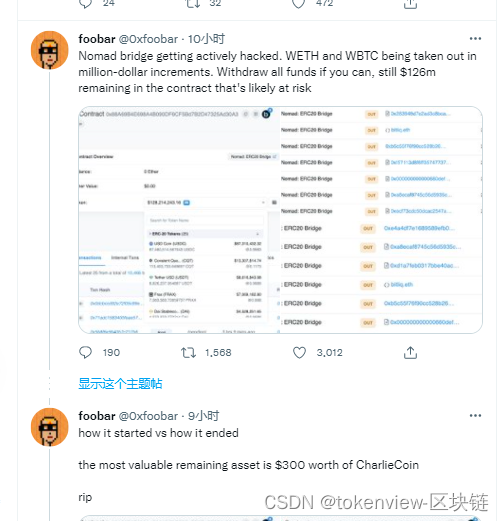
First Decentralized Heist?Loss of nearly 200 million US dollars: analysis of the attack on the cross-chain bridge Nomad
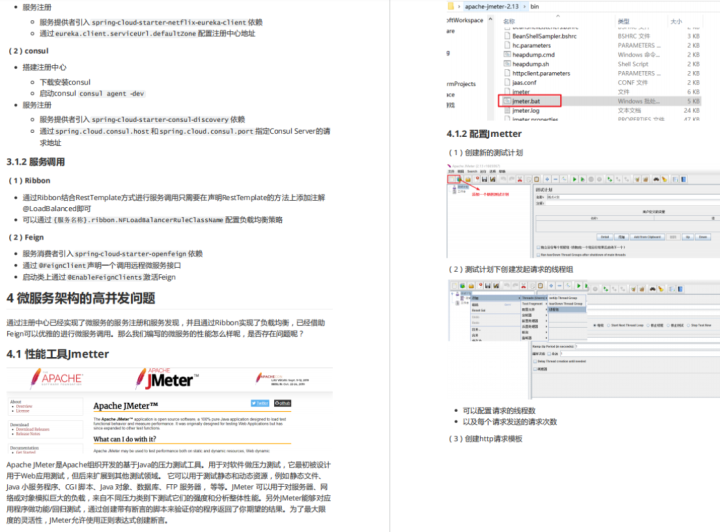
阿里全新推出:微服务突击手册,把所有操作都写出来了PDF
Still looking for a network backup resources?Hurry up to collect the following network backup resource search artifact it is worth collecting!
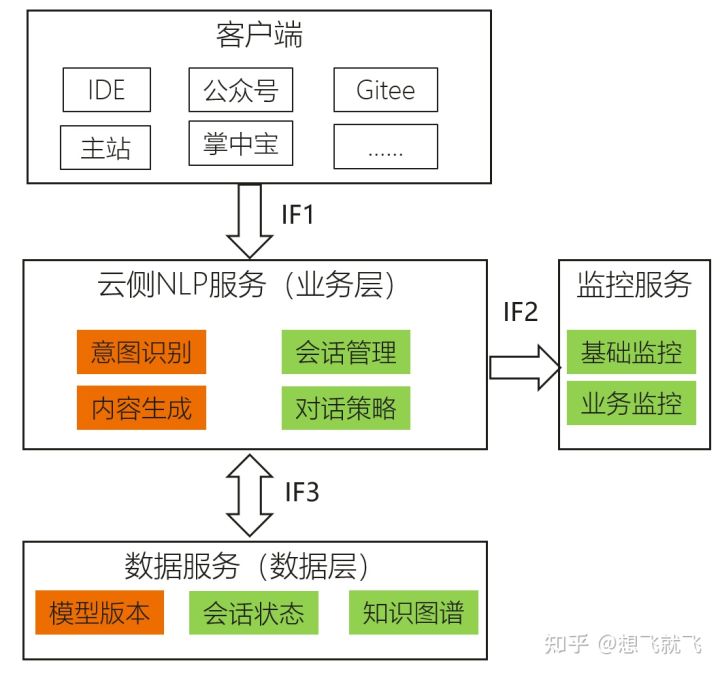
【MindSpore易点通机器人-01】你也许见过很多知识问答机器人,但这个有点不一样
随机推荐
012年通过修补_sss_提高扩散模型效率
nyoj86 找球号(一) set容器和二分 两种解法
What is SPL?
2022华数杯数学建模思路分析交流
华为轻量级神经网络架构GhostNet再升级,GPU上大显身手的G-GhostNet(IJCV22)
项目成本控制如何帮助项目成功?
一文道清什么是SPL
Meteorological data processing example - matlab string cutting matching and R language date matching (data splicing)
This notebook of concurrent programming knowledge points strongly recommended by Ali will be a breakthrough for you to get an offer from a big factory
数分面试(一)----与业务相关
Offensive World-PWN-new_easypwn
FPGA:基础入门LED灯闪烁
【MindSpore Easy-Diantong Robot-01】You may have seen many knowledge quiz robots, but this one is a bit different
Login function and logout function (St. Regis Takeaway)
2022 Huashu Cup Mathematical Modeling Question A Optimization Design Ideas for Ring Oscillators Code Sharing
气象数据数据处理实例——matlab字符串切割匹配与R语言日期匹配(数据拼接)
Technical dry goods | Hausdorff distance for image segmentation based on MindSpore
JS introduction to reverse the recycling business network of learning, simple encryption mobile phone number
基于MindSpore高效完成图像分割,实现Dice!
创建一个 Dapp,为什么要选择波卡?