当前位置:网站首页>2022杭电多校 第6场 1008.Shinobu Loves Segment Tree 规律题
2022杭电多校 第6场 1008.Shinobu Loves Segment Tree 规律题
2022-08-05 10:08:00 【HeartFireY】
题目分析
本题解时间复杂度 O ( T log n ) O(T\log n) O(Tlogn),标程 O ( T log 2 n ) O(T \log^2 n) O(Tlog2n)
发现每个节点的按顺序 b u i l d build build产生的加法序列的规律:(若干个 1 1 1)+(相同个数个 2 , 3 , 4... 2,3,4... 2,3,4...)+(若干个相同数字),然后发现加 2 , 3 , 4 , . . . 2,3,4,... 2,3,4,...的次数与层节点个数有关。即为加 2 ⌊ l o g 2 x ⌋ 2^{ {\lfloor log_2{x} \rfloor}} 2⌊log2x⌋次 2 , 3 , 4 , … 2,3,4,\dots 2,3,4,…。
这个规律可以通过 1. 1. 1.分析线段树 b u i l d build build性质 2. 2. 2.暴力打表(牛逼) 发现
那么我们可以写成式子:假设加法序列长度为 s i z siz siz,加 1 1 1的个数为 c n t 1 cnt_1 cnt1,那么该节点 r t rt rt的加和可以表示为:
c n t 1 + ( ( ( s i z − c n t 1 ) ( 2 ⌊ l o g 2 x ⌋ ) + 1 ) × ( ( s i z − c n t 1 ) ( 2 ⌊ l o g 2 x ⌋ ) + 2 ) 2 − 1 ) × 2 ⌊ l o g 2 x ⌋ + [ ( s i z − c n t 1 ) m o d ( 2 ⌊ l o g 2 x ⌋ ) ) ] × ( ( s i z − c n t 1 ) ( 2 ⌊ l o g 2 x ⌋ ) + 2 ) cnt_1 + (\frac{(\frac{(siz - cnt1)}{(2^{ {\lfloor log_2{x} \rfloor}})} + 1) \times (\frac{(siz - cnt1)}{(2^{ {\lfloor log_2{x} \rfloor}})} + 2)}{2} - 1) \times 2^{ {\lfloor log_2{x} \rfloor}} + [(siz - cnt_1) \mod (2^{ {\lfloor log_2{x} \rfloor}}))] \times (\frac{(siz - cnt1)}{(2^{ {\lfloor log_2{x} \rfloor}})} + 2) cnt1+(2((2⌊log2x⌋)(siz−cnt1)+1)×((2⌊log2x⌋)(siz−cnt1)+2)−1)×2⌊log2x⌋+[(siz−cnt1)mod(2⌊log2x⌋))]×((2⌊log2x⌋)(siz−cnt1)+2)加的数字个数 s i z siz siz的规律,对于当前节点 r t rt rt:
- ⌈ ( r t − 2 ⌊ l o g 2 r t ⌋ ) / 2 ⌉ m o d 2 = = 1 , s i z − = 2 ⌊ l o g 2 r t ⌋ − 2 \lceil(rt - 2^{\lfloor log_2{rt} \rfloor}) / 2 \rceil \mod2 == 1, siz -= 2^{\lfloor log_2{rt} \rfloor - 2} ⌈(rt−2⌊log2rt⌋)/2⌉mod2==1,siz−=2⌊log2rt⌋−2
- ⌈ ( r t − 2 ⌊ l o g 2 r t ⌋ ) / 2 ⌉ m o d 2 = = 0 , s i z − = 2 ⌊ l o g 2 r t ⌋ − 1 \lceil(rt - 2^{\lfloor log_2{rt} \rfloor}) / 2 \rceil \mod2 == 0, siz -= 2^{\lfloor log_2{rt} \rfloor - 1} ⌈(rt−2⌊log2rt⌋)/2⌉mod2==0,siz−=2⌊log2rt⌋−1
求 s i z siz siz时,可以令 s i z = n siz = n siz=n,然后沿着树上路径(实际上对应数字的二进制位)向上走,然后减去当前节点对应该减的值。
1 1 1的规律:可以 O ( 1 ) O(1) O(1)求:
c n t 1 = { 2 ( ⌊ l o g 2 x ⌋ − 1 ) , ( x − 2 ⌊ l o g 2 x ⌋ + 1 ) m o d 2 = 1 2 ⌊ l o g 2 x ⌋ , ( x − 2 ⌊ l o g 2 x ⌋ + 1 ) m o d 2 = 0 cnt_1 =\left\{\begin{matrix} 2^{({\lfloor log_2{x} \rfloor} - 1)},\ (x - 2^{ {\lfloor log_2{x} \rfloor}} + 1) \mod 2 =1 \\ 2^{ {\lfloor log_2{x} \rfloor}},\ (x - 2^{ {\lfloor log_2{x} \rfloor}} + 1) \mod 2 = 0 \end{matrix}\right. cnt1={ 2(⌊log2x⌋−1), (x−2⌊log2x⌋+1)mod2=12⌊log2x⌋, (x−2⌊log2x⌋+1)mod2=0注意,当 s i z < 0 siz < 0 siz<0时,特判输出 0 0 0,对第一层求 s i z siz siz时也要特判避免溢出。同时对 n = 1 n = 1 n=1的 4 4 4种情况也要特判,避免溢出。
Code
#include <bits/stdc++.h>
#pragma gcc optimize("O2")
#pragma g++ optimize("O2")
#define int long long
#define endl '\n'
using namespace std;
const int N = 2e5 + 10, MOD = 1e9 + 7;
inline void solve(){
int n = 0, x = 0; cin >> n >> x;
if(n == 1 && x == 1){
cout << 1 << endl; return; }
else if(n == 1 && x != 1){
cout << 0 << endl; return; }
if(x == 1){
cout << (n * (n + 1) / 2) << endl; return; }
//cout << "FUCK:" << get_range(x) << endl;
//if(x > get_range(x)){ cout << 0 << endl; return; }
int ceng = log2(x), ceng_fir = (1 << (ceng));
int cnt1 = ((x - ceng_fir + 1) % 2) ? (1 << (ceng - 1)) : ceng_fir;
if((x - ceng_fir + 1) == 0) cnt1 = ceng_fir;
// cnt_1 -> 1的个数
int siz = n;
int rt = x;
while(rt != 2 && rt != 3){
// cout << rt << " BEF | ";
int ceng_now = log2(rt) + 1, ser = rt - (1 << (ceng_now - 1)) + 1;
int md = ser % 4;
if(md == 1 || md == 2) siz -= (1 << (ceng_now - 3));
if(md == 3 || md == 0) siz -= (1 << (ceng_now - 2));
rt >>= 1;
// cout << rt << " AFT " << endl;
// cout << siz << endl;
}
if(rt != 1) siz -= 1;
if(siz <= 0){
cout << 0 << endl;
return;
}
if(siz <= cnt1){
cout << siz << endl;
return;
}
int yu = (siz - cnt1) % (ceng_fir), m = (siz - cnt1) / (ceng_fir);
int ans = yu * (m + 2) + cnt1 + ceng_fir * ((m + 1) * (m + 2) / 2 - 1);
cout << ans << endl;
}
signed main(){
ios_base::sync_with_stdio(false), cin.tie(0);
cout << fixed << setprecision(12);
int t = 1; cin >> t;
while(t--) solve();
return 0;
}
边栏推荐
- 第九章:activit内置用户组设计与组任务分配和IdentityService接口的使用
- Pycharm 常用外部工具
- Custom filters and interceptors implement ThreadLocal thread closure
- 韦东山 数码相框 项目学习(六)tslib的移植
- Four years of weight loss record
- Tanabata romantic date without overtime, RPA robot helps you get the job done
- 长达四年的减肥记录
- Handwriting Currying - toString Comprehension
- 第四章:redis 数组结构的set和一些通用命令「建议收藏」
- Where is your most secretive personality?
猜你喜欢
皕杰报表的下拉框联动

three.js调试工具dat.gui使用
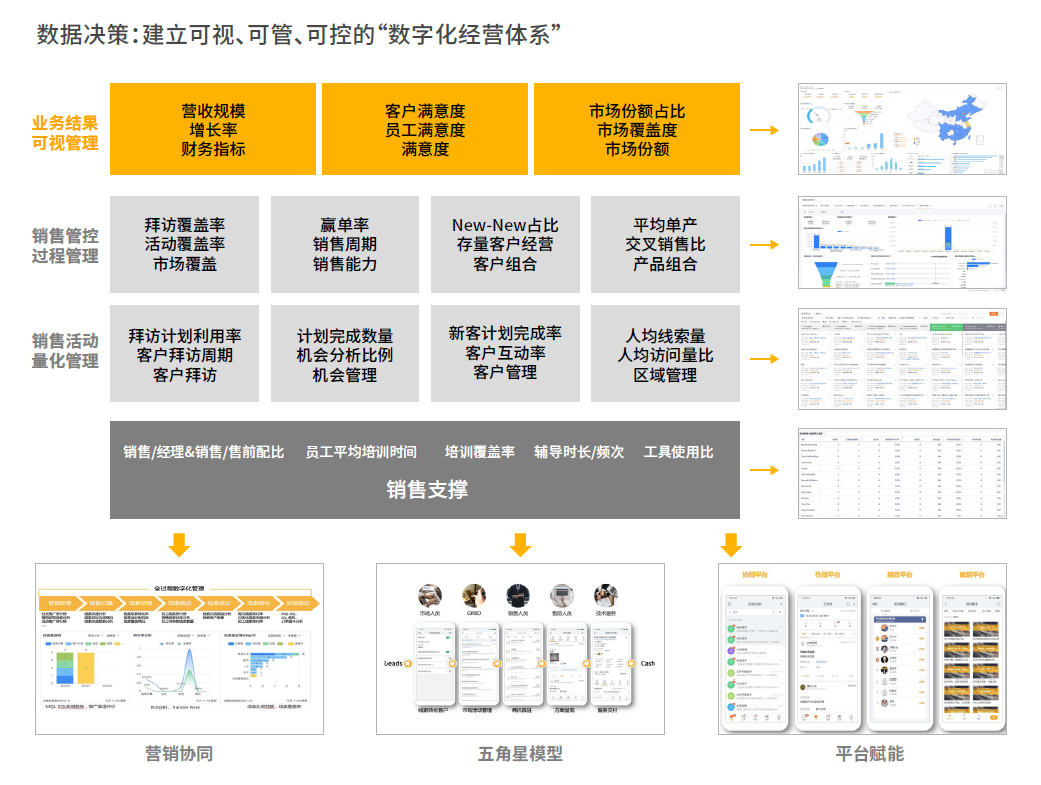
什么是CRM决策分析管理?

Advanced usage of C language

Oracle temporary table space role

The founder of the DFINITY Foundation talks about the ups and downs of the bear market, and where should DeFi projects go?

Complete image segmentation efficiently based on MindSpore and realize Dice!
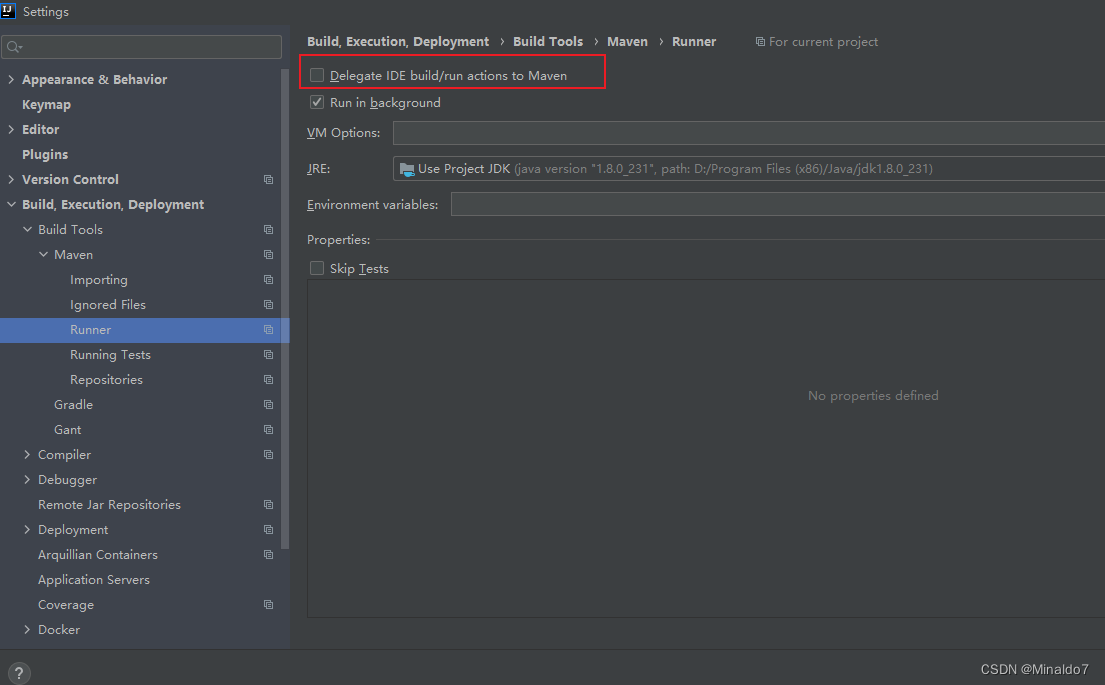
IDEA performs the Test operation, resulting in duplicate data when data is inserted
Egg framework usage (1)
Still looking for a network backup resources?Hurry up to collect the following network backup resource search artifact it is worth collecting!
随机推荐
茄子科技CEO仇俊:以用户为中心,做用户真正需要的产品
PHP operation mangoDb
Keil升级到AC6后,到底有哪些变化?
After Keil upgrades to AC6, what changes?
ffmpeg drawtext add text watermark
基于MindSpore高效完成图像分割,实现Dice!
无题二
MySQL之数据视图
three.js debugging tool dat.gui use
C语言的高级用法
正则表达式replaceFirst()方法具有什么功能呢?
Jenkins使用手册(2) —— 软件配置
What is SPL?
技术干货 | 基于 MindSpore 实现图像分割之豪斯多夫距离
Bias lock/light lock/heavy lock lock is healthier. How is locking and unlocking accomplished?
【Unity】【UGUI】【在屏幕上显示文本】
语音社交软件开发——充分发挥其价值
Microservice Technology Stack
企业的数字化转型到底是否可以买来?
微服务 技术栈