当前位置:网站首页>搜索与图论:Dijkstra求最短路 I—Dijkstra(最短路径)
搜索与图论:Dijkstra求最短路 I—Dijkstra(最短路径)
2022-06-11 15:55:00 【奋斗吧!骚年!】
题目:AcWing 849. Dijkstra求最短路 I
给定一个 n 个点 m 条边的有向图,图中可能存在重边和自环,所有边权均为正值。
请你求出 1 号点到 n 号点的最短距离,如果无法从 1 号点走到 n 号点,则输出 −1。
输入格式
第一行包含整数 n 和 m。
接下来 m 行每行包含三个整数 x,y,z,表示存在一条从点 x 到点 y 的有向边,边长为 z。
输出格式
输出一个整数,表示 1 号点到 n 号点的最短距离。
如果路径不存在,则输出 −1。
数据范围
1≤n≤500,
1≤m≤105,
图中涉及边长均不超过10000。
输入样例:
3 3
1 2 2
2 3 1
1 3 4
输出样例:
3
朴素迪杰斯特拉算法:
进行n次循环,
1.第一步:找到一个没有确定的点,并且距离起点最近(贪心)证明略
2.第二步:将其余所有点与当前点进行更新距离,因为很多点可以通过该点到达起点。
3.第三步:将该点标记为确定的点
#include <iostream>
#include <cstring>
using namespace std;
const int N = 510;
int g[N][N]; // 邻接矩阵
int dist[N]; // 最短路径
bool st[N]; // 判断点是否最短
int n,m;
int dijkstra()
{
memset(dist,0x3f,sizeof(dist));
dist[1]=0; // 第一个点的距离为0
for(int i=0;i<n-1;i++)
{
int t=-1;
for(int j=1;j<=n;j++) // 找到一个没有确定的点,且离起点最近(贪心)
if(!st[j]&&(t==-1||dist[t]>dist[j]))
t=j;
for(int j=1;j<=n;j++) // 将所有点与当前点更新距离
dist[j]=min(dist[j],dist[t]+g[t][j]);
st[t]=true; // 将当前点置为确定的点
}
if(dist[n]==0x3f3f3f3f)return -1;
return dist[n];
}
int main()
{
cin>>n>>m;
memset(g,0x3f,sizeof(g)); // 初始化距离
while(m--)
{
int a,b,c;
cin>>a>>b>>c;
g[a][b]=min(g[a][b],c); // 保证邻接矩阵是最短距离
}
int k=dijkstra();
cout<<k<<endl;
return 0;
}
边栏推荐
- Hands on, how should selenium deal with pseudo elements?
- Import data: GS_ restore or MERGE INTO? See which one suits you better
- MSDN download win11 method, simple and easy to operate
- Nat Commun|語言模型可以學習複雜的分子分布
- 前沿科技探究DeepSQL:库内AI算法
- Opengauss AI capability upgrade to create a new AI native database
- Go language slice
- AGC安全规则是如何简化用户授权和验证请求
- 使用Cloud DB构建APP 快速入门-快游戏篇
- Using cloud DB to build app quick start -server
猜你喜欢
How does the taskbar under the computer display open programs

Elk enterprise log analysis system

Nat Common | le Modèle linguistique peut apprendre des distributions moléculaires complexes

Code farming essential SQL tuning (Part 1)

3000 words to teach you how to use mot

Discussion on opengauss parallel decoding

jdbc调试错误,求指导
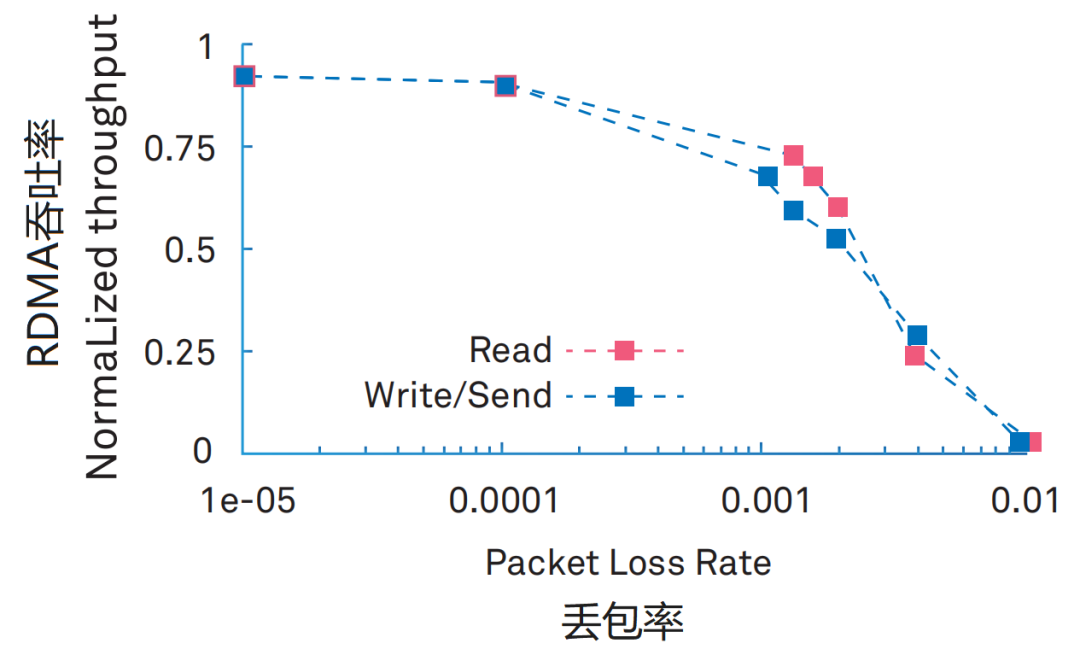
再聊数据中心网络

Project workspace creation steps - Zezhong ar automated test tool

带你深度了解AGC云数据库
随机推荐
使用Cloud DB构建APP 快速入门-快应用篇
laravel 8 使用passport 进行Auth验证及颁发token
Tianjin Port coke wharf hand in hand map flapping software to visually unlock the smart coke port
GO语言数组和切片的区别
WGet command use
如何优化 Compose 的性能?通过「底层原理」寻找答案 | 开发者说·DTalk
带你深度了解AGC云数据库
Hands on, how should selenium deal with pseudo elements?
DHCP协议实例化分析
无心剑英汉双语诗001. 《春游》
Overview and operation of database dense equivalent query
AI tool for cutting-edge technology exploration: analog detection
PostgreSQL create database
How to predict SQL statement query time?
向数据库导入数据?试试COPY FROM STDIN语句
Db4ai: database driven AI
Go language - value types and reference types
How the autorunner automated test tool creates a project -alltesting | Zezhong cloud test
How does the taskbar under the computer display open programs
Open the door of the hybrid cloud market, Lenovo xcloud's way to break the situation