当前位置:网站首页>[matlab] matrix
[matlab] matrix
2022-06-12 23:54:00 【No card, no change】
matrix
zeros function
Produce all 0 matrix , Zero matrix .
Invocation format :
- zeros(m): produce m×m The zero matrices of .
- zeros(m, n): produce m×n The zero matrices of .
- zeros(size(A)): Generation and matrix A A zero matrix of the same size .
The following functions are called in the same way .
ones function
Produce all 1 matrix , Unitary matrix .
eye function
The resulting diagonal is 1 Matrix . When the matrix is a square matrix , Get an identity matrix .
rand function
produce (0, 1) Interval uniformly distributed random matrix .
randn function
randn function : The average production is 0, The variance of 1 Standard normal distribution random matrix .
randi function
randi() Function to generate uniformly distributed pseudo-random integers , The scope is imin–imax, If not specified imin, The default is 1.
r = randi(imax,n): Generate n×n Matrix ,n If omitted, the 1×1 Matrix
r = randi(imax,m,n): Generate m×n Matrix
r = randi(imax,[m,n]): ditto , usage :r = randi(imax,size(A));
r = randi(imax,m,n,p,…): Generate m×n×p×… Matrix
r = randi(imax,[m,n,p,…]): ditto
r = randi([imin,imax],…): Specifies the imin, Other parameters are the same as above
application 1
First generation 5 Order two bit random integer matrix A, The resulting mean is 0.6、 The variance of 0.1 Of 5 Order normal distribution random matrix B, The final validation (A+B)I=IA+BI(I Is the unit matrix ).
- fix(a+(b-a+1)*x): produce [a, b] Random integers uniformly distributed on an interval .
- μ \mu μ+ σ \sigma σx: The mean value is μ \mu μ、 The variance of σ 2 \sigma^2 σ2 The random number .
A = fix(10+(99-10+1)*rand(5));
B = 0.6+sqrt(0.1)*randn(5);
C = eye(5);
(A+B)*C == C*A + B*C
give the result as follows :
ans =
5×5 logical Array
1 1 1 1 1
1 1 1 1 1
1 1 1 1 1
1 1 1 1 1
1 1 1 1 1
magic function
n The first order magic cube array consists of 1,2,3,…,n2 common n2 An integer makes up , And every line 、 Each column and main 、 On the sub diagonal n The sum of the two elements is equal .
n The sum of the elements in each row and column of the first-order magic cube array is (1+2+3+…+n2)/n=(n+n3)/2.MATLAB function magic(n) Generate a specific Magic Cube .
M = magic(8);
sum(M(1, :)) % 260
sum(M(:, 1)) % 260
Add up sum Usage of
sum function
Call form :
- sum(A): Sum each column , Returns a row vector consisting of the sum of each column .
- sum(A, 1): And sum(A) Equivalent .
- sum(A, 2): Sum each line , Returns a column vector consisting of the sum of each row .
- sum(subA):subA by A The indexer matrix of , Find the sum of all elements in a submatrix .
Usage example :
A = [1 2 3; 4 5 6;7 8 9];
sum(A) % 12 15 18
sum(A, 1) % 12 15 18
sum(A, 2)
% 6
% 15
% 24
sum(A(1:2, 2:3)) % 7 9
sum(A(:)) % 45
Adjoint matrix
MATLAB The function that generates the adjoint matrix is compan§, among p Is the coefficient vector of a polynomial , Higher power coefficients rank first , The lower power coefficient comes next .
for example , Generating polynomials x 3 − 2 x 2 − 5 x + 6 x^3-2x^2-5x+6 x3−2x2−5x+6 The adjoint matrix of .
p = [1 -2 -5 6];
A = compan(p)
give the result as follows :
A =
2 5 -6
1 0 0
0 1 0
sparse matrix
Full storage mode
Sparse storage
Sparse storage only stores the values and positions of non-zero elements of the matrix , Line number and column number .
Be careful , When using sparse storage , The order in which matrix elements are stored does not change , It's also stored in column order .
Conversion between full storage and sparse storage
A=sparse(S): The matrix S Into a sparse storage matrix A.
S=full(A): The matrix A A matrix converted to full storage S.
A = sparse(eye(3)) % Equivalent to speye(3)
full(A)
give the result as follows :
A =
(1,1) 1
(2,2) 1
(3,3) 1
ans =
1 0 0
0 1 0
0 0 1
sparse Other call formats for functions
sparse(m, n): Generate a m × n m×n m×n A sparse matrix in which all elements of are zero .
A = sparse(4, 5);
A(8) = 3;
A(1, 2) = 4;
full(A(1:3, :))
give the result as follows :
ans =
0 4 0 0 0
0 0 0 0 0
0 0 0 0 0
First, all zero sparse matrix is generated through the above calling format , Then the assignment and access operations can be carried out through the assignment and access modes of the full storage mode .
spase(row, col, val):row、col and val Is a vector of equal length , Respectively represents the line number , Column number and corresponding value .
A = sparse([1 2 2], [2 1 4], [4 5 -7])
full(A)
give the result as follows :
A =
(2,1) 5
(1,2) 4
(2,4) -7
ans =
0 4 0 0
5 0 0 -7
spconvert function
The invocation format is :spconvert(A),A A matrix with three columns for several rows or four columns for several rows , The first column represents the row number of each number , The second column represents the column number of each number , The third column represents the real part of each number , The fourth column represents the imaginary part of each number , If all elements of the matrix are real numbers , The fourth column is not required ; so ,A Each row of the matrix represents a non-zero element , The number of rows is the number of non-zero elements in the sparse matrix .
A = [2 2 1; 2 1 -1; 2 4 3]
spconvert(A)
give the result as follows :
A =
2 2 1
2 1 -1
2 4 3
ans =
(2,1) -1
(2,2) 1
(2,4) 3
Banded sparse matrix
[B,d]=spdiags(A): From banded sparse matrix A Extract all non-zero diagonal elements and assign them to the matrix B And the position vectors of these non-zero diagonals d.
A=spdiags(B,d,m,n): A sparse storage matrix that generates a banded sparse matrix A, among m、n Is the number of rows and columns of the original banded sparse matrix , matrix B Of the i The column is the... Of the original banded sparse matrix i A non-zero diagonal , vector d Is the position of all non-zero diagonals of the original banded sparse matrix .
A=[11 0 0 12 0 0; 0 21 0 0 22 0; 0 0 31 0 0 32; 41 0 0 42 0 0; 0 51 0 0 52 0]
[B,d]=spdiags(A)
give the result as follows :
A =
11 0 0 12 0 0
0 21 0 0 22 0
0 0 31 0 0 32
41 0 0 42 0 0
0 51 0 0 52 0
B =
0 11 12
0 21 22
0 31 32
41 42 0
51 52 0
d =
-3
0
3
spdiags(B, d, 5, 6)
give the result as follows :
ans =
(1,1) 11
(4,1) 41
(2,2) 21
(5,2) 51
(3,3) 31
(1,4) 12
(4,4) 42
(2,5) 22
(5,5) 52
(3,6) 32
We can also generate a banded sparse matrix by first generating a fully stored matrix and then converting it to a sparse matrix :
B = diag([11 21 31 42 52 0]) + diag([12 22 32], 3) + diag([41 51 0], -3);
B = B(1:end-1, :)
sparse(B)
give the result as follows :
B =
11 0 0 12 0 0
0 21 0 0 22 0
0 0 31 0 0 32
41 0 0 42 0 0
0 51 0 0 52 0
ans =
(1,1) 11
(4,1) 41
(2,2) 21
(5,2) 51
(3,3) 31
(1,4) 12
(4,4) 42
(2,5) 22
(5,5) 52
(3,6) 32
First use diag Function to build a square matrix , Add the square matrices to get the completely stored matrix , call sparse Make it sparse .
Be careful :
spdiags(B,d,m,n) In the format m、n The size relationship of determines how to use the matrix B Fill in :
Conclusion :
- When m≤n when , The diagonal below the main diagonal ( That is, the diagonal -1:-n+1) When data filling , from B A column of a matrix Top to bottom DE value ; And the diagonal above the main diagonal (1:n-1) When filling elements , from B A column of From bottom to top DE value .
- When m>n when , When data is filled in the diagonal below the main diagonal , from B A column of a matrix From bottom to top DE value ; When the diagonal above the main diagonal is filled with elements , from B A column of Top to bottom DE value .
See the following example :
A = reshape(1:15, 5, 3);
B = spdiags(A,[-2 0 2], 5, 5);
C = spdiags(A,[-2 0 2], 5, 6);
D = spdiags(A,[-2 0 2], 5, 4);
A
BB = full(B)
CC = full(C)
DD = full(D)
A =
1 6 11
2 7 12
3 8 13
4 9 14
5 10 15
BB =
6 0 13 0 0
0 7 0 14 0
1 0 8 0 15
0 2 0 9 0
0 0 3 0 10
CC =
6 0 11 0 0 0
0 7 0 12 0 0
3 0 8 0 13 0
0 4 0 9 0 14
0 0 5 0 10 0
DD =
6 0 13 0
0 7 0 14
1 0 8 0
0 2 0 9
0 0 3 0
speye function
speye(n): return n Order unit matrix .
speye(m, n): return m × n m×n m×n Unit matrix of .
application
The storage and operation of sparse matrix through sparse storage can improve the efficiency of operation , This is the most important reason why we use sparse matrices .

k1 = [1; 1; 2; 1; 0];
k2 = [2; 4; 6; 6; 1];
k3 = [0; 3; 1; 4; 2];
B = [k1 k2 k3];
d = [-1 0 1];
A = spdiags(B, d, 5, 5);
full(A)
b = [0; 3; 2; 1; 5];
x = A\b
give the result as follows :
ans =
2 3 0 0 0
1 4 1 0 0
0 1 6 4 0
0 0 2 6 2
0 0 0 1 1
x =
-0.1667
0.1111
2.7222
-3.6111
8.6111
边栏推荐
- Leetcode 2200. Find all k nearest neighbor subscripts in the array (yes, one pass)
- leaflet中如何通过透明度控制layerGroup的显示隐藏
- Memory address mapping of u-boot
- Enterprise wechat H5_ Authentication, H5 application web page authorization login to obtain identity
- Day 3 of jsbom and DOM learning
- How leaflet gracefully displays the bubble window of overlapping points
- How does idea switch the interface to Chinese
- MySql索引
- How to pass the PMP review?
- VS2015 DLIB 1916 USER_ ERROR__ inconsistent_ build_ configuration__ see_ dlib_ faq_ 1 USER_ ERROR__ inconsiste
猜你喜欢

【Matlab】二维曲线

PLC也能制作小游戏----Codesys编写猜数字小游戏

How to control the display and hiding of layergroup through transparency in leaflet

2022 electrician (elementary) operation certificate examination question bank and online simulation examination

Based on three JS offshore wind power digital twin 3D effect
How to make maputnik, a vector tile matching artifact, support GeoServer

Accelerating with Dali modules
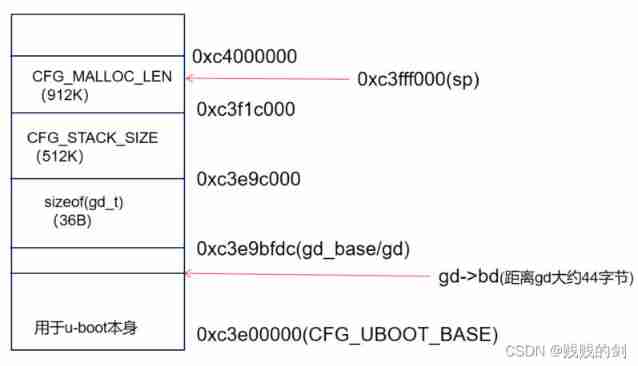
Start of u-boot_ Armboot analysis (I)

Leetcode 2200. Find all k nearest neighbor subscripts in the array (yes, one pass)

OSM map local publishing - how to generate vector maps of provinces and cities
随机推荐
Is divicon still used in leaflet in H5 era?
21 Chundong University blasting safety online peacetime operation 123 [standard answer]
Teach you how to grab ZigBee packets through cc2531 and parse encrypted ZigBee packets
妙才周刊 - 5
數組
PMP renewal | PDU specific operation diagram
MySQL index
2022起重机械指挥上岗证题目模拟考试平台操作
Summary of the lowest level error types in PHP
[leetcode] understanding and usage of map[key]+
[SciPy optimization tutorial] v. quick solution of univariate function optimization
Online examination questions for September examination of financial management
Software development tools [3] theoretical basis of software development tools
The PMP examination time in March 2022 is set -- "March 27"
How does the PMP handle the withdrawal?
M_8:设计消息队列存储消息数据的 MySQL 表格
OSM地图本地发布-如何生成各省市矢量地图
36 krypton's debut | "osogena" won nearly ten million angel rounds of financing. The original DLR scientists of German Aerospace Research and development system modeling and simulation CAE software PA
2022年R2移动式压力容器充装考试题及在线模拟考试
Start of u-boot_ Armboot analysis (II)