Convex optimization notes

Simple convex optimization notes

Convex functions and convex sets

• The region above the convex function is a convex set
• The region above the function is a convex set , Then the function is convex

convex set

aggregate $C$ The line segments between any two points are in the set $C$ in , It's called a collection $C$ For convex sets
$$\begin{gathered} \forall x_1,x_2\in C,\theta \in [0,1] \\ be\theta x_1+(1-\theta )x_2\in C \end{gathered}$$
expand
$$\begin{gathered} \forall x_1,...,x_k\in C,{\theta }_i\in [0,1]And\sum {\theta }_i=1 \\ be\sum {\theta }_i{x}_i\in C \end{gathered}$$

A convex polygon is a convex set , Boundary missing is not a convex set

Hyperplane and half space

hyperplane

$$\{x|a^{T}x=b\}$$

Half space

$$\begin{gathered} \{x|a^{T}x\le b\} \\ \{x|a^{T}x\ge b\} \end{gathered}$$

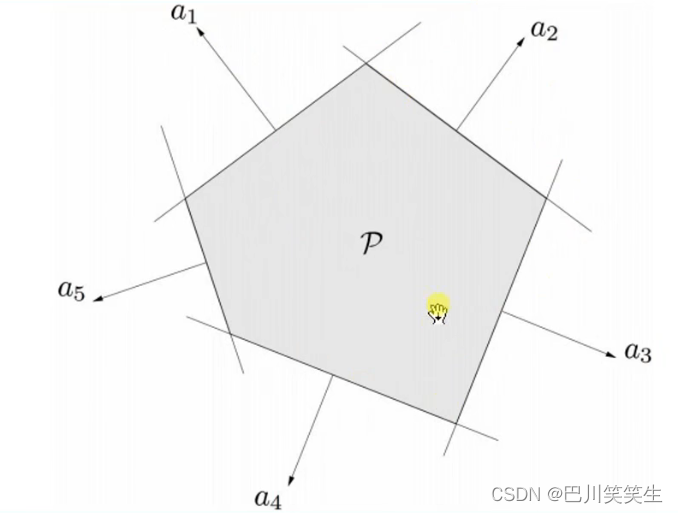
Polyhedron

A polyhedron is the intersection of a finite half space and a hyperplane
$$P=\{x|a_j^{T}x\le b_j,c_i^{T}x=d_i\}$$
Affine set （ Such as hyperplane , A straight line ）, ray , Line segment , Half spaces are polyhedrons

A polyhedron is a convex set

A bounded polyhedron is called a polyhedron

Keep convexity operation

• Set intersection operation

Proof of definition

• Affine transformation
  • Telescopic
  • translation
  • Projection

$$\begin{gathered} f(x)=Ax+b,A\in R^{m\times n},b\in R^m \\ f:R^n\to R^{m}f(S)=\{f(x)|x\in S\} \\ SbyConvexSet\to f(S)byConvexSet \\ f(S)byConvexSet\to SbyConvexSet \end{gathered}$$

• Perspective transformation

The perspective function scales the vector （ standard ） Let the components of the last dimension be discarded together
$$P:R^{n+1}\to R^n,P(z,t)=z/t$$

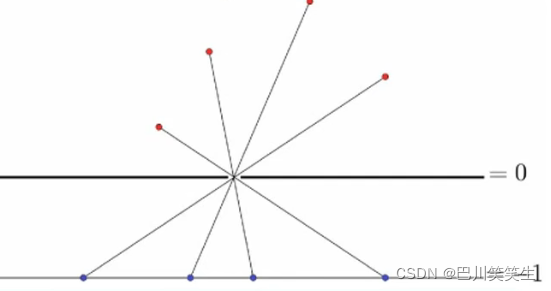
• Projective transformation （ Linear fractional transformation ）

Compound of perspective and affine
$$\begin{gathered} g:R^n\to R^{n+1} \\ g(x)=\left[\begin{array}{c}A\\ c^T\end{array}\right]x+\left[\begin{array}{c}b\\ d\end{array}\right] \\ A\in R^{m\times n},b\in R^m,c\in R^n,d\in R \end{gathered}$$
Definition $f$ Is a linear fractional function
$$\begin{gathered} f(x)=\frac{(Ax+b)}{c^{T}x+d} \\ domf=\{x|c^{T}x+d>0\} \end{gathered}$$
if $c=0,d>0$ be $f$ Is an ordinary affine function

Split hyperplane

set up $C$ and $D$ For two disjoint convex sets , Then there is a hyperplane $P$,$P$ Can be $C$ and $D$ Separate
$$\forall x\in C,a^{T}x\le bAnd\forall x\in D,a^{T}x\ge b$$

Note that you can take the equal sign

Converse proposition

If two convex sets $C$ and $D$ The divided hyperplane exists ,$C$ and $D$ Disjoint is a false proposition

Strengthen the conditions

If at least one of the two convex sets is open , Then if and only if there is a split hyperplane , They don't intersect

Split hyperplane construction

distance

The distance between two sets is the shortest distance between two sets

structure

Make a distance perpendicular to

Supporting hyperplanes

A collection of $C$,$x_0$ by $C$ Points on the border . If exist $a\ne 0$, Satisfied with any $x\in C$, There are $a^{T}x\le a^T{x}_0$ establish , Is called hyperplane $\{x|a^{T}x=a^T{x}_0\}$ For collection $C$ At point $x_0$ Support hyperplane at

There is a supporting hyperplane at any point on the boundary of a convex set

conversely , If a closed non hollow （ The inner point is not empty ） aggregate , There is a supporting hyperplane at any point on the boundary , Then the set is convex

Convex function

If the function $f$ Domain of definition $domf$ For convex sets , And meet
$$\forall x,y\in domf,0\le \theta \le 1Yesf(\theta x+(1-\theta )y)\le \theta f(\theta )+(1-\theta )f(y)$$

First order differentiable

if $f$ First order differentiable , The function $f$ Is a convex function if and only if $f$ The domain of definition $domf$ Is a convex set and
$$\forall x,y\in domf,f(y)\ge f(x)+▽f(x{)}^T(y-x)$$

For convex functions , The essence of the first-order Taylor approximation is the global estimation of the function

On the contrary, if a function's first-order Taylor approximation is always its global estimation , Then the function is convex

Second order differentiability

If the function $f$ Second order differentiability , The function $f$ Is a convex function if and only if $domf$ For convex sets , And
$${▽}^{2}f(x)\succ =0$$
if $f$ For a function of one variable , The above formula indicates that the second derivative is greater than or equal to $0$

if $f$ Is a multivariate function , The above formula represents the positive semidefinite of the second derivative Hessian matrix

Example

• $e^{ax}$
• $x^a,x\in R_{+},a\ge 1ora\le 0$
• $-logx$
• $xlogx$
• $||x|{|}_p$
  • $max(x_1,...,x_n)$
  • $x^2/a,a>0$
  • $log(e^{x_1+...+e^{x_n}})$

Shangjing map

function $f$ The image is defined as $\{(x,f(x))|x\in domf\}$
function $f$ The context map of is defined as
$$epif=\{(x,t)|x\in domf,f(x)\le t\}$$

Convex functions and convex sets

A function is a convex function , If and only if its context graph is a convex set
A function is a concave function , If and only if its set is subconvex
$$hypof=\{(x,t)|t\le f(x)\}$$

Jason inequality

$f$ Is a convex function
$$f(\theta x+(1-\theta )y)\le \theta f(x)$$
$$\begin{gathered} if{\theta }_1...{\theta }_k\ge 0,{\theta }_1+...+{\theta }_k=1 \\ bef({\theta }_1{x}_1+...+{\theta }_k{x}_k)\le {\theta }_{1}f(x_1)+...+{\theta }_{k}f(x_k) \end{gathered}$$
$$\begin{gathered} ifp(x)\ge 0stayS\subseteq domf,{\int }_{S}p(x)dx=1 \\ bef({\int }_{S}p(x)xdx)\le {\int }_{S}f(x)p(x)dx \\ orf(Ex)\le E(f(x)) \end{gathered}$$
It can be proved by Jason inequality
$$D(p||q)=\sum p(x)log\frac{p(x)}{q(x)}=E_{p(x)}log\frac{p(x)}{q(x)}\ge 0$$
wait

Operators that preserve the convexity of functions

• Nonnegative weighted sum
  $$f(x)=w_1{f}_1(x)+...+w_n{f}_n(x)$$
• Compound with affine function
  $$g(x)=f(Ax+b)$$
• Point by point maximum , Pointwise supremum
  $$\begin{gathered} f(x)=max(f_1(x),...,f_n(x)) \\ f(x)=\underset{y\in A}{\sup }g(x,y) \end{gathered}$$

The pointwise supremum function of the function corresponds to the intersection of the boundary graph on the function

Convex optimization

The basic form of optimization problem

$$\begin{gathered} mostSmallturn{f}_0(x),x\in R^n \\ Noetc.typeaboutbeam{f}_i(x)\le 0,i=1...m \\ etc.typeaboutbeam{h}_i(x)=0,j=1...p \\ nothingaboutbeamoptimalturnm=p=0 \end{gathered}$$
$$\begin{gathered} optimalturnasktopicOfDomainD=\bigcap _{i=1}^{m}dom{f}_i\cap \bigcap _{j=1}^{p}dom{h}_j \\ canThat\text{'}s\; okspot（Explain）x\in DAndfullfootaboutbeamstripPieces\; of \\ canThat\text{'}s\; okDomain,theYescanThat\text{'}s\; okspotSetclose \end{gathered}$$
$$\begin{gathered} mostoptimalturnvalue{p}^{\ast }=inf\{f_0(x)|f_i(x)\le 0,i=1...m,h_j(x)=0,j=1...p\} \\ mostoptimalturnExplain{p}^{\ast }=f_0(x^{\ast }) \end{gathered}$$

The basic form of convex optimization problem

$$\begin{gathered} f_i(x)byConvexLetterCount \\ {h}_j(x)byImitationshootLetterCount \end{gathered}$$
Important nature

• The feasible region is a convex set
• The local optimal solution is the global optimal solution

The dual problem

Lagrange function

$$L(x,\lambda ,\upsilon )=f_0(x)+\sum {\lambda }_i{f}_i(x)+\sum {\upsilon }_j{h}_j(x)$$
To fix $x$, Lagrange function $L(x,\lambda ,\upsilon )$ For about $\lambda$ and $\upsilon$ The affine function of

Lagrange dual function

$$\begin{gathered} g(\lambda ,\upsilon )=\underset{x\in D}{\inf }L(x,\lambda ,\upsilon )=\underset{x\in D}{\inf }(f_0(x)+\sum {\lambda }_i{f}_i(x)+\sum {\upsilon }_j{h}_j(x)) \\ ifnothingNextindeedworldsetThe\; righteousg(\lambda ,\upsilon )=-\infty \end{gathered}$$
By definition, there are ： Yes $\forall \lambda \ge 0,\forall \upsilon$, The original optimization problem has the optimal value $p^{\ast }$, be
$$g(\lambda ,\upsilon )\le p^{\ast }$$
further , Lagrange dual function is concave function

hypothesis $x_0$ Is not workable , There is $f_i(x)>0$, select ${\lambda }_i\to \infty$, For other multipliers ${\lambda }_i=0,j\ne i$
hypothesis $x_0$ feasible , Then there are $f_i(x)\le 0,i=1...m$, Make ${\lambda }_i=0,i=1...m$
Yes
$$\underset{\lambda \ge 0}{\sup }L(x,\lambda )=\underset{\lambda \ge 0}{\sup }(f_0(x)+\sum {\lambda }_i{f}_i(x))=\{\begin{array}{c}{f}_0(x),f_i(x)<0\\ \infty ,other\end{array}$$

The original problem is ${\inf }_x{f}_0(x)$ Turn into ${\inf }_x{\sup }_{\lambda \ge 0}L(x,\lambda )$
The dual problem is to find the maximum value of the dual function , namely
$$\underset{\lambda \ge 0}{\sup }\underset{x}{\inf }L(x,\lambda )$$
and
$$\underset{\lambda \ge 0}{\sup }\underset{x}{\inf }L(x,\lambda )\le \underset{x}{\inf }\underset{\lambda \ge 0}{\sup }L(x,\lambda )$$

Strong dual condition

The maximum value of the dual function is the minimum value of the original problem
$$\begin{gathered} f_0(x^{\ast })=g({\lambda }^{\ast }+{\upsilon }^{\ast }) \\ =\underset{x}{\inf }(f_0(x)+\sum {\lambda }_i^{\ast }{f}_i(x)+\sum {\upsilon }_j^{\ast }{h}_j(x)) \\ \le f_0(x^{\ast })+\sum {\lambda }_i^{\ast }{f}_i(x^x)+\sum {\upsilon }_j^{\ast }{h}_j(x^{\ast }) \\ \le f_0(x^{\ast }) \end{gathered}$$
Conditions
$$\begin{gathered} f_i(x^{\ast })\le 0 \\ {h}_i(x^{\ast })=0 \\ {\lambda }_i^{\ast }\ge 0 \\ {\lambda }_i^{\ast }{f}_i(x^{\ast })=0 \\ i=1...m \\ ▽f_0(x^{\ast })+\sum {\lambda }_i^{\ast }▽f_i(x^x)+\sum {\upsilon }_j^{\ast }▽h_j(x^{\ast })=0 \end{gathered}$$