当前位置:网站首页>Random finite set RFs self-study notes (6): an example of calculation with the formula of prediction step and update step
Random finite set RFs self-study notes (6): an example of calculation with the formula of prediction step and update step
2022-07-28 19:14:00 【Learn something】
There are so many derivation formulas written above , I always feel that it is not intuitive and impressive , Personally, I think that looking at specific examples can quickly understand how this thing works , I'll try to describe this example .
Start with the simplest example : linear equation , Normal distribution , One dimensional scalar .
Some symbols need to be explained : p − ( x k ) p^-(x_k) p−(xk) It means No k k k A priori value of time , p + ( x k ) p^+(x_k) p+(xk) It means No k k k Posterior value of time . in addition , p ( x k ∣ z 1 : k − 1 ) p(x_k|z_{1:k-1}) p(xk∣z1:k−1) It also means k k k A priori value of time , and p − ( x k ) p^-(x_k) p−(xk) identical ; p ( x k ∣ z 1 : k ) p(x_k|z_{1:k}) p(xk∣z1:k) It also means k k k Posterior value of time , and p + ( x k ) p^+(x_k) p+(xk) identical . there z 1 : k z_{1:k} z1:k The representation is based on 1 Moment to k All the time z z z Information .
set up
0 A posteriori probability of time : p + ( x 0 ) p^+(x_0) p+(x0)—— Subjective guess
1 A priori probability of time : p − ( x 1 ) = p ( x 1 ∣ z 0 ) = N ( x 1 ; 0.5 , 0.2 ) p^-(x_1)=p(x_1|z_0)=N(x_1;0.5,0.2) p−(x1)=p(x1∣z0)=N(x1;0.5,0.2)
Motion models :
x k = f ( x k − 1 ) + q k = x k − 1 + q k x_k=f(x_{k-1})+q_k=x_{k-1}+q_k xk=f(xk−1)+qk=xk−1+qk, among , q k ∼ N ( 0 , 0.35 ) q_k\sim N(0,0.35) qk∼N(0,0.35)
Then you can predict π k ( x k ∣ x k − 1 ) = N ( x k ; x k − 1 , 0.35 ) \pi_k(x_k|x_{k-1})=N(x_k;x_{k-1},0.35) πk(xk∣xk−1)=N(xk;xk−1,0.35)—— Based on k − 1 k-1 k−1 Time information to infer k k k The distribution of time , Isn't this prediction ?
detection probability : P D = 0.9 P^D=0.9 PD=0.9, Here we use constants
Theoretical measurement model :
o k = h ( x k ) + r k = x k + r k o_k=h(x_k)+r_k=x_k+r_k ok=h(xk)+rk=xk+rk, among , r k ∼ N ( 0 , 0.2 ) r_k\sim N(0,0.2) rk∼N(0,0.2)
Get the theoretical likelihood g k ( o k ∣ x k ) = N ( o k ; x k , 0.2 ) g_k(o_k|x_k)=N(o_k;x_k,0.2) gk(ok∣xk)=N(ok;xk,0.2)
Clutter intensity : λ ( c ) = { 0.4 ∣ c ∣ ≤ 4 0 o t h e r s \lambda(c)=\left\{\begin{matrix} 0.4 &|c|\leq4 \\ 0& others \end{matrix}\right. λ(c)={ 0.40∣c∣≤4others be λ c = 0.4 ∗ 8 = 3.2 \lambda_c=0.4*8=3.2 λc=0.4∗8=3.2, be f c ( c ) = { 1 / 8 ∣ c ∣ ≤ 4 0 o t h e r s f_c(c)=\left\{\begin{matrix} 1/8 &|c|\leq4 \\ 0& others \end{matrix}\right. fc(c)={ 1/80∣c∣≤4others
Observed value : z 1 = [ − 1.3 , 1.7 ] , z 2 = [ 1.3 ] , z 3 = [ − 0.3 , 2.3 ] z_1=[-1.3,1.7],z_2=[1.3],z_3=[-0.3,2.3] z1=[−1.3,1.7],z2=[1.3],z3=[−0.3,2.3] And m 1 = 2 , m 2 = 1 , m 3 = 2 m_1=2,m_2=1,m_3=2 m1=2,m2=1,m3=2
Generally speaking, we should first base on the posterior of subjective conjecture p + ( x 0 ) p^+(x_0) p+(x0) Yes 1 Make predictions all the time , And then combine 1 Observations at the moment z 1 z_1 z1 Conduct 1 Update at any time , To get 1 Posterior value of time . But here , The known conditions have been given 1 A priori value of time , therefore , The next thing to do here is to combine z 1 z_1 z1 Conduct 1 Update at any time , Get the posterior value .
1 Update step formula at time p ( x k ∣ z 1 : k ) = ∑ θ 1 : k p ( x k ∣ z 1 : k , θ 1 : k ) p ( θ 1 : k ∣ z 1 : k ) = p ( x 1 ∣ z 1 ) = ∑ θ 1 p ( x 1 ∣ θ 1 , z 1 ) p ( θ 1 ∣ z 1 ) = p ( x 1 ∣ θ = 0 , z 1 ) p ( θ = 0 ∣ z 1 ) + p ( x 1 ∣ θ = 1 , z 1 ) p ( θ = 1 ∣ z 1 ) + p ( x 1 ∣ θ = 2 , z 1 ) p ( θ = 2 ∣ z 1 ) p(x_k|z_{1:k})=\sum_{\theta_{1:k}}p(x_k|z_{1:k},\theta_{1:k})p(\theta_{1:k}|z_{1:k})\\=p(x_1|z_{1})=\sum_{\theta_1}p(x_1|\theta_1,z_1)p(\theta_1|z_1)\\=p(x_1|\theta=0,z_1)p(\theta=0|z_1)\\+p(x_1|\theta=1,z_1)p(\theta=1|z_1)\\+p(x_1|\theta=2,z_1)p(\theta=2|z_1) p(xk∣z1:k)=θ1:k∑p(xk∣z1:k,θ1:k)p(θ1:k∣z1:k)=p(x1∣z1)=θ1∑p(x1∣θ1,z1)p(θ1∣z1)=p(x1∣θ=0,z1)p(θ=0∣z1)+p(x1∣θ=1,z1)p(θ=1∣z1)+p(x1∣θ=2,z1)p(θ=2∣z1) Then calculate each item separately : Probability and weight . It can be seen that , Probability is obviously to use Bayesian formula —— The same as Bayesian filtering ; How to calculate the weight ?
Calculate the probability p ( x 1 ∣ θ = 0 , z 1 ) = p ( x 1 ∣ z 0 ) p ( θ = 0 , z 1 ∣ x 1 ) p ( θ = 0 , z 1 ) = η p ( x 1 ∣ z 0 ) p ( θ = 0 , z 1 ∣ x 1 ) p(x_1|\theta=0,z_1)=\frac{p(x_1|z_0)p(\theta=0,z_1|x_1)}{p(\theta=0,z_1)}\\=\eta p(x_1|z_0)p(\theta=0,z_1|x_1) p(x1∣θ=0,z1)=p(θ=0,z1)p(x1∣z0)p(θ=0,z1∣x1)=ηp(x1∣z0)p(θ=0,z1∣x1) there p ( x 1 ∣ z 0 ) p(x_1|z_0) p(x1∣z0) Is a priori , p ( θ = 0 , z 1 ∣ x 1 ) p(\theta=0,z_1|x_1) p(θ=0,z1∣x1) Is likelihood probability —— Likelihood is calculated from the measurement model p ( θ = 0 , z 1 ∣ x 1 ) = p ( θ = 0 , m 1 , z 1 ∣ x 1 ) = p ( θ = 0 , m 1 ∣ x 1 ) p ( z 1 ∣ x 1 , θ = 0 , m 1 ) p(\theta=0,z_1|x_1)=p(\theta=0,m_1,z_1|x_1)\\=p(\theta=0,m_1|x_1)p(z_1|x_1,\theta=0,m_1) p(θ=0,z1∣x1)=p(θ=0,m1,z1∣x1)=p(θ=0,m1∣x1)p(z1∣x1,θ=0,m1) and p ( θ = 0 , m 1 ∣ x 1 ) = ( 1 − P D ) P o ( m 1 ; λ c ) p ( z 1 ∣ x 1 , θ = 0 , m 1 ) = ∏ i = 1 m 1 f c ( z i ) p(\theta=0,m_1|x_1)=(1-P^D)Po(m_1;\lambda_c)\\p(z_1|x_1,\theta=0,m_1)=\prod_{i=1}^{m_1}f_c(z^i) p(θ=0,m1∣x1)=(1−PD)Po(m1;λc)p(z1∣x1,θ=0,m1)=i=1∏m1fc(zi) The former is weight , The latter is probability . What we get in this way is p ( z , m 1 , θ = 0 ∣ x ) p(z,m_1,\theta=0|x) p(z,m1,θ=0∣x), And you have to multiply by η p ( x 1 ∣ z 0 ) \eta p(x_1|z_0) ηp(x1∣z0) To get it p ( x 1 ∣ θ = 0 , z 1 ) p(x_1|\theta=0,z_1) p(x1∣θ=0,z1) The value of is assumed θ = 0 \theta=0 θ=0 A posteriori probability of , But this posterior probability needs to be multiplied by a corresponding weight p ( θ = 0 ∣ z 1 ) p(\theta=0|z_1) p(θ=0∣z1) Talent , As a contribution to the final posterior . namely p ( x 1 ∣ θ = 0 , z 1 ) p ( θ = 0 ∣ z 1 ) = p ( x 1 ∣ θ = 0 , m 1 , z 1 ) p ( θ = 0 , m 1 ∣ z 1 ) = η p ( x 1 ∣ z 0 ) p ( θ = 0 , z 1 ∣ x 1 ) p ( θ = 0 , m 1 ∣ z 1 ) = η p ( x 1 ∣ z 0 ) p ( θ = 0 , m 1 ∣ x 1 ) p ( z 1 ∣ x 1 , θ = 0 , m 1 ) p ( θ = 0 , m 1 ∣ z 1 ) = η p ( x 1 ∣ z 0 ) ( 1 − P D ) P o ( m 1 ; λ c ) ∏ i = 1 m 1 f c ( z i ) p ( θ = 0 , m 1 ∣ z 1 ) p(x_1|\theta=0,z_1)p(\theta=0|z_1)\\=p(x_1|\theta=0,m_1,z_1)p(\theta=0,m_1|z_1)\\=\eta p(x_1|z_0)p(\theta=0,z_1|x_1)p(\theta=0,m_1|z_1)\\=\eta p(x_1|z_0)p(\theta=0,m_1|x_1)p(z_1|x_1,\theta=0,m_1)p(\theta=0,m_1|z_1)\\=\eta p(x_1|z_0)(1-P^D)Po(m_1;\lambda_c)\prod_{i=1}^{m_1}f_c(z^i)p(\theta=0,m_1|z_1) p(x1∣θ=0,z1)p(θ=0∣z1)=p(x1∣θ=0,m1,z1)p(θ=0,m1∣z1)=ηp(x1∣z0)p(θ=0,z1∣x1)p(θ=0,m1∣z1)=ηp(x1∣z0)p(θ=0,m1∣x1)p(z1∣x1,θ=0,m1)p(θ=0,m1∣z1)=ηp(x1∣z0)(1−PD)Po(m1;λc)i=1∏m1fc(zi)p(θ=0,m1∣z1) One of the problems we face now is : p ( θ = 0 , m 1 ∣ z 1 ) p(\theta=0,m_1|z_1) p(θ=0,m1∣z1) How to find ? What we know before is how to ask p ( θ = 0 , m 1 ∣ x 1 ) p(\theta=0,m_1|x_1) p(θ=0,m1∣x1), It's different from this .
alike , We can deduce the probability under other assumptions p ( x 1 ∣ θ = 1 , z 1 ) p ( θ = 1 ∣ z 1 ) = p ( x 1 ∣ θ = 1 , m 1 , z 1 ) p ( θ = 1 , m 1 ∣ z 1 ) = η p ( x 1 ∣ z 0 ) p ( θ = 1 , z 1 ∣ x 1 ) p ( θ = 1 , m 1 ∣ z 1 ) = η p ( x 1 ∣ z 0 ) p ( θ = 1 , m 1 ∣ x 1 ) p ( z 1 ∣ x 1 , θ = 1 , m 1 ) p ( θ = 1 , m 1 ∣ z 1 ) = η p ( x 1 ∣ z 0 ) P D P o ( m 1 − 1 ; λ c ) 1 m 1 g k ( z 1 ∣ x 1 ) ∏ i = 1 m 1 f c ( z i ) f c ( z 1 ) p ( θ = 1 , m 1 ∣ z 1 ) p(x_1|\theta=1,z_1)p(\theta=1|z_1)\\=p(x_1|\theta=1,m_1,z_1)p(\theta=1,m_1|z_1)\\=\eta p(x_1|z_0)p(\theta=1,z_1|x_1)p(\theta=1,m_1|z_1)\\=\eta p(x_1|z_0)p(\theta=1,m_1|x_1)p(z_1|x_1,\theta=1,m_1)p(\theta=1,m_1|z_1)\\=\eta p(x_1|z_0)P^DPo(m_1-1;\lambda_c)\frac{1}{m_1}g_k(z^1|x_1)\frac{\prod_{i=1}^{m_1}f_c(z^i)}{f_c(z^1)}p(\theta=1,m_1|z_1) p(x1∣θ=1,z1)p(θ=1∣z1)=p(x1∣θ=1,m1,z1)p(θ=1,m1∣z1)=ηp(x1∣z0)p(θ=1,z1∣x1)p(θ=1,m1∣z1)=ηp(x1∣z0)p(θ=1,m1∣x1)p(z1∣x1,θ=1,m1)p(θ=1,m1∣z1)=ηp(x1∣z0)PDPo(m1−1;λc)m11gk(z1∣x1)fc(z1)∏i=1m1fc(zi)p(θ=1,m1∣z1)
the other one p ( x 1 ∣ θ = 2 , z 1 ) p ( θ = 2 ∣ z 1 ) = p ( x 1 ∣ θ = 2 , m 1 , z 1 ) p ( θ = 2 , m 1 ∣ z 1 ) = η p ( x 1 ∣ z 0 ) p ( θ = 2 , z 1 ∣ x 1 ) p ( θ = 2 , m 1 ∣ z 1 ) = η p ( x 1 ∣ z 0 ) p ( θ = 2 , m 1 ∣ x 1 ) p ( z 1 ∣ x 1 , θ = 2 , m 1 ) p ( θ = 2 , m 1 ∣ z 1 ) = η p ( x 1 ∣ z 0 ) P D P o ( m 1 − 1 ; λ c ) 1 m 1 g k ( z 2 ∣ x 1 ) ∏ i = 1 m 1 f c ( z i ) f c ( z 2 ) p ( θ = 2 , m 1 ∣ z 1 ) p(x_1|\theta=2,z_1)p(\theta=2|z_1)\\=p(x_1|\theta=2,m_1,z_1)p(\theta=2,m_1|z_1)\\=\eta p(x_1|z_0)p(\theta=2,z_1|x_1)p(\theta=2,m_1|z_1)\\=\eta p(x_1|z_0)p(\theta=2,m_1|x_1)p(z_1|x_1,\theta=2,m_1)p(\theta=2,m_1|z_1)\\=\eta p(x_1|z_0)P^DPo(m_1-1;\lambda_c)\frac{1}{m_1}g_k(z^2|x_1)\frac{\prod_{i=1}^{m_1}f_c(z^i)}{f_c(z^2)}p(\theta=2,m_1|z_1) p(x1∣θ=2,z1)p(θ=2∣z1)=p(x1∣θ=2,m1,z1)p(θ=2,m1∣z1)=ηp(x1∣z0)p(θ=2,z1∣x1)p(θ=2,m1∣z1)=ηp(x1∣z0)p(θ=2,m1∣x1)p(z1∣x1,θ=2,m1)p(θ=2,m1∣z1)=ηp(x1∣z0)PDPo(m1−1;λc)m11gk(z2∣x1)fc(z2)∏i=1m1fc(zi)p(θ=2,m1∣z1) It can be seen that , What we have done is to bring in the likelihood probability formula obtained from the previous measurement model , And weight p ( θ = 0 , m 1 ∣ z 1 ) , p ( θ = 1 , m 1 ∣ z 1 ) , p ( θ = 2 , m 1 ∣ z 1 ) p(\theta=0,m_1|z_1),p(\theta=1,m_1|z_1),p(\theta=2,m_1|z_1) p(θ=0,m1∣z1),p(θ=1,m1∣z1),p(θ=2,m1∣z1) These have not been changed and solved . And a priori probability p ( x 1 ∣ z 0 ) p(x_1|z_0) p(x1∣z0) Always exist .
Now we have to face a problem : The weight p ( θ , m 1 ∣ z 1 ) p(\theta,m_1|z_1) p(θ,m1∣z1) How to find ?
Learn from the weight processing of particle filter ( Without detection probability and clutter model )
1. Subjective guess initial value X 0 ∼ N ( μ , σ 2 ) X_0\sim N(\mu,\sigma^2) X0∼N(μ,σ2)
2. according to X 0 ∼ N ( μ , σ 2 ) X_0\sim N(\mu,\sigma^2) X0∼N(μ,σ2) Randomly generate sample points x 0 1 , x 0 2 , . . . , x 0 n x_0^1,x_0^2,...,x_0^n x01,x02,...,x0n
3. Generate X 0 X_0 X0 The weight corresponding to the sample point ω 0 i \omega_0^i ω0i—— It can be all 1 / n 1/n 1/n, It can also be f 0 ( x 0 i ) ∑ f 0 ( x 0 i ) \frac{f_0(x_0^i)}{\sum f_0(x_0^i)} ∑f0(x0i)f0(x0i). among , f 0 ( x ) f_0(x) f0(x) yes X 0 X_0 X0 The probability density function of is N ( μ , σ 2 ) N(\mu,\sigma^2) N(μ,σ2)
4. Generate forecast sample points x 1 i x_1^i x1i: x 1 − i = f m ( x 0 i ) + q 1 x_1^{-i}=f_m(x_0^i)+q_1 x1−i=fm(x0i)+q1 among , q 1 ∼ N ( 0 , Q 1 ) q_1\sim N(0,Q_1) q1∼N(0,Q1) —— It just combines the equation of motion to produce the predicted value .
5. The predicted probability density is obtained according to the predicted sample points : f 1 − ( x ) = ∑ i = 1 n ω 0 i δ ( x − x 1 − i ) f_1^-(x)=\sum_{i=1}^{n}\omega_0^i\delta(x-x_1^{-i}) f1−(x)=i=1∑nω0iδ(x−x1−i) The prediction step just changes the position of the particles, that is x 0 i → x 1 i x_0^i\to x_1^i x0i→x1i, But the weight is not changed ω 0 i \omega_0^i ω0i
6. Observed a data y 1 y_1 y1
7. Bring in the renewal step equation to find the posterior density : f 1 + ( x ) = η f r [ y 1 − h ( x ) ] f 1 − ( x ) = ∑ i = 1 n η f r 1 [ y 1 − h ( x 1 − i ) ] ω 0 i δ ( x − x 1 − i ) = ∑ i = 1 n ω 1 i δ ( x − x 1 − i ) f_1^+(x)=\eta f_r[y_1-h(x)]f_1^-(x)\\=\sum_{i=1}^{n}\eta f_{r1}[y_1-h(x_1^{-i})]\omega_0^i\delta(x-x_1^{-i})\\=\sum_{i=1}^{n}\omega_1^i\delta(x-x_1^{-i}) f1+(x)=ηfr[y1−h(x)]f1−(x)=i=1∑nηfr1[y1−h(x1−i)]ω0iδ(x−x1−i)=i=1∑nω1iδ(x−x1−i) among ω 1 i = η f r [ y 1 − h ( x 1 − i ) ] ω 0 i , f r 1 = N ( 0 , R 1 ) \omega_1^i=\eta f_r[y_1-h(x_1^{-i})]\omega_0^i,f_{r1}=N(0,R_1) ω1i=ηfr[y1−h(x1−i)]ω0i,fr1=N(0,R1), That is, the new step changes the weight value : ω 0 i → ω 1 i \omega_0^i\to\omega_1^i ω0i→ω1i, But the position of the particles has not changed
8. Reunite power ω 1 i = ω 1 i ∑ i = 1 n ω 1 i \omega_1^i=\frac{\omega_1^i}{\sum_{i=1}^{n}\omega_1^i} ω1i=∑i=1nω1iω1i
9. Combine the equation of motion to generate the predicted particles at the next moment x 2 − i = f m ( x 1 − i ) + q 2 x_2^{-i}=f_m(x_1^{-i})+q_2 x2−i=fm(x1−i)+q2 among , q 2 ∼ N ( 0 , Q 2 ) q_2\sim N(0,Q_2) q2∼N(0,Q2)
10. According to the predicted particle points, we can get the predicted probability density f 2 − ( x ) = ∑ i = 1 n ω 1 i δ ( x − x 2 − i ) f_2^-(x)=\sum_{i=1}^{n}\omega_1^i\delta(x-x_2^{-i}) f2−(x)=i=1∑nω1iδ(x−x2−i) The combination of the weight of the previous moment and the particles at this moment —— The prediction step only changes the particle position and the weight remains unchanged
11. Observed a data y 2 y_2 y2
12. Bring in the renewal step equation to find the posterior density : f 2 + ( x ) = η f r [ y 1 − h ( x ) ] f 1 − ( x ) = ∑ i = 1 n η f r 2 [ y 2 − h ( x 2 − i ) ] ω 1 i δ ( x − x 2 − i ) = ∑ i = 1 n ω 2 i δ ( x − x 2 − i ) f_2^+(x)=\eta f_r[y_1-h(x)]f_1^-(x)\\=\sum_{i=1}^{n}\eta f_{r2}[y_2-h(x_2^{-i})]\omega_1^i\delta(x-x_2^{-i})\\=\sum_{i=1}^{n}\omega_2^i\delta(x-x_2^{-i}) f2+(x)=ηfr[y1−h(x)]f1−(x)=i=1∑nηfr2[y2−h(x2−i)]ω1iδ(x−x2−i)=i=1∑nω2iδ(x−x2−i) among ω 2 i = η f r [ y 2 − h ( x 2 − i ) ] ω 1 i , f r 2 = N ( 0 , R 2 ) \omega_2^i=\eta f_r[y_2-h(x_2^{-i})]\omega_1^i,f_{r2}=N(0,R_2) ω2i=ηfr[y2−h(x2−i)]ω1i,fr2=N(0,R2), That is, the new step changes the weight value : ω 1 i → ω 2 i \omega_1^i\to\omega_2^i ω1i→ω2i, But the position of the particles has not changed
13. Weight normalization ω 2 i = ω 2 i ∑ i = 1 n ω 2 i \omega_2^i=\frac{\omega_2^i}{\sum_{i=1}^{n}\omega_2^i} ω2i=∑i=1nω2iω2i
Iterate so constantly …
Be careful : Due to normalization , Actually, the one above η \eta η The coefficient can be omitted directly , namely ω 2 i = f r [ y 2 − h ( x 2 − i ) ] ω 1 i \omega_2^i= f_r[y_2-h(x_2^{-i})]\omega_1^i ω2i=fr[y2−h(x2−i)]ω1i
You can see , The initial weight in particle filter can be set to 1 / n 1/n 1/n, The subsequent change of particle position is based on the equation of motion X k = f m ( X k − 1 ) + q k X_k=f_m(X_{k-1})+q_k Xk=fm(Xk−1)+qk obtain : x k i = f m ( x k − 1 i ) + q k x_k^i=f_m(x_{k-1}^i)+q_k xki=fm(xk−1i)+qk The change of weight is the update step using Bayesian formula ω k i = η f r [ y k − h ( x k − i ) ] ω k − 1 i \omega_k^i=\eta f_r[y_k-h(x_k^{-i})]\omega_{k-1}^i ωki=ηfr[yk−h(xk−i)]ωk−1i
that , S O T SOT SOT Weight in p ( θ , m 1 ∣ z 1 ) p(\theta,m_1|z_1) p(θ,m1∣z1) Is there a similar formula in the update of ?
The formula p ( x k ∣ z 1 : k − 1 ) = ∑ θ 1 : k − 1 ω θ 1 : k − 1 p k ∣ k − 1 θ 1 : k − 1 ( x k ) p ( x k ∣ z 1 : k ) = ∑ θ 1 : k ω θ 1 : k p k ∣ k θ 1 : k ( x k ) p(x_k|z_{1:k-1})=\sum_{\theta_{1:k-1}}\omega^{\theta_{1:k-1}}p_{k|k-1}^{\theta_{1:k-1}}(x_k)\\p(x_k|z_{1:k})=\sum_{\theta_{1:k}}\omega^{\theta_{1:k}}p_{k|k}^{\theta_{1:k}}(x_k) p(xk∣z1:k−1)=θ1:k−1∑ωθ1:k−1pk∣k−1θ1:k−1(xk)p(xk∣z1:k)=θ1:k∑ωθ1:kpk∣kθ1:k(xk) At first glance , Isn't this particle filter ? But take a closer look at , Discovery is the accumulation of all assumptions , Particle filter aims at the accumulation of every sample point , So there is an essential difference between the two , Although very similar in form .
Next is the solution of each term
θ k = 0 \theta_k=0 θk=0 when ω ~ θ 1 : k = ω θ 1 : k ∫ p k ∣ k − 1 θ 1 : k − 1 ( x k ∣ z 1 : k − 1 ) ( 1 − P D ( x k ) ) d x k p k ∣ k θ 1 : k ( x k ∣ z 1 : k ) = η p k ∣ k − 1 θ 1 : k − 1 ( x k ∣ z 1 : k − 1 ) ( 1 − P D ( x k ) ) \tilde{\omega}^{\theta_{1:k}}={\omega}^{\theta_{1:k}}\int p_{k|k-1}^{\theta_{1:k-1}}(x_k|z_{1:k-1})(1-P^D(x_k))dx_k\\p_{k|k}^{\theta_{1:k}}(x_k|z_{1:k})=\eta p_{k|k-1}^{\theta_{1:k-1}}(x_k|z_{1:k-1})(1-P^D(x_k)) ω~θ1:k=ωθ1:k∫pk∣k−1θ1:k−1(xk∣z1:k−1)(1−PD(xk))dxkpk∣kθ1:k(xk∣z1:k)=ηpk∣k−1θ1:k−1(xk∣z1:k−1)(1−PD(xk)) These are what the prediction step and the update step do —— That is, the calculation process of Bayesian filtering
θ k ∈ [ 1 , 2 , 3 , . . . , m ] \theta_k\in [1,2,3,...,m] θk∈[1,2,3,...,m] when ω ~ θ 1 : k = ω θ 1 : k λ ( z θ ) ∫ p k ∣ k − 1 θ 1 : k − 1 ( x k ∣ z 1 : k − 1 ) P D ( x k ) g k ( z k θ k ∣ x k ) d x k p k ∣ k θ 1 : k ( x k ∣ z 1 : k ) = η p k ∣ k − 1 θ 1 : k − 1 ( x k ∣ z 1 : k − 1 ) P D ( x k ) g k ( z k θ k ∣ x k ) \tilde{\omega}^{\theta_{1:k}}=\frac{ {\omega}^{\theta_{1:k}}}{\lambda(z^{\theta})} \int p_{k|k-1}^{\theta_{1:k-1}}(x_k|z_{1:k-1})P^D(x_k)g_k(z_k^{\theta_k}|x_k)dx_k\\p_{k|k}^{\theta_{1:k}}(x_k|z_{1:k})=\eta p_{k|k-1}^{\theta_{1:k-1}}(x_k|z_{1:k-1})P^D(x_k)g_k(z_k^{\theta_k}|x_k) ω~θ1:k=λ(zθ)ωθ1:k∫pk∣k−1θ1:k−1(xk∣z1:k−1)PD(xk)gk(zkθk∣xk)dxkpk∣kθ1:k(xk∣z1:k)=ηpk∣k−1θ1:k−1(xk∣z1:k−1)PD(xk)gk(zkθk∣xk)
Under each assumption, it is a calculation process of bell filter , Then add all the hypothetical calculation results together
It's a little complicated , I feel confused for a while , Let's start with this , I'll add later ( The derivation of this prediction step formula should have )
边栏推荐
- JVM four reference types
- Cause analysis and solution of video jam after easycvr is connected to the device
- AI 改变千行万业,开发者如何投身 AI 语音新“声”态
- Special Lecture 6 tree DP learning experience (long-term update)
- 2、 Uni app login function page Jump
- Mongodb initialization
- 2022年最火的十大测试工具,你掌握了几个
- If you want to change to it, does it really matter if you don't have a major?
- How to solve the problem that easycvr device cannot be online again after offline?
- 6-20漏洞利用-proftpd测试
猜你喜欢
As for the white box test, you have to be skillful in these skills~

配置教程:新版本EasyCVR(v2.5.0)组织结构如何级联到上级平台?

What does real HTAP mean to users and developers?

Three minutes to understand, come to new media

New progress in the implementation of the industry | the openatom openharmony sub forum of the 2022 open atom global open source summit was successfully held
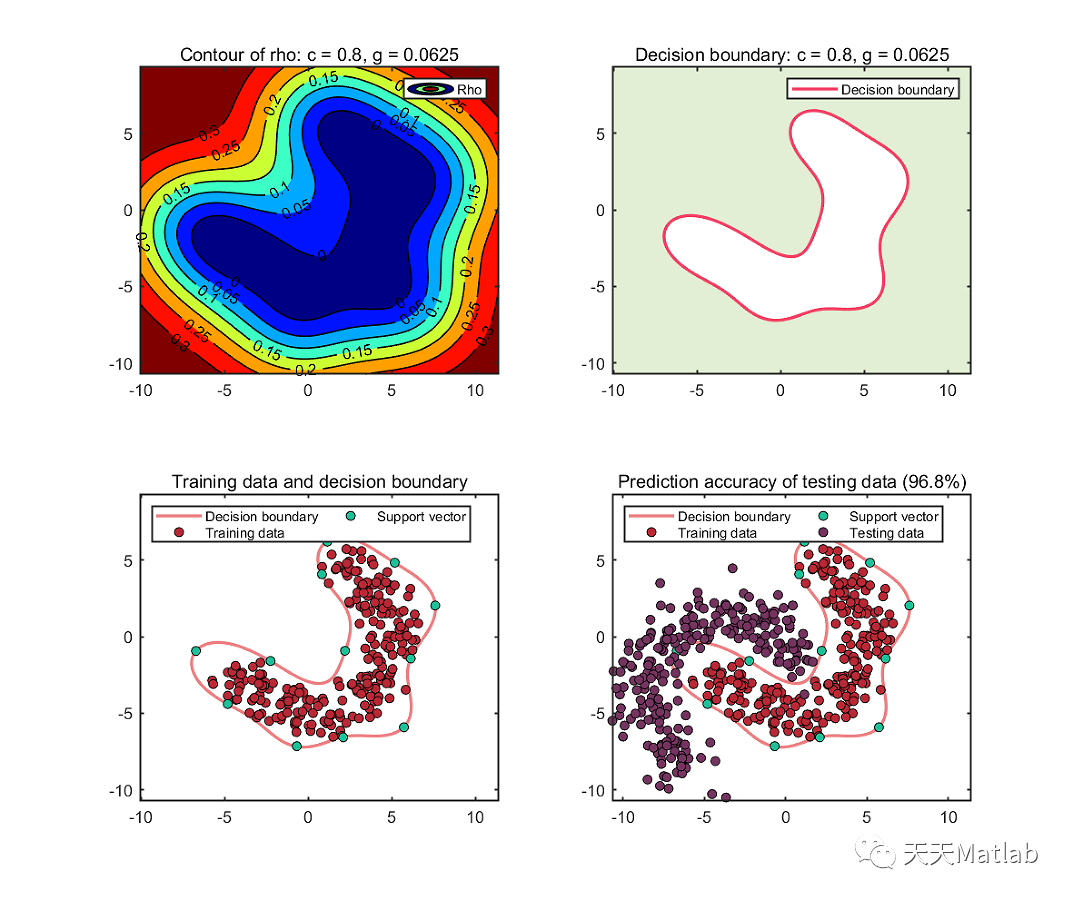
【数据分析】基于MATLAB实现SVDD决策边界可视化

How to use the white list function of the video fusion cloud service easycvr platform?

6-20漏洞利用-proftpd测试

From Bayesian filter to Kalman filter (zero)

BM16 删除有序链表中重复的元素-II
随机推荐
UE4.25 Slate源码解读
4 年后,Debian 终夺回“debian.community”域名!
vim学习手册
【数据分析】基于MATLAB实现SVDD决策边界可视化
What if svchost.exe of win11 system has been downloading?
ECS 5 workflow
Can zero basis software testing work?
真正的 HTAP 对用户和开发者意味着什么?
BM14 链表的奇偶重排
Youqilin system installation beyondcomare
What if the content of software testing is too simple?
Is it useful to learn software testing?
QT function optimization: QT 3D gallery
Software testing dry goods
New upgrade! The 2022 white paper on cloud native architecture was released
Is the software testing industry really saturated?
Is two months of software testing training reliable?
Qt: one signal binds multiple slots
From Bayesian filter to Kalman filter (zero)
优麒麟系统安装BeyondComare