Performance analysis of continuous time system (1) - performance index and first and second order analysis of control system

Self control principle learning notes
Self control principle learning notes column

---

---

Preface

In control theory , The analysis of control system can be divided into time domain analysis and frequency domain analysis . Frequency domain analysis is by inputting sinusoidal input signals of different frequencies to the system , Analyze the steady-state response of the system ; Time domain analysis is to evaluate the performance of the system by studying the time response of the system . This chapter mainly studies the time domain performance and frequency domain performance of the system , Time domain response is to find out the specific response waveform of the system , Frequency analysis can only get the characteristic information of the system response .

1. Control system performance index

1.1 Transient performance

1.1.1 Rise time $t_r$——rise time

Steady state values range from 10%——>90% Time required ; Underdamped ：0_{100%, Overdamping ：10}90%

1.1.2 Peak time $t_p$——peak time

The first peak time when the response reaches the overshoot

1.1.3 Maximum overshoot $M_p$——maximum percent overshoot

Percentage of the final value exceeded for the first time
$$\begin{gathered} M_p=\frac{y(t_p)-y(\infty )}{y(\infty )}\times 100\% \\ \text{Non zero case ：}{M}_p=\frac{y(t_p)-y(\infty )}{y(\infty )-y(0)}\times 100\% \end{gathered}$$
Generally, the faster the response , The greater the overshoot .

1.1.4 Adjust the time $t_s$——settling time

When the steady-state allowable error reaches $2\%\sim 5\%$

1.1.5 Delay time $t_d$——delay time

The response curve reaches $\frac{1}{2}$ The time required for the steady-state value of

1.1.6 Number of oscillations

1.1.7 Attenuation ratio

1.2 Steady state performance

1.2.1 Steady state error ——$e_{ss}$

The error between the actual value and the expected value of the steady-state response of the steady-state system .

2. Typical first-order time domain analysis

2.1 Definition

The typical first-order system block diagram can be simplified as follows .

structure characteristics ：

1. Unit negative feedback
2. Open loop transfer function is another integral link , The open-loop gain is the reciprocal of the time constant $K=\frac{1}{T}$

2.2 Response of typical links

1. Unit step response -$r(t)=ϵ(t),R(s)=\frac{1}{s}$

   Output is ：
   $$\begin{gathered} y(t)=1-{\mathrm{e}}^{-\frac{t}{T}}\to 1 \\ {e}_{ss}=\underset{t\to \infty }{\lim }e(t)=0 \end{gathered}$$
   The steady-state error is ：

2. Unit impulse response -$r(t)=\delta (t),R(s)=1$

   Output is ：
   $$y(t)=\frac{1}{T}{\mathrm{e}}^{-t/T}\to 0$$
   The steady-state error is ：
   $$\begin{gathered} e(t)=r(t)-y(t)=\delta (t)-T{e}^{-\frac{1}{T}t} \\ {e}_{ss}=\underset{t\to \infty }{\lim }e(t)=\delta (t)-T \end{gathered}$$

3. Unit slope response -$r(t)=t,R(s)=\frac{1}{s^2}$

   Output is ：
   $$y(t)=t-T+T{\mathrm{e}}^{-t/T}\to t-T$$
   Steady state error ：
   $$\begin{gathered} e(t)=r(t)-y(t)=T(1-e^{-\frac{1}{T}t}) \\ {e}_{ss}=\underset{t\to \infty }{\lim }e(t)=T \end{gathered}$$

4. Unit acceleration response -$r(t)=\frac{1}{2}{t}^2,R(s)=\frac{1}{s^3}$

   Output is ：
   $$y(t)=\frac{1}{2}{t}^2-Tt+T^2\left(1-{\mathrm{e}}^{-\frac{1}{T}t}\right)\to \frac{1}{2}{t}^2-Tt+T^2$$
   Steady state error ：
   $$\begin{gathered} e(t)=r(t)-y(t)=Tt-T^2(1-e^{-\frac{1}{T}t}) \\ {e}_{ss}=\underset{t\to \infty }{\lim }e(t)=\infty \end{gathered}$$
   The following figure shows the unit impulse response , Unit step response , Response function of unit slope response , You can see that the unit responds to each link by presenting integral / Differential relation , Then their output has also been integrated / Differential link .

3. Typical second-order time domain analysis

3.1 Definition

1. Transfer function ：
   $$\frac{Y(s)}{R(s)}=\frac{{\omega }_{\mathrm{n}}^2}{s^2+2\zeta {\omega }_{\mathrm{n}}s+{\omega }_{\mathrm{n}}^2}$$

2. Typical structure diagram ：
   

3. Structural features :

   (1) Unit negative feedback structure

   (2) The open-loop transfer function has only one integral link , The open-loop gain is $K=w_n/(2\zeta )$

3.2 Response of typical links

1. Slope response

   Output is :
   $$Y(s)=\frac{1}{s^2}\cdot \frac{{\omega }_{\mathrm{n}}^2}{s^2+2\zeta {\omega }_{\mathrm{n}}s+{\omega }_{\mathrm{n}}^2}$$
   Steady state error :
   $$\begin{array}{rl}E(s)& =R(s)-Y(s)=\frac{1}{s^2}-\frac{1}{s^2}\cdot \frac{{\omega }_{\mathrm{n}}^2}{s^2+2\zeta {\omega }_{\mathrm{n}}s+{\omega }_{\mathrm{n}}^2}\\ & =\frac{1}{s}\cdot \frac{s+2\zeta {\omega }_{\mathrm{n}}}{s^2+2\zeta {\omega }_{\mathrm{n}}s+{\omega }_{\mathrm{n}}^2}\\ e_{ss}=\underset{t\to \infty }{\lim }e(t)& =\underset{s\to 0}{\lim }sE(s)=\underset{s\to 0}{\lim }\frac{s+2\zeta {\omega }_{\mathrm{n}}}{s^2+2\zeta {\omega }_{\mathrm{n}}s+{\omega }_{\mathrm{n}}^2}=\frac{2\zeta }{{\omega }_{\mathrm{n}}}\end{array}$$

2. The relationship between transient performance and damping coefficient and natural frequency angular frequency

   $\zeta >1$: Overdamping

   $\zeta =1$: Critical damping

   $0<\zeta <1$: Underdamped , It has good transient performance , Attenuated oscillation .

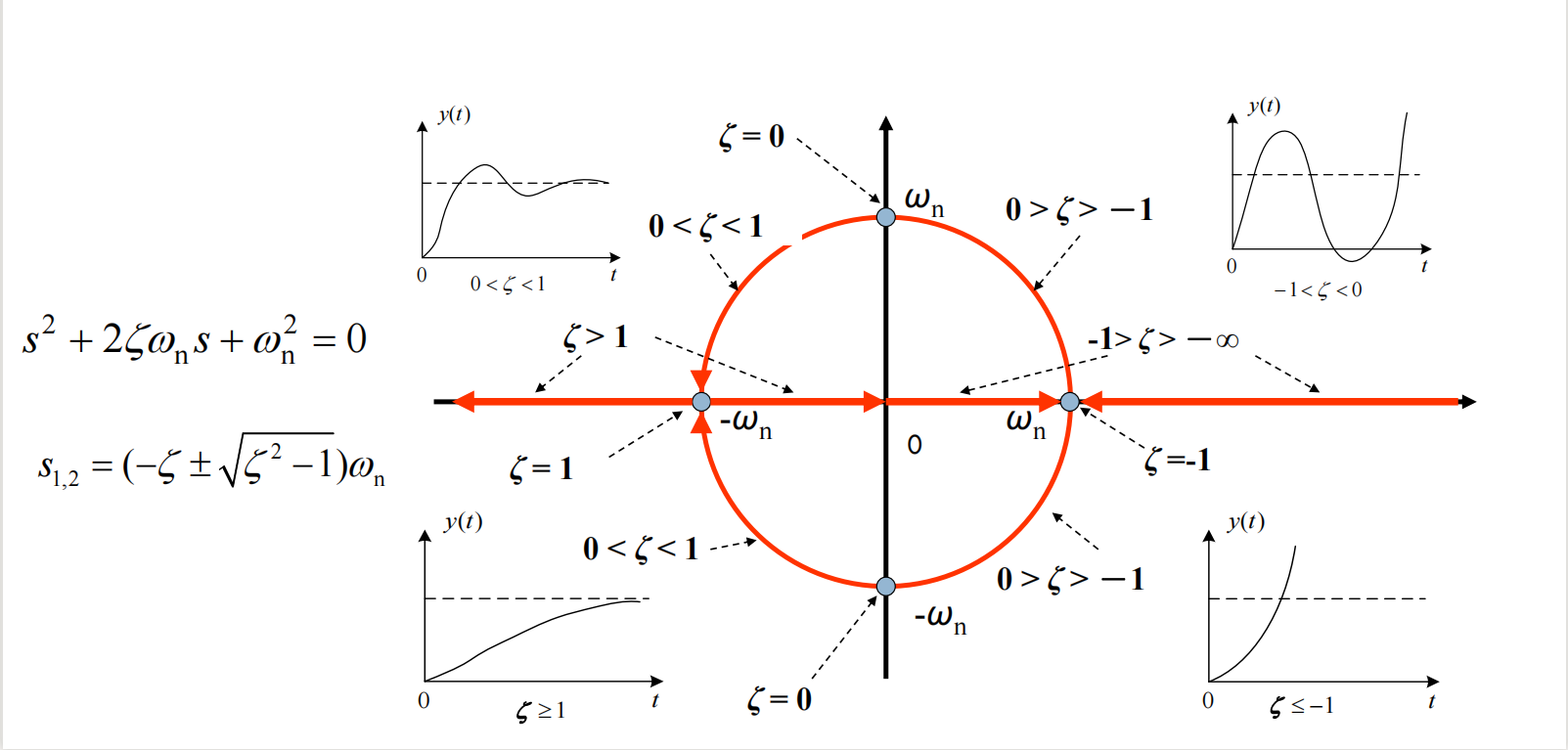
4. Underdamped transient performance

4.1 Take the unit step response as an example :

$$\begin{array}{rl}Y(s)=& \frac{1}{s}\cdot \frac{{\omega }_{\mathrm{n}}^2}{s^2+2\zeta {\omega }_{\mathrm{n}}s+{\omega }_{\mathrm{n}}^2}\\ =& \frac{1}{s}-\frac{s+\zeta {\omega }_{\mathrm{n}}}{{\left(s+\zeta {\omega }_{\mathrm{n}}\right)}^2+\left(1-{\zeta }^2\right){\omega }_{\mathrm{n}}^2}-\frac{\zeta }{{\left(s+\zeta {\omega }_{\mathrm{n}}\right)}^2+\left(1-{\zeta }^2\right){\omega }_{\mathrm{n}}^2}\end{array}$$

$$\begin{array}{rl}y(t)& =1-{\mathrm{e}}^{-\zeta {\omega }_{\mathrm{n}}t}\left[\cos \left(\sqrt{1-{\zeta }^2}{\omega }_{\mathrm{n}}t\right)+\frac{\zeta }{\sqrt{1-{\zeta }^2}}\sin \left(\sqrt{1-{\zeta }^2}{\omega }_{\mathrm{n}}t\right)\right]\\ & =1-\frac{{\mathrm{e}}^{-\zeta {\omega }_{\mathrm{n}}t}}{\sqrt{1-{\zeta }^2}}\left[\sqrt{1-{\zeta }^2}\cos \left(\sqrt{1-{\zeta }^2}{\omega }_{\mathrm{n}}t\right)+\zeta \sin \left(\sqrt{1-{\zeta }^2}{\omega }_{\mathrm{n}}t\right)\right]\\ & =1-\frac{{\mathrm{e}}^{-\zeta {\omega }_{\mathrm{n}}t}}{\sqrt{1-{\zeta }^2}}[\sin (\arccos \zeta )\cos \left(\sqrt{1-{\zeta }^2}{\omega }_{\mathrm{n}}t\right)+\cos (\arccos \zeta )\sin (\sqrt{1-{\zeta }^2{\omega }_{\mathrm{n}}t}\\ & =1-\frac{{\mathrm{e}}^{-\zeta {\omega }_{\mathrm{n}}t}}{\sqrt{1-{\zeta }^2}}\sin \left(\sqrt{1-{\zeta }^2}{\omega }_{\mathrm{n}}t+\arccos \zeta \right)\end{array}$$

$rememberfailurereducesystemCount\sigma =\zeta w_n,ResistanceNiVibrationSwingfrequencyrate{w}_d=\sqrt{1-{\zeta }^2}{w}_n,\cos \beta =\zeta ,\sin \beta =\sqrt{1-{\zeta }^2},Itsin\beta callbyResistanceNihorn$

4.2 Transient performance index

1. Peak time
   $$\begin{array}{rl}Make\dot{y}(t)& =0,namely\\ & \frac{{\mathrm{e}}^{-\sigma t}{\omega }_{\mathrm{n}}}{\sqrt{1-{\zeta }^2}}\sin \left({\omega }_{\mathrm{d}}t\right)=0\\ have\; toTo:& \\ & t=\frac{k\pi }{{\omega }_d},k=1,2,\cdots \\ The\; firstOneindividualpeakvalueOfwhenbetweenby& \\ t_{\mathrm{p}}& =\frac{\pi }{{\omega }_{\mathrm{d}}}=\frac{\pi }{{\omega }_{\mathrm{n}}\sqrt{1-{\zeta }^2}}\end{array}$$

2. Maximum overshoot

   Calculate the peak time by substituting it into the definition
   $$M_p=e^{-\frac{\pi \zeta }{\sqrt{1-{\zeta }^2}}}\times 100\%$$

3. Adjust the time (5%)

   Envelope curve is often used to replace actual curve estimation in engineering , Make $\frac{e^{-\zeta w_{n}t}}{\sqrt{1-{\zeta }^2}}=0.05$
   $$\begin{gathered} t_{\mathrm{s}}=-\frac{\ln \left(0.05\sqrt{1-{\zeta }^2}\right)}{\zeta {\omega }_{\mathrm{n}}} \\ When0<\zeta <0.8when,nearlikeYes \\ {t}_{\mathrm{s}}=\frac{3\sim 3.5}{\zeta {\omega }_{\mathrm{n}}} \end{gathered}$$

4. Rise time
   $$t_{\mathrm{r}}=\frac{\pi -\beta }{{\omega }_{\mathrm{d}}}=\frac{\pi -\beta }{{\omega }_{\mathrm{n}}\sqrt{1-{\zeta }^2}}$$

$Makey(t)=1-\frac{e^{-\sigma t}}{\sqrt{1-{\zeta }^2}}\sin \left({\omega }_{\mathrm{d}}t+\beta \right)=1,JustcanWithhave\; toTo{t}_{\mathrm{r}}=\frac{\pi -\beta }{{\omega }_{\mathrm{d}}}.$

4.3 summary

1. $\zeta$ The smaller it is , The greater the overshoot , The less stable , The longer the adjustment time
2. $\zeta$ Too big , The system is slow to respond , The adjustment time is also long , Poor rapidity
3. Usually take $\zeta$ by 0.707