Performance analysis of continuous time systems (2) - second order system performance improvement methods PID, PR

Self control principle learning notes
Self control principle learning notes column

---

---

4. Second order system performance improvement

4.1 P-Proportion

4.1.1 Open loop transfer function ：

$$L(s)=\frac{K_p{w}_n^2}{s(s+2\zeta w_n)}$$

4.1.2 Closed loop transfer function of the system ：

$$\Phi (s)=\frac{Y(s)}{R(s)}=\frac{K_p{w}_n^2}{s^2+2\zeta w_{n}s+K_p{w}_n^2}=\frac{w_{np}^2}{s^2+2{\zeta }_p{w}_{np}s+w_{np}^2}$$

4.1.3 Compare typical links

1. The real part of the characteristic root remains unchanged

2. Closed loop gain $\Phi (s){|}_{s=0}=1$ Don't change ; Open loop speed gain $K=s^{1}L(s){|}_{s=0}=\frac{K_p{w}_n}{2\zeta }$

3. Natural frequency $w_{np}=\sqrt{K_p}{w}_n$

4. Damping coefficient ${\zeta }_p=\zeta /\sqrt{K_p}$

5. The adjustment time is basically unchanged

4.2 PD-Proportion Derivate

4.2.1 Open loop transfer function

$$L(s)=\frac{(T_{d}s+1)w_n^2}{s\left(s+2\zeta w_n\right)}$$

4.2.2 Closed loop transfer function

$$\Phi (s)=\frac{Y(s)}{R(s)}=\frac{w_n^2(T_{d}s+1)}{s^2+2\zeta w_{n}s+w_n^2{T}_{d}s+w_n^2}=\frac{w_n^2(T_{d}s+1)}{s^2+2{\zeta }_d{w}_{n}s+w_n^2}$$

4.2.3 Compare typical links

1. The closed-loop gain is 1, The open-loop gain is $K=\frac{w_n}{2\zeta }$

2. Natural frequencies do not change , The damping coefficient increases , Overshoot becomes smaller ——${\zeta }_d=\zeta +\frac{T_d{w}_n}{2}$

3. The step response of the system is equivalent to adding an impulse response , The range is $T_d$ times , Speed up the dynamic response of the system
   $$Y(s)=\frac{w_n^2}{s^2+2{\zeta }_d{w}_{n}s+w_n^2}\ast \frac{1}{s}+\frac{w_n^2\cdot T_d}{s^2+2{\zeta }_d{w}_{n}s+w_n^2}$$

4.2.4 Qualitative conclusion

1. Increase the system resistance ratio , It does not affect the natural frequency of the system , So as to suppress the oscillation , Reduce overshoot , Improve system stability .
2. Zero appears , Speed up the response of the system
3. Differential has amplification effect on high-frequency noise , When the input noise is high , Do not use

4.3 PI-Proportion Integral

4.3.1 Open loop transfer function

$$L(s)=\frac{(T_{i}s+1)w_n^2}{T_i{s}^2\left(s+2\zeta w_n\right)}$$

4.3.2 Closed loop transfer function

$$\begin{gathered} \frac{Y(s)}{R(s)}=\frac{{\omega }_{\mathrm{n}}^2\left(T_{\mathrm{i}}s+1\right)}{T_{\mathrm{i}}{s}^3+2T_{\mathrm{i}}\zeta {\omega }_{\mathrm{n}}{s}^2+T_{\mathrm{i}}{\omega }_{\mathrm{n}}{}^{2}s+{\omega }_{\mathrm{n}}^2} \\ \frac{Y(s)}{D(s)}=\frac{{\omega }_{\mathrm{n}}^2{T}_{\mathrm{i}}s}{T_{\mathrm{i}}{s}^3+2T_{\mathrm{i}}\zeta {\omega }_{\mathrm{n}}{s}^2+T_{\mathrm{i}}{\omega }_{\mathrm{n}}{}^{2}s+{\omega }_{\mathrm{n}}^2} \end{gathered}$$

4.3.3 Compare typical links

1. Given the closed-loop position gain to the output is 1
2. The open-loop acceleration gain is $K=s^{2}L(s){|}_{s=0}=\frac{w_n}{2\zeta T_i}$
3. The static gain of disturbance to output transfer function is 0
4. The order of the system is determined by 1 Step becomes 2 rank

4.3.4 Qualitative conclusion

1. The order of the system rises , Improper selection of parameters may cause RHP pole
2. Introduce the integral link , Eliminate the error caused by constant value disturbance
3. The integration link reduces the response speed , The overshoot may be increased at the initial stage of response

4.4 PID-Proportion Integral Derivate

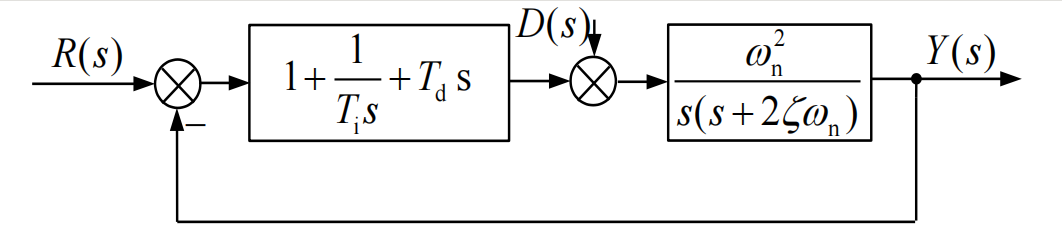
4.4.1 Open loop transfer function

$$L(s)=\frac{(T_i{T}_d{s}^2+T_{i}s1)w_n^2}{T_i{s}^2\left(s+2\zeta w_n\right)}$$

4.4.2 Closed loop transfer function

$$\begin{gathered} \frac{Y(s)}{R(s)}=\frac{T_{\mathrm{d}}{T}_{\mathrm{i}}{\omega }_{\mathrm{n}}^2{s}^2+T_{\mathrm{i}}{\omega }_{\mathrm{n}}^{2}s+{\omega }_{\mathrm{n}}^2}{T_{\mathrm{i}}{s}^3+\left(2T_{\mathrm{i}}\zeta {\omega }_{\mathrm{n}}+T_{\mathrm{d}}{T}_{\mathrm{i}}{\omega }_{\mathrm{n}}^2\right)s^2+T_{\mathrm{i}}{\omega }_{\mathrm{n}}^{2}s+{\omega }_{\mathrm{n}}^2} \\ \frac{Y(s)}{D(s)}=\frac{{\omega }_{\mathrm{n}}^2{T}_{\mathrm{i}}s}{T_{\mathrm{i}}{s}^3+\left(2T_{\mathrm{i}}\zeta {\omega }_{\mathrm{n}}+T_{\mathrm{d}}{T}_{\mathrm{i}}{\omega }_{\mathrm{n}}^2\right)s^2+T_{\mathrm{i}}{\omega }_{\mathrm{n}}^{2}s+{\omega }_{\mathrm{n}}^2} \end{gathered}$$

4.4.3 Compare typical links

1. Given the closed-loop position gain to the output is 1
2. The open-loop acceleration gain is $K=s^{2}L(s){|}_{s=0}=\frac{w_n}{2\zeta T_i}$
3. The static gain of disturbance to output transfer function is 0
4. The order of the system is determined by 1 Step becomes 2 rank

4.4.4 Qualitative conclusion

1. P—— Improve response speed ;I—— Eliminate steady-state errors ;D—— Appropriately speed up the transient response , Suppress overshoot
2. Eliminate the error caused by constant value disturbance .

4.5 Differential feedback

4.5.1 Open loop transfer function ：

$$L(s)=\frac{{\omega }_{\mathrm{n}}^2}{s\left(2\zeta {\omega }_{\mathrm{n}}+k{\omega }_{\mathrm{n}}{}^2\right)}$$

4.5.2 Closed loop transfer function ：

$$\frac{Y(s)}{R(s)}=\frac{{\omega }_{\mathrm{n}}^2}{s^2+\left(2\zeta {\omega }_{\mathrm{n}}+k{\omega }_{\mathrm{n}}{}^2\right)s+{\omega }_{\mathrm{n}}^2}$$

4.5.3 Compare typical links

1. The closed-loop position gain is 1
2. The open-loop speed gain is reduced to $K=\frac{w_n^2}{2\zeta w_n+k{w}_n^2}$
3. The natural frequency remains unchanged
4. The damping coefficient increases ${\zeta }_{df}=\zeta +\frac{1}{2}k{w}_n$

4.4.5 Qualitative conclusion

1. Does not affect natural frequency , Increase the damping ratio of the system , Reduce overshoot
2. Reduce the open-loop gain , Increase the steady-state error of system slope input
3. No closed-loop zero , The output stability is better than PD Adjust the