当前位置:网站首页>漫画:如何实现大整数相乘?(下)
漫画:如何实现大整数相乘?(下)
2022-07-05 16:51:00 【小灰】
如何用程序实现大整数相乘呢?
在上一篇文章 漫画:如何实现大整数相乘?(上) 修订版 当中,我们介绍了两种思路:
1.像列竖式一样,把两整数按位依次相乘
这个思路的时间复杂度是O(n^2)。
2.利用分治法,把每个大整数分成高位和低位两部分,转化成四个较小的乘积。
这个思路的时间复杂度同样是O(n^2)。
那么,有什么样的优化方案,可以使时间复杂度优于O(n^2)呢?我们今天一起来研究下。
如何做调整呢?其实很简单,连小学生都会:
这样一来,原本的4次乘法和3次加法,转变成了3次乘法和6次加法。
这样一来,时间复杂度是多少呢?
假设两个长度为n的大整数相乘,整体运算规模是T(n) 。
刚才我们说过,两个大整数相乘可以被拆分成三个较小的乘积,
所以在第一次分治时,T(n)和T(n/2)有如下关系:
T(n) = 3T(n/2) + f(n)
其中f(n)是6次加法的运算规模,f(n)的渐进时间复杂度很明显是O(n)。
此时让我们回顾一下master定理:
设常数a >= 1,b > 1,如果一个算法的整体计算规模 T(n) = a T(n / b) + f(n),那么则有如下规律:
对于T(n) = 3T(n/2) + f(n)这个关系式来说, a=3, b=2。
把a和b的值,以及f(n)的时间复杂度带入到master定理的第一个规律,也就是下面的规律:
发现正好符合条件。
怎么符合条件呢?推导过程如下:
所以我们的平均时间复杂度是:
2 和 1.59 之间的差距看似不大,但是当整数长度非常大的时候,两种方法的性能将是天壤之别。
下面展示一下实现代码。我们的代码非常复杂,在这里只作为参考,最重要的还是解决问题的思路:
/**
* 大整数乘法
* @param bigNumberA 大整数A
* @param bigNumberB 大整数B
*/
public static String bigNumberMultiply(String bigNumberA, String bigNumberB) {
boolean isNegative = false;
if ((bigNumberA.startsWith("-") && bigNumberB.startsWith("-"))
|| (!bigNumberA.startsWith("-") && !bigNumberB.startsWith("-"))) {
// 两数同符号的情况
bigNumberA = bigNumberA.replaceAll("-", "");
bigNumberB = bigNumberB.replaceAll("-", "");
} else if ((bigNumberA.startsWith("-") && !bigNumberB.startsWith("-"))
|| (!bigNumberA.startsWith("-") && bigNumberB.startsWith("-"))) {
// 两数不同符号的情况
bigNumberA = bigNumberA.replace("-", "");
bigNumberB = bigNumberB.replace("-", "");
isNegative = true;
}
// 如果两数长度之和小于10,直接相乘返回
if (bigNumberA.length() + bigNumberB.length() < 10) {
// 计算乘积
int tmp = (Integer.parseInt(bigNumberA) * Integer.parseInt(bigNumberB));
if (tmp == 0) {
return "0";
}
String value = String.valueOf(tmp);
if(isNegative){
value = "-" + value;
}
return value;
}
// 公式 AC * 10^n+((A-B)(D-C)+AC+BD) * 10^(n/2)+BD当中的a,b,c,d
String a, b, c, d;
if (bigNumberA.length() == 1) {
a = "0";
b = bigNumberA;
} else {
if (bigNumberA.length() % 2 != 0) {
bigNumberA = "0" + bigNumberA;
}
a = bigNumberA.substring(0, bigNumberA.length() / 2);
b = bigNumberA.substring(bigNumberA.length() / 2);
}
if (bigNumberB.length() == 1) {
c = "0";
d = bigNumberB;
} else {
if (bigNumberB.length() % 2 != 0) {
bigNumberB = "0" + bigNumberB;
}
c = bigNumberB.substring(0, bigNumberB.length() / 2);
d = bigNumberB.substring(bigNumberB.length() / 2);
}
// 按最大位数取值,以确定补零数目
int n = bigNumberA.length() >= bigNumberB.length() ? bigNumberA.length() : bigNumberB.length();
//t1,t2为中间运算结果,t3为乘法运算完毕的结果
String t1, t2, t3;
String ac = bigNumberMultiply(a, c);
String bd = bigNumberMultiply(b, d);
//t1=(A-B)(D-C)
t1 = bigNumberMultiply(bigNumberSubtract(a, b), bigNumberSubtract(d, c));
//t2=(A-B)(D-C)+AC+BD
t2 = bigNumberSum(bigNumberSum(t1, ac), bd);
//t3= AC * 10^n+((A-B)(D-C)+AC+BD) * 10^(n/2)+BD
t3 = bigNumberSum(bigNumberSum(Power10(ac, n), Power10(t2, n/2)), bd).replaceAll("^0+", "");
if (t3 == "")
return "0";
if(isNegative){
return "-" + t3;
}
return t3;
}
/**
* 大整数加法
* @param bigNumberA 大整数A
* @param bigNumberB 大整数B
*/
public static String bigNumberSum(String bigNumberA, String bigNumberB) {
if (bigNumberA.startsWith("-") && !bigNumberB.startsWith("-")) {
return bigNumberSubtract(bigNumberB, bigNumberA.replaceAll("^-", ""));
} else if (!bigNumberA.startsWith("-") && bigNumberB.startsWith("-")) {
return bigNumberSubtract(bigNumberA, bigNumberB.replaceAll("^-", ""));
} else if (bigNumberA.startsWith("-") && bigNumberB.startsWith("-")) {
return "-" + bigNumberSum(bigNumberA.replaceAll("^-", ""), bigNumberB.replaceAll("^-", ""));
}
//1.把两个大整数用数组逆序存储,数组长度等于较大整数位数+1
int maxLength = bigNumberA.length() > bigNumberB.length() ? bigNumberA.length() : bigNumberB.length();
int[] arrayA = new int[maxLength+1];
for(int i=0; i< bigNumberA.length(); i++){
arrayA[i] = bigNumberA.charAt(bigNumberA.length()-1-i) - '0';
}
int[] arrayB = new int[maxLength+1];
for(int i=0; i< bigNumberB.length(); i++){
arrayB[i] = bigNumberB.charAt(bigNumberB.length()-1-i) - '0';
}
//2.构建result数组,数组长度等于较大整数位数+1
int[] result = new int[maxLength+1];
//3.遍历数组,按位相加
for(int i=0; i<result.length; i++){
int temp = result[i];
temp += arrayA[i];
temp += arrayB[i];
//判断是否进位
if(temp >= 10){
temp -= 10;
result[i+1] = 1;
}
result[i] = temp;
}
//4.把result数组再次逆序并转成String
StringBuilder sb = new StringBuilder();
//是否找到大整数的最高有效位
boolean findFirst = false;
for (int i = result.length - 1; i >= 0; i--) {
if(!findFirst){
if(result[i] == 0){
continue;
}
findFirst = true;
}
sb.append(result[i]);
}
return sb.toString();
}
/**
* 大整数减法
* @param bigNumberA 大整数A
* @param bigNumberB 大整数B
*/
public static String bigNumberSubtract(String bigNumberA, String bigNumberB) {
int compareResult = compare(bigNumberA, bigNumberB);
if (compareResult == 0) {
return "0";
}
boolean isNegative = false;
if (compareResult == -1) {
String tmp = bigNumberB;
bigNumberB = bigNumberA;
bigNumberA = tmp;
isNegative = true;
}
//1.把两个大整数用数组逆序存储,数组长度等于较大整数位数+1
int maxLength = bigNumberA.length() > bigNumberB.length() ? bigNumberA.length() : bigNumberB.length();
int[] arrayA = new int[maxLength+1];
for(int i=0; i< bigNumberA.length(); i++){
arrayA[i] = bigNumberA.charAt(bigNumberA.length()-1-i) - '0';
}
int[] arrayB = new int[maxLength+1];
for(int i=0; i< bigNumberB.length(); i++){
arrayB[i] = bigNumberB.charAt(bigNumberB.length()-1-i) - '0';
}
//2.构建result数组,数组长度等于较大整数位数+1
int[] result = new int[maxLength+1];
//3.遍历数组,按位相加
for(int i=0; i<result.length; i++){
int temp = result[i];
temp += arrayA[i];
temp -= arrayB[i];
//判断是否进位
if(temp < 0){
temp += 10;
result[i+1] = -1;
}
result[i] = temp;
}
//4.把result数组再次逆序并转成String
StringBuilder sb = new StringBuilder();
//是否找到大整数的最高有效位
boolean findFirst = false;
for (int i = result.length - 1; i >= 0; i--) {
if(!findFirst){
if(result[i] == 0){
continue;
}
findFirst = true;
}
sb.append(result[i]);
}
String value = sb.toString();
if (isNegative) {
value = "-" + value;
}
return value;
}
// 比较大小
private static int compare(String x, String y) {
if (x.length() > y.length()) {
return 1;
} else if (x.length() < y.length()) {
return -1;
} else {
for (int i = 0; i < x.length(); i++) {
if (x.charAt(i) > y.charAt(i)) {
return 1;
} else if (x.charAt(i) < y.charAt(i)) {
return -1;
}
}
return 0;
}
}
// 扩大10的n次方倍
public static String Power10(String num, int n) {
for (int i = 0; i < n; i++) {
num += "0";
}
return num;
}
public static void main(String[] args) {
String x = "1513143";
String y = "9345963";
System.out.println(bigNumberMultiply(x, y));
}需要注意的是,这段实现代码只适用于两个大整数长度相等的情况。如果想求解长度不等的整数相乘,只需要对代码做微小的改动,有兴趣的小伙伴没有试一试。
几点补充:
1. 文章最后的代码,经由网上技术博客的代码改动而来,仅做参考。
2. 关于快速傅里叶变换,有兴趣深入研究的小伙伴们可以参考《算法导论》第30章的内容。
—————END—————
边栏推荐
- 2022 年 Q2 加密市场投融资报告:GameFi 成为投资关键词
- Embedded -arm (bare board development) -1
- Cloud security daily 220705: the red hat PHP interpreter has found a vulnerability of executing arbitrary code, which needs to be upgraded as soon as possible
- 网上办理期货开户安全吗?网上会不会骗子比较多?感觉不太靠谱?
- 域名解析,反向域名解析nbtstat
- [Jianzhi offer] 61 Shunzi in playing cards
- 【剑指 Offer】62. 圆圈中最后剩下的数字
- 云安全日报220705:红帽PHP解释器发现执行任意代码漏洞,需要尽快升级
- C how TCP restricts the access traffic of a single client
- MySQL queries the latest qualified data rows
猜你喜欢
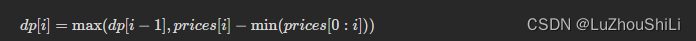
【剑指 Offer】63. 股票的最大利润

激动人心!2022开放原子全球开源峰会报名火热开启!
Oracle缩表空间的完整解决实例
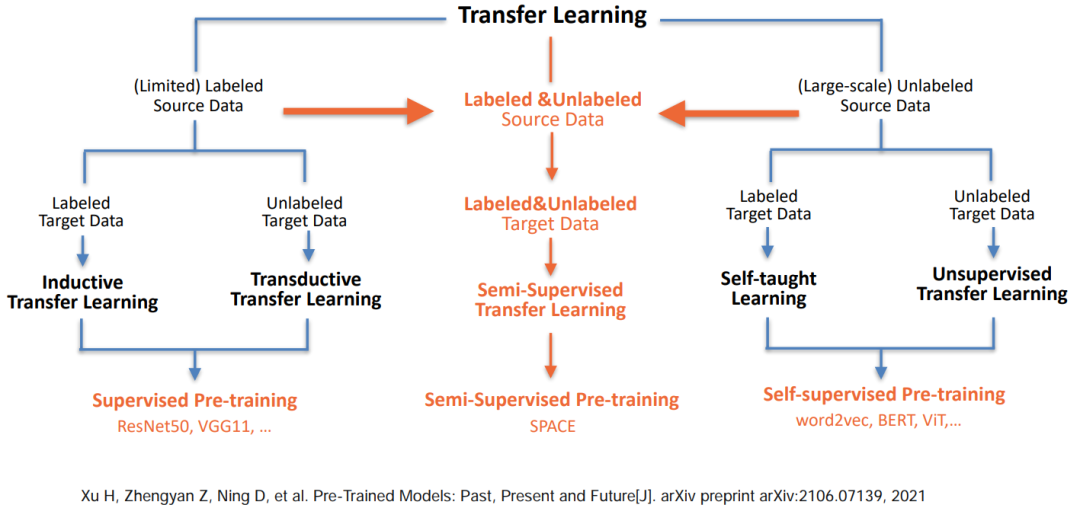
干货!半监督预训练对话模型 SPACE
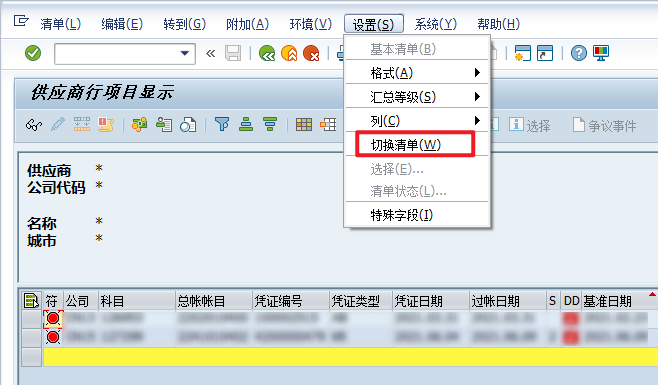
VBA驱动SAP GUI实现办公自动化(二):判断元素是否存在

The survey shows that the failure rate of traditional data security tools in the face of blackmail software attacks is as high as 60%

【性能测试】jmeter+Grafana+influxdb部署实战
一文了解MySQL事务隔离级别
In depth understanding of redis memory obsolescence strategy

The second day of learning C language for Asian people
随机推荐
Q2 encryption market investment and financing report in 2022: gamefi becomes an investment keyword
Etcd build a highly available etcd cluster
thinkphp3.2.3
[Jianzhi offer] 61 Shunzi in playing cards
Embedded -arm (bare board development) -2
winedt常用快捷键 修改快捷键latex编译按钮
Embedded -arm (bare board development) -1
华为云云原生容器综合竞争力,中国第一!
一文了解MySQL事务隔离级别
Machine learning compilation lesson 2: tensor program abstraction
一个满分的项目文档是如何书写的|得物技术
【剑指 Offer】63. 股票的最大利润
张平安:加快云上数字创新,共建产业智慧生态
【性能测试】jmeter+Grafana+influxdb部署实战
Little knowledge about C language (array and string)
Use byte stream to read Chinese from file to console display
激动人心!2022开放原子全球开源峰会报名火热开启!
[wechat applet] read the life cycle and route jump of the applet
Is it safe to open futures accounts online? Will there be more liars online? Doesn't feel very reliable?
Redis+caffeine two-level cache enables smooth access speed