Machine learning -- detailed introduction of standardscaler (), transform (), fit () in sklearn package

• sklearn（scikit-learn） yes Scipy An extension of , Based on the NumPy and matplotlib Library based . since 2007 Since its release ,sklearn Has become a Python Important machine learning library .
• sklearn Support includes classification 、 Return to 、 The four big machine learning algorithms of descending and clustering . It also includes feature extraction 、 Data processing and model evaluation .

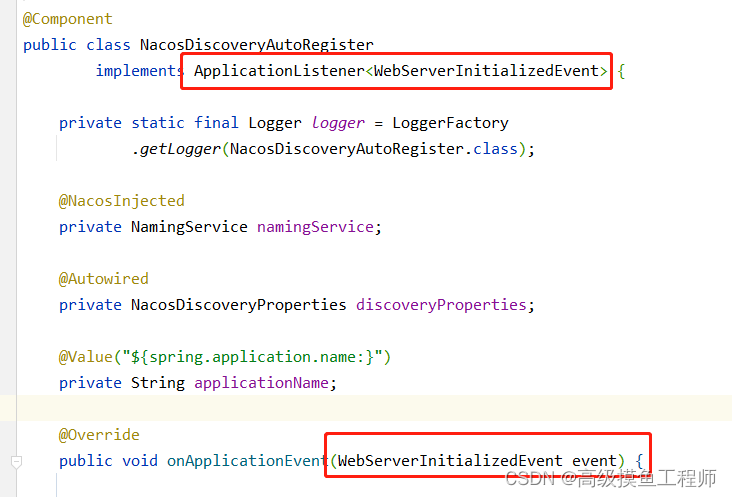
One 、 Sklearn In bag StandardScaler()

        1. from sklearn.preprocessing import StandardScaler  # Import standardized functions in the data processing module

        2. SS = StandardScaler()         # Generate entity class module

        3. scaler=SS.fit(X_train)        # In essence, it is to find the mean and variance of each column

        4. X_train=scaler.transform(X_train)     # Standardize the data columns

        5.# Use the mean and variance of each column in the training set to standardize each column in the test set .
        test1=scaler.transform(X_test1)
        test2=scaler.transform(X_test2)

  Two 、 Method 2 （ Data standardization )：

mean=train_data.mean(axis=0)
train_data-=mean
std=train_data.std(axis=0)
train_data/=std
test_data-=mean
test_data/=std

Be careful , The mean and standard deviation used for the standardization of test data are calculated on the training data . In the workflow , You can't calculate any results on the test data , Even simple things like data standardization are not allowed .