Opencv:08 image pyramid

Image pyramid

Introduction to image pyramid

Image pyramid It is a kind of multi-scale expression in image , It is mainly used for image segmentation , It is an effective and simple structure to interpret images with multi-resolution . Simply speaking , Image pyramid is a collection of subgraphs with different resolutions of the same image （ Yes 800×800、480×640…）

Image pyramids were originally used for Machine vision and Image compression , The pyramid of an image is a series arranged in the shape of a pyramid The resolution gradually decreases 、 And From the same original picture Of Image set . It is obtained by step down sampling , Stop sampling until a certain termination condition is reached .

At the bottom of the pyramid is a high-resolution representation of the image to be processed , And at the top is a low resolution approximation . We compare layers of images to pyramids , The higher the level , The smaller the image , Lower resolution

The Gaussian pyramid fixes the zoom ratio , That is, if you are 800×800 Graph , Cannot zoom to 500×500

We are going to learn how to use , How to generate these image pyramids

---

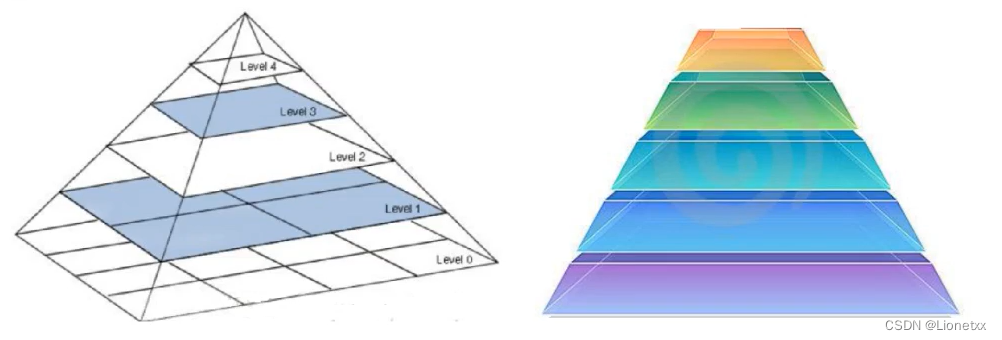
There are two common types of image pyramids ：

• The pyramid of Gauss （Gaussian pyramid）： Used to go down / Downsampling （ Resolution decreases , The picture gets smaller , Go up ）, Is the main image pyramid ;
• The pyramid of Laplace （Laplacian pyramid）： It is used to reconstruct the upper unsampled image from the lower image of the pyramid , In digital image processing, that is, prediction residual , The image can be restored to the greatest extent , Use with Gaussian pyramid

The pyramid of Gauss （Gaussian pyramid）

The pyramid of Gauss It is through Gaussian smoothing and sub sampling （ Take a small piece out of a figure ） A series of gains Down sampling image

Down sampling

The principle is very simple ： As shown in the figure below

Original image resolution M*N ——> Resolution after image processing M/2 * N/2; That is, after each treatment , The result is the original 1/4（ Even numbers are not required , It will automatically round ）

Be careful ： Down sampling （ Resolution decreases , In the above figure, it is shown as Direction up ） Information will be lost

The key API：cv2.pyrDown(src[, dst[, dstsize[, borderType]]])
among ：

• src： Pictures that need to be operated
• dst： Return value , Do not write , We can accept it with a parameter
• dstsize： Returns the size of the picture
• The picture will become the original 1/4

#  The pyramid of Gauss  ——>  Down sampling 

import cv2
import numpy as np

img = cv2.imread('./lena.png')

#  Resolution reduction operation ： Down sampling 
dst = cv2.pyrDown(img)

#  It can be changed many times 
dst2 = cv2.pyrDown(dst)

#  Exhibition 
cv2.imshow('img',img)
cv2.imshow('dst',dst)
cv2.imshow('dst2',dst2)

cv2.waitKey(0)
cv2.destroyAllWindows()

result ：

In fact, the clarity has hardly changed , This is the power of image pyramid ： Even rows and even columns are lost , however After Gaussian kernel convolution , It's equivalent to smoothing a pixel around , Therefore, there is little change

---

Sampling up

Up sampling is the opposite process of down sampling , Refers to the process of the picture from small to large

1. Double the image in each direction , New rows and columns with 0 fill
2. Use the same kernel as before （ multiply 4） Convolute the enlarged image , Get an approximation ——> Suppose a group of four , It is equivalent to turning the place with value to three around 0 Fill in the position of **（ Take the upper left corner for example , Is equivalent to 10 Divide into four , One copy 2.5; But because the overall value becomes smaller , The image will be dimmed , To solve this problem , Let's take 4, amount to “ Copy ” Four copies ）**

The operation is the same as down sampling ！

The key API：cv2.pyrUp(src[, dst[, dstsize[, borderType]]])
among ：

• src： Pictures that need to be operated
• dst： Return value , Do not write , We can accept it with a parameter
• dstsize： Returns the size of the picture
• The picture will become the original 4 times

#  The pyramid of Gauss  ——>  Sampling up 

import cv2
import numpy as np

img = cv2.imread('./Hello.jpeg')

#  Resolution reduction operation ： Down sampling 
dst = cv2.pyrUp(img)

#  It can be changed many times 
# dst2 = cv2.pyrUp(dst)

#  Exhibition 
cv2.imshow('img',img)
cv2.imshow('dst',dst)
# cv2.imshow('dst2',dst2)

cv2.waitKey(0)
cv2.destroyAllWindows()

result ：

---

The pyramid of Laplace

 Laplace pyramid image  =  original image  -  Shangcai operation function （ Mining operation function ( original image )）

The image after downsampling is upsampled , Then make an error with the original image that has not been downsampled before to obtain the residual image ！ Prepare information for restoring images ！

in other words , The pyramid of Laplace It's universal Original image subtract An image that shrinks first and then enlarges （ The pyramid of Gauss ） A series of images of , The result of subtraction is the image of Laplace pyramid . What is retained is the residual ！

Laplace pyramid is made up of Gauss pyramid , There are no special functions

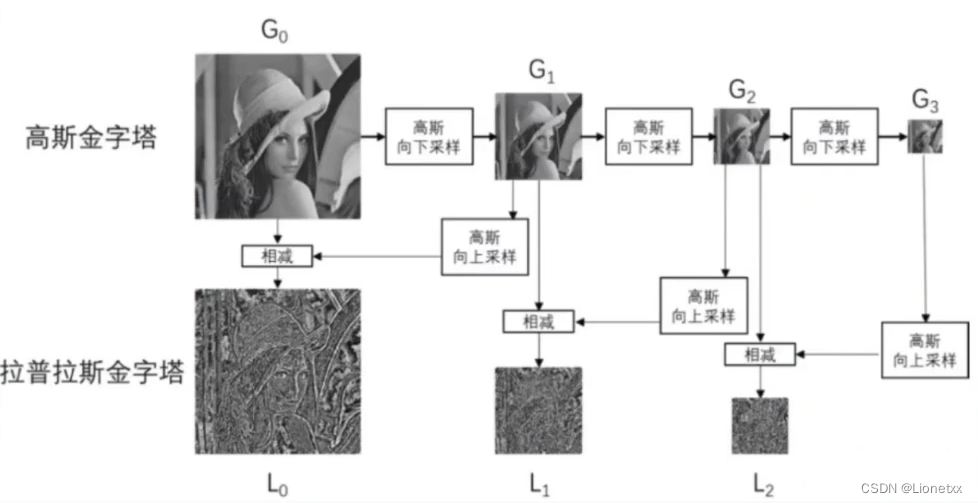
#  The pyramid of Laplace 
#  Original picture  -  Zoom in and out （ In this way, it can be changed back to the original size , Convenient to do bad ）

import cv2
import numpy as np

img = cv2.imread('./lena.png')

#  Shrink first 
temp = cv2.pyrDown(img)

#  Zoom in 
dst = cv2.pyrUp(temp)

#  Original picture   and   The pyramid of Gauss   The difference is   The pyramid of Laplace 
lap0 = img - dst

#  Exhibition 
# cv2.imshow('img',img)
cv2.imshow('dst',dst)
cv2.imshow('lap0',lap0)

cv2.waitKey(0)
cv2.destroyAllWindows()

result ：

---

Image histogram

The basic concept of image histogram

In statistics , Histogram is a graphical representation of the distribution of data , It's a two-dimensional statistical chart

Image histogram Is a histogram used to represent the brightness distribution in a digital image , Plotted The number of pixels per luminance value in the image .

By observing the histogram, you can know how to adjust the histogram of brightness distribution . In this histogram , The left side of the abscissa is solid black 、 Darker areas , and The right side is brighter 、 Pure white areas .

therefore , The data of the image histogram of a darker picture is mostly concentrated in the left and middle parts , And the whole is bright , Images with only a few shadows are the opposite

• Abscissa ： Of each pixel in the image Gray scale （ Gray value 0-255 Every number is a gray level ）
• Ordinate ： With this gray level Number of pixels

We can see from the image histogram ： There are many dark or bright points in this image （ There are many pixels with these gray levels ）, On the contrary, there are fewer points of light dark balance **（ There are fewer pixels with these gray levels ）**

After understanding it, we can independently analyze the following three pictures （ Too lazy to write. …）

---

Take up a ：
There is one 3×3 Pictures of the , among

• Gray level of pixels Express ——> What numbers are there in the picture
• The number of pixels with this gray level Express ——> This number appears several times in the picture

Draw the histogram above , There are many kinds of histograms . such as ：
Broken line diagram ：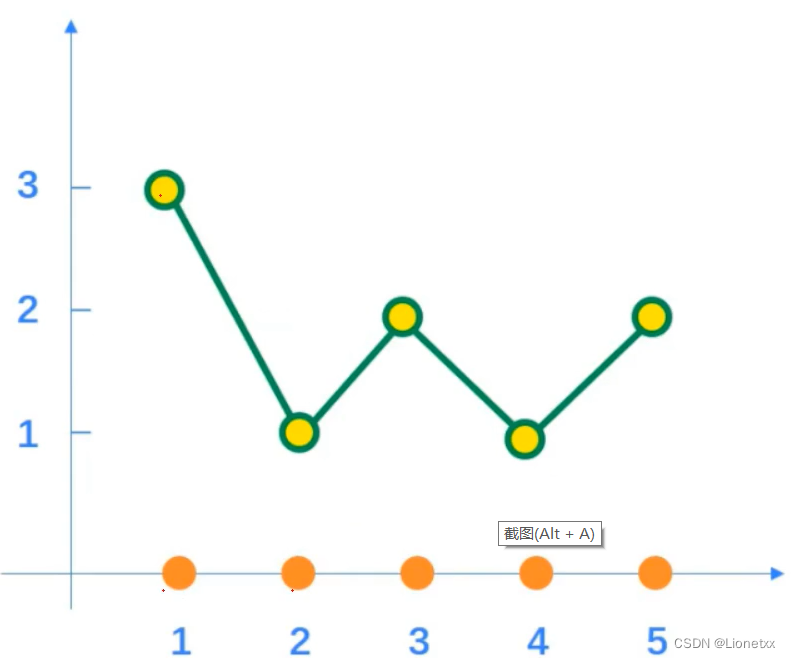

Histogram ：

Normalized graph ：

• Abscissa ： Of each pixel in the image Gray scale （ The pixel value appearing in the image ）
• Ordinate ： This gray level appears probability （ The number of times each pixel value appears in the image / Number of pixel values ）
  

---

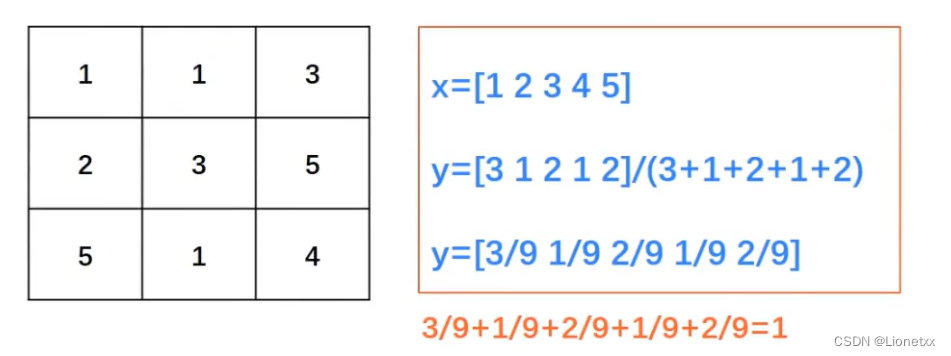
Histogram terminology

• dims： The number of features to be counted in the histogram , That is, the items that need to be counted . Such as dims = 1, It means that we only use the statistical gray value
• bins： Between each cell in the histogram （ Each feature space sub segment ） Number of , Operate more often
  

range： We count the range of gray values , It's usually 0-255

in general ： Histogram is a graph drawn by the number of times various gray levels appear in the image

---

Use OpenCV Statistical histogram

The key API：cv2.calcHist(images, channels, mask, histSize, ranges[, hist[, accumulate]])

• images： original image （ It can not be black and white ）, Add s It means that histogram statistics can be carried out on multiple pictures at the same time ——> Brackets should be added here , The representation is a collection of images
• channels： Designated channel , You need brackets "[ ]" Cover up
  • If the input image is a grayscale image , Then there is only one channel , be [ ] Write in 0：[0]
  • Color images can be [ 0 ], [ 1 ], [ 2 ], They correspond to each other B,G,R
• mask： Mask image
  • Count the histogram of the whole image ： Set to None
  • Statistics of the histogram of an area of the image ： Mask image required
• histSize：BINS（ The column in the histogram ） The number of
  • It needs to be enclosed in brackets , Such as [256]（ Because from 0 Start , So there is 256 A digital ）
• ranges： Pixel value range , for example [0,255]
• accumulate： Cumulative identification
  • The default value is False（ Generally, we only operate on one graph ）
  • If it is set to True, be The histogram will not be cleared at the beginning of allocation
  • This parameter allows the calculation of a single histogram from multiple objects , Or to update histograms in real time
  • Cumulative results of multiple histograms , Used to calculate histogram for a set of images
• This function will return the data of histogram , It can be used directly plt.plot( Return value ) Draw ！

# OpenCV Statistical histogram 

import cv2
import numpy as np

img = cv2.imread('./lena.png')

hist = cv2.calcHist([img],[0],None,[256],[0,255])
print(hist)

result ：

From top to bottom are Gray scale 0、1、2......

---

Use OpenCV Draw histogram

#  Draw histogram 
#  Use Opencv The statistical method of 

import cv2
import numpy as np
import matplotlib.pyplot as plt

img = cv2.imread('./lena.png')

#  Statistical histogram data , Don't do grayscale pictures anymore （ Parameters channels The channel can be counted ）
hist_B = cv2.calcHist([img],[0],None,[256],[0,255])
hist_G = cv2.calcHist([img],[1],None,[256],[0,255])
hist_R = cv2.calcHist([img],[2],None,[256],[0,255])

#  Three data are obtained above , We draw three pictures correspondingly , Mark different colors 
plt.plot(hist_B,color = 'b',label = 'Blue') #  No more hist(), Because what is returned is histogram data 
plt.plot(hist_G,color = 'g',label = 'Green')
plt.plot(hist_R,color = 'r',label = 'Red')
plt.legend() #  Put instructions on the shaft 
#  Exhibition （ Add it or not ）
plt.show()

result ：
The corresponding horizontal axis is converted from gray value （ We don't give the value of the horizontal axis ,matplotlib Automatically indexed , amount to cv2.cvtColor(img,cv2.COLOR_GRAY2BRR)）

We can find out ： The whole picture is red （ Red low frequency is less , There are many in the high-frequency region ）, Blue is on the low side （ Only a little on the hat ）, Green is less in the high frequency region （ There is almost no green in the whole picture ）

---

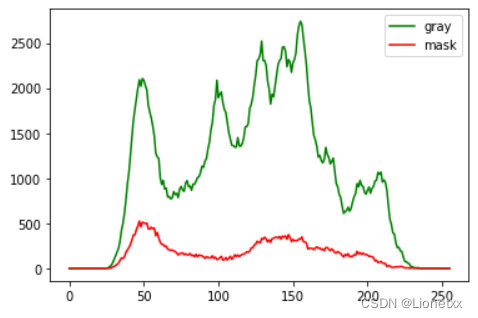
Use the histogram of the mask

If you are only interested in a certain part of the picture （ For example, the face in the image 、 hand …）, You can use it A mask To operate , Select roi Area , Use for this area cv2.calcHist(mask) Histogram calculation

• A mask
  
  Characteristics of mask ： The area you want to display is pure white , Other areas you don't want it to display are pure black
• How to generate a mask
  • Mr. Cheng is the same size as the original picture （img.shape） All black pictures of ：mask = np.zeros(image.shape,np.uint8)
  • Set the desired region as 255：mask[100:200,200:300] = 355

#  Use the histogram of the mask 

import cv2
import numpy as np
import matplotlib.pyplot as plt

img = cv2.imread('./lena.png')

#  Turn into a black-and-white picture 
gray = cv2.cvtColor(img,cv2.COLOR_BGR2GRAY)  

#  Generate mask image 
mask = np.zeros(gray.shape,np.uint8) #  Generate an all black graph with the same size as the original one  uint8：8 Bits are all used to represent numbers 

#  Set the area where you want to count the histogram (roi)
mask[200:400,200:400] = 255

#  Statistical histogram data  ——>  Compare the original image with the data after mask operation 
hist_gray = cv2.calcHist([gray],[0],None,[256],[0,255])
hist_mask = cv2.calcHist([gray],[0],mask,[256],[0,255])

#  Use matplotlib Draw a histogram 
plt.plot(hist_gray,label = 'gray',color = 'g')
plt.plot(hist_mask,label = 'mask',color = 'r')
plt.legend()
plt.show()

##---------------------------------------------------------------------------------------------
#  We want to see the effect of the mask in the picture in advance 
cv2.imshow('gray',gray)
cv2.imshow('mask',mask)

# gray  and  gray  And the result of the operation is itself  mask The role of ： First do and operation , The results will be compared with mask Do with the operation 
#  Characteristics of and operation ： Two numbers “ And ”,0 And any number is 0,255 He Fei 0 Of “ And ” are 0 In itself （ Original picture ）
cv2.imshow('gray&mask',cv2.bitwise_and(gray,gray,mask = mask))
##---------------------------------------------------------------------------------------------

#  Exit conditions 
cv2.waitKey(0)
cv2.destroyAllWindows()

result ：