当前位置:网站首页>[digital signal processing] basic sequence (basic sequence lists | unit pulse sequence | unit pulse function | discrete unit pulse function | difference between unit pulse function and discrete unit p
[digital signal processing] basic sequence (basic sequence lists | unit pulse sequence | unit pulse function | discrete unit pulse function | difference between unit pulse function and discrete unit p
2022-06-26 06:34:00 【Hanshuliang】
List of articles
One 、 Basic sequence enumeration
Basic sequence Yes
- Unit pulse sequence
- Unit step sequence
- Rectangular sequence
- Real exponential sequence
- Sinusoidal sequence
- Complex exponential sequence
Two 、 Unit pulse sequence
Unit pulse sequence :
δ ( n ) = { 1 n = 0 0 n = 1 \delta (n) = \begin{cases} 1 \ \ \ \ n = 0 \\ \\ 0 \ \ \ \ n = 1 \end{cases} δ(n)=⎩⎪⎨⎪⎧1 n=00 n=1
1、 Unit pulse function
Unit pulse function ( Unit impulse function ) Corresponding Function image as follows : The horizontal axis is n n n , The vertical axis is δ ( n ) \delta (n) δ(n) ;
- n = 0 n = 0 n=0 when , δ ( n ) = 1 \delta (n) = 1 δ(n)=1
- n = 1 n = 1 n=1 when , δ ( n ) = 0 \delta (n) = 0 δ(n)=0

2、 Discrete unit impulse function
Here pay attention to and " Discrete unit impulse function " Distinguish , I added " discrete " Two words , Its value is no longer fixed 0 , 1 0 , 1 0,1 ;
Discrete unit impulse function ( Discrete unit impulse function ) Corresponding Function image as follows : The horizontal axis is t t t , The vertical axis is δ ( t ) \delta (t) δ(t) ;
- t = 0 t = 0 t=0 when , δ ( t ) \delta (t) δ(t) Is infinite
- t = 1 t = 1 t=1 when , δ ( t ) = 0 \delta (t) = 0 δ(t)=0

3、 Unit pulse function And The difference between discrete unit impulse functions
Unit pulse function And Discrete unit impulse function The difference between :
① The horizontal axis coordinate is 0 The situation of :
stay Unit pulse function δ ( n ) \delta (n) δ(n) in , n = 0 n = 0 n=0 when , δ ( n ) = 1 \delta (n) = 1 δ(n)=1
stay Discrete unit impulse function δ ( t ) \delta (t) δ(t) in , t = 0 t = 0 t=0 when , δ ( t ) \delta (t) δ(t) Is infinite ;
② The vertical axis coordinate is 0 The situation of , That is, the function is 0 0 0 The situation of :
stay Unit pulse function δ ( n ) \delta (n) δ(n) in , stay n = ⋯ , − 3 , − 2 , − 1 , 1 , 2 , 3 , ⋯ n = \cdots , -3 , -2, -1 , 1, 2, 3, \cdots n=⋯,−3,−2,−1,1,2,3,⋯ The value at the position of an equal integer is 0 0 0 ;
stay Discrete unit impulse function δ ( t ) \delta (t) δ(t) in , t t t Divide by 0 0 0 Any value other than , The corresponding function value δ ( t ) \delta (t) δ(t) All for 0 0 0 ;
③ Whether it can be realized :
Unit pulse function δ ( n ) \delta (n) δ(n) It is physically achievable ;
Discrete unit impulse function δ ( t ) \delta (t) δ(t) Physically impossible ;
边栏推荐
- 同步通信和异步通信的区别以及优缺点
- How to make the main thread wait for the sub thread to execute before executing
- 视图简析
- EFK升级到ClickHouse的日志存储实战
- Gof23 - builder mode
- Mysql delete in 不走索引的
- Comparison between Prometheus and ZABBIX
- MYSQL触发器要如何设置,简单教程新手一看就会
- Playing RTSP streaming video on Web pages (webrtc)
- Five solutions across domains
猜你喜欢

GoF23—原型模式
Experience the new features of Milvus 2.0 together

Design and practice of low code real-time data warehouse construction system
Alarm operation and Maintenance Center | build an efficient and accurate alarm collaborative processing system

When vs code uses prettier to format JS, there is a space between the name of the function definition and the parentheses, and ESLIt does not allow this space

TCP connection and disconnection, detailed explanation of state transition diagram
Logstash -- send an alert message to the nail using the throttle filter
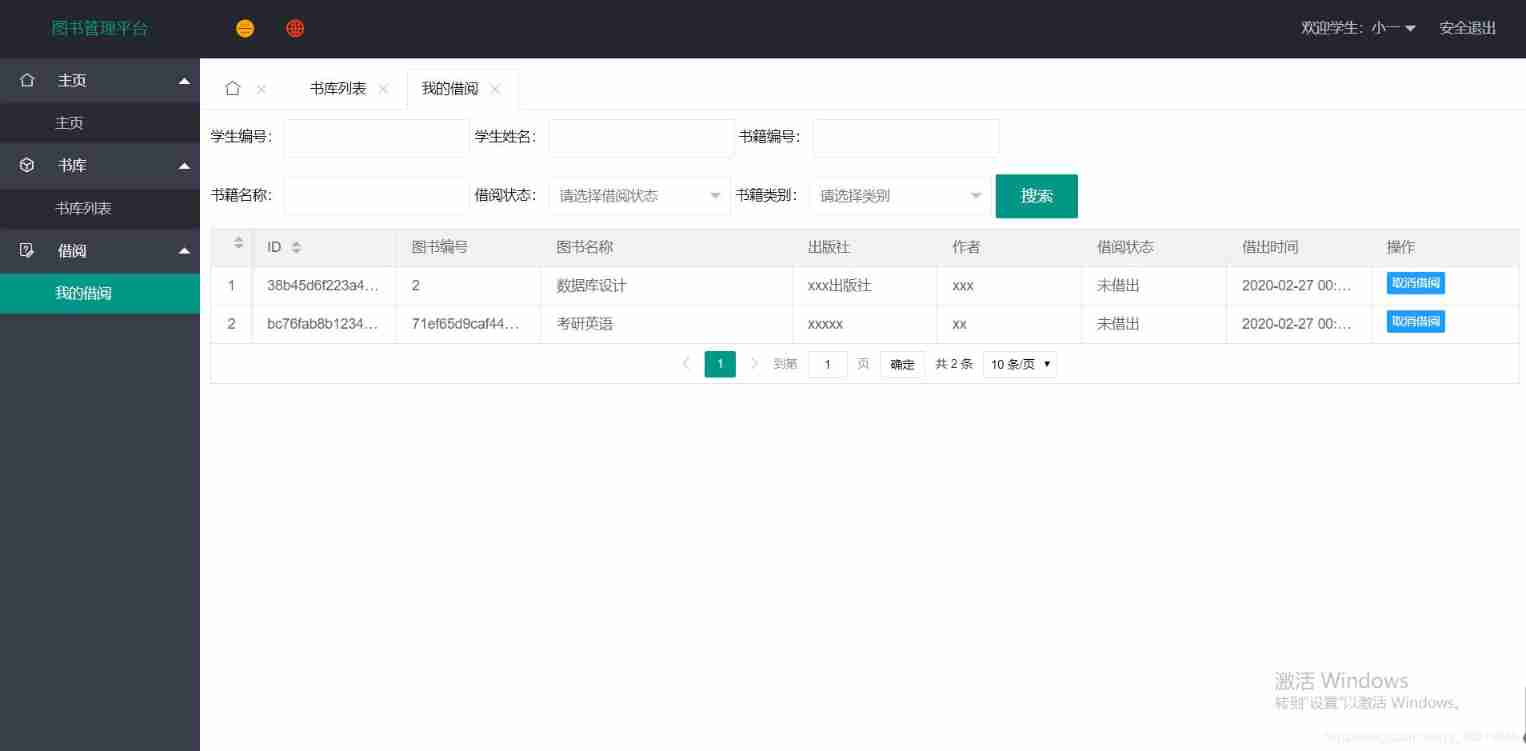
Library management system

营销技巧:相比较讲产品的优点,更有效的是要向客户展示使用效果
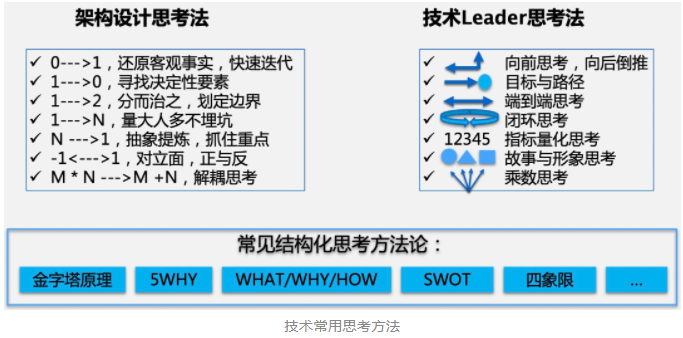
架构设计方法
随机推荐
稀疏数组sparsearray
Go语言学习笔记 1.2-变量篇
Print bit information of numbers
Data visualization practice: Data Visualization
TCP連接與斷開,狀態遷移圖詳解
Web components series (10) -- realize the basic layout of mycard
如何设计好的技术方案
Laravel 实现 groupBy 查询分组数量
GoF23—抽象工厂模式
Gof23 - abstract factory pattern
Message queue - message transaction management comparison
Connexion et déconnexion TCP, détails du diagramme de migration de l'état
Gof23 - prototype mode
Evolution history of qunar Bi platform construction
Zotero文献管理工具之Jasminum(茉莉花)插件
GoF23—建造者模式
Import / export function implementation
寶塔服務器搭建及數據庫遠程連接
Playing RTSP streaming video on Web pages (webrtc)
Requirement analysis of personal blog system

