当前位置:网站首页>Deriving Kalman filter from probability theory
Deriving Kalman filter from probability theory
2022-06-11 21:08:00 【Server 1703 not found】
List of articles
In this paper, the scalar and vector Kalman filter is derived from some properties of joint normal distribution . Some of the following properties have been named for convenience , Not necessarily a formal academic name .
ps: There are several properties I can't prove , Welcome to correct .
The official certificate has not been written yet .
Description of formulas and symbols
Discrete systems
x ( k ) = A x ( k − 1 ) + B u ( k − 1 ) + v ( k − 1 ) y ( k ) = C x ( k ) + W ( k ) \begin{aligned} & x(k)=Ax(k-1)+Bu(k-1)+v(k-1) \\ & y(k)=Cx(k)+W(k) \end{aligned} x(k)=Ax(k−1)+Bu(k−1)+v(k−1)y(k)=Cx(k)+W(k)
among V , W V,W V,W Is the covariance matrix of zero mean Gaussian white noise .
The recurrence formula of Kalman filter is as follows
x ^ ( k ∣ k − 1 ) = A x ^ ( k − 1 ) + B u ( k − 1 ) x ^ ( k ) = x ^ ( k ∣ k − 1 ) + K ( k ) [ y ( k ) − C x ^ ( k ∣ k − 1 ) ] P ( k ∣ k − 1 ) = A P ( k − 1 ) A T + V P ( k ) = [ I − K ( k ) C ] P ( k ∣ k − 1 ) K ( k ) = P ( k ∣ k − 1 ) C T [ C P ( k ∣ k − 1 ) C T + W ] − 1 \begin{aligned} & \hat{x}(k|k-1)=A\hat{x}(k-1)+Bu(k-1) \\ & \hat{x}(k)=\hat{x}(k|k-1)+K(k)[y(k)-C\hat{x}(k|k-1)] \\ & P(k|k-1)=AP(k-1)A^{\text{T}}+V \\ & P(k)=[I-K(k)C]P(k|k-1) \\ & K(k)=P(k|k-1)C^{\text{T}}[CP(k|k-1)C^{\text{T}}+W]^{-1} \\ \end{aligned} x^(k∣k−1)=Ax^(k−1)+Bu(k−1)x^(k)=x^(k∣k−1)+K(k)[y(k)−Cx^(k∣k−1)]P(k∣k−1)=AP(k−1)AT+VP(k)=[I−K(k)C]P(k∣k−1)K(k)=P(k∣k−1)CT[CP(k∣k−1)CT+W]−1
- Y ( k ) = [ y ( 0 ) , y ( 1 ) , ⋯ , y ( k ) ] \mathbf{Y}(k)=[y(0),y(1),\cdots,y(k)] Y(k)=[y(0),y(1),⋯,y(k)] Before presentation k k k Observation data at a time
- x ^ ( k ) = E [ x ( k ) ∣ Y ( k ) ] \hat{x}(k)=\text{E}[x(k)|Y(k)] x^(k)=E[x(k)∣Y(k)] According to the previous k k k Prediction of observed data at a time x ( k ) x(k) x(k)
- x ^ ( k ∣ k − 1 ) \hat{x}(k|k-1) x^(k∣k−1) According to the previous k − 1 k-1 k−1 Prediction of observed data at a time x ( k ) x(k) x(k)
- P ( k ) P(k) P(k) Indicates the estimation error
- P ( k ∣ k − 1 ) P(k|k-1) P(k∣k−1) Represents the prediction error
Several properties and partial proofs
Bayesian least mean square error estimator (Bmse)
Observed x x x after θ \theta θ The least mean square error estimator of θ ^ \hat{\theta} θ^ by
θ ^ = E ( θ ∣ x ) \hat{\theta}=\text{E}(\theta|x) θ^=E(θ∣x)
The main idea of proof is to find θ ^ \hat{\theta} θ^ Minimize the minimum mean square error . prove :
Bmse ( θ ^ ) = E [ ( θ − θ ^ ) 2 ] = ∬ ( θ − θ ^ ) 2 p ( x , θ ) d x d θ = ∫ [ ∫ ( θ − θ ^ ) 2 p ( θ ∣ x ) d θ ] p ( x ) d x J = ∫ ( θ − θ ^ ) 2 p ( θ ∣ x ) d θ ∂ J ∂ θ ^ = − 2 ∫ θ p ( θ ∣ x ) d θ + 2 θ ^ ∫ p ( θ ∣ x ) d θ = 0 θ ^ = 2 ∫ θ p ( θ ∣ x ) d θ 2 ∫ p ( θ ∣ x ) d θ = E ( θ ∣ x ) \begin{aligned} \text{Bmse}(\hat{\theta}) &= \text{E}[(\theta-\hat{\theta})^2] \\ &= \iint(\theta-\hat{\theta})^2p(x,\theta)\text{d}x\text{d}\theta \\ &=\int\left[\int(\theta-\hat{\theta})^2p(\theta|x)\text{d}\theta\right] p(x)\text{d}x \\ J &= \int(\theta-\hat{\theta})^2p(\theta|x)\text{d}\theta \\ \frac{\partial J}{\partial\hat{\theta}} &= -2\int\theta p(\theta|x)\text{d}\theta +2\hat{\theta}\int p(\theta|x)\text{d}\theta=0 \\ \hat{\theta} &= \frac{2\displaystyle\int\theta p(\theta|x)\text{d}\theta} {2\displaystyle\int p(\theta|x)\text{d}\theta}=\text{E}(\theta|x) \\ \end{aligned} Bmse(θ^)J∂θ^∂Jθ^=E[(θ−θ^)2]=∬(θ−θ^)2p(x,θ)dxdθ=∫[∫(θ−θ^)2p(θ∣x)dθ]p(x)dx=∫(θ−θ^)2p(θ∣x)dθ=−2∫θp(θ∣x)dθ+2θ^∫p(θ∣x)dθ=0=2∫p(θ∣x)dθ2∫θp(θ∣x)dθ=E(θ∣x)
Zero mean application theorem ( Scalar form )
set up x x x and y y y Is a random variable with joint normal distribution , be
E ( y ∣ x ) = E y + Cov ( x , y ) D x ( x − E x ) D ( y ∣ x ) = D y − Cov 2 ( x , y ) D x \begin{aligned} & \text{E}(y|x)=\text{E}y+\frac{\text{Cov}(x,y)}{\text{D}x}(x-\text{E}x) \\ & \text{D}(y|x)=\text{D}y-\frac{\text{Cov}^2(x,y)}{\text{D}x} \\ \end{aligned} E(y∣x)=Ey+DxCov(x,y)(x−Ex)D(y∣x)=Dy−DxCov2(x,y)
The two forms can be written separately
y ^ − E y D y = ρ x − E x D x D ( y ∣ x ) = D y ( 1 − ρ 2 ) \begin{aligned} & \frac{\hat{y}-\text{E}y}{\sqrt{\text{D}y}} =\rho\frac{x-\text{E}x}{\sqrt{\text{D}x}} \\ & \text{D}(y|x)=\text{D}y(1-\rho^2) \\ \end{aligned} Dyy^−Ey=ρDxx−ExD(y∣x)=Dy(1−ρ2)
prove :
y ^ = a x + b J = E ( y − y ^ ) 2 = E [ y 2 − 2 y ( a x + b ) + ( a x + b ) 2 ] = y 2 − 2 E x y ⋅ a − 2 E y ⋅ b + E x 2 ⋅ a 2 + 2 E x ⋅ a b + b 2 d J = ( − 2 E x y + 2 E x 2 + 2 b E x ) d a + ( − 2 E y + 2 a E x + 2 b ) d b ∂ J ∂ a = − 2 E x y + 2 E x 2 + 2 b E x = 0 ∂ J ∂ b = − 2 E y + 2 a E x + 2 b = 0 b = E x y − E x 2 E x a = E y − b E x = E x E y − E x y + E x 2 ( E x ) 2 y ^ = a x + b = \begin{aligned} \hat{y} &= ax+b \\ J &= \text{E}(y-\hat{y})^2 \\ &= \text{E}[y^2-2y(ax+b)+(ax+b)^2] \\ &= y^2-2\text{E}xy\cdot a-2\text{E}y\cdot b +\text{E}x^2\cdot a^2+2\text{E}x\cdot ab+b^2 \\ \text{d}J &= (-2\text{E}xy+2\text{E}x^2+2b\text{E}x)\text{d}a +(-2\text{E}y+2a\text{E}x+2b)\text{d}b \\ \frac{\partial J}{\partial a} &= -2\text{E}xy+2\text{E}x^2+2b\text{E}x = 0 \\ \frac{\partial J}{\partial b} &= -2\text{E}y+2a\text{E}x+2b = 0 \\ b &= \frac{\text{E}xy-\text{E}x^2}{\text{E}x} \\ a &= \frac{\text{E}y-b}{\text{E}x} = \frac{\text{E}x\text{E}y-\text{E}xy+\text{E}x^2}{(\text{E}x)^2} \\ \hat{y} &= ax+b = \\ \end{aligned} y^JdJ∂a∂J∂b∂Jbay^=ax+b=E(y−y^)2=E[y2−2y(ax+b)+(ax+b)2]=y2−2Exy⋅a−2Ey⋅b+Ex2⋅a2+2Ex⋅ab+b2=(−2Exy+2Ex2+2bEx)da+(−2Ey+2aEx+2b)db=−2Exy+2Ex2+2bEx=0=−2Ey+2aEx+2b=0=ExExy−Ex2=ExEy−b=(Ex)2ExEy−Exy+Ex2=ax+b=
The theorem is only valid for random variables that satisfy linear relations including normal distribution ( It is not clear where the linearity is satisfied ). for example , For two joint uniform distributions
f ( x , y ) = 2 , 0 < x < 1 , 0 < y < x f ( x , y ) = 3 , 0 < x < 1 , x 2 < y < x \begin{aligned} & f(x,y)=2,\quad 0<x<1,0<y<x \\ & f(x,y)=3,\quad 0<x<1,x^2<y<\sqrt{x} \end{aligned} f(x,y)=2,0<x<1,0<y<xf(x,y)=3,0<x<1,x2<y<x
The first was established , The second one does not hold because of the existence of nonlinearity , in other words y y y In the data x x x The linear Bayesian estimator under is not the best estimator , The two are
y ^ = E y + Cov ( x , y ) D x ( x − E x ) = 133 x + 9 153 y ^ = E ( y ∣ x ) = x + x 2 2 \begin{aligned} & \hat{y}=\text{E}y+\frac{\text{Cov}(x,y)}{\text{D}x}(x-\text{E}x) =\frac{133x+9}{153} \\ & \hat{y}=\text{E}(y|x)=\frac{\sqrt{x}+x^2}{2} \\ \end{aligned} y^=Ey+DxCov(x,y)(x−Ex)=153133x+9y^=E(y∣x)=2x+x2
Zero mean application theorem ( Vector form )
x \boldsymbol{x} x and y \boldsymbol{y} y Is a random vector of joint normal distribution , x \boldsymbol{x} x yes m×1, y \boldsymbol{y} y yes n×1, Block covariance matrix
C = [ C x x C x y C y x C y y ] \mathbf{C}=\left[\begin{matrix} \mathbf{C}_{xx} & \mathbf{C}_{xy} \\ \mathbf{C}_{yx} & \mathbf{C}_{yy} \end{matrix}\right] C=[CxxCyxCxyCyy]
be
E ( y ∣ x ) = E ( y ) + C y x C x x − 1 ( x − E ( x ) ) \text{E}(\boldsymbol{y}|\boldsymbol{x})=\text{E}(\boldsymbol{y}) +\mathbf{C}_{yx}\mathbf{C}_{xx}^{-1}(\boldsymbol{x}-\text{E}(\boldsymbol{x})) E(y∣x)=E(y)+CyxCxx−1(x−E(x))
among C x y C_{xy} Cxy Express Cov ( x , y ) \text{Cov}(x,y) Cov(x,y). prove :
y ^ = A x + b J = E ( y − y ^ ) ⊤ ( y − y ^ ) = E ( y ⊤ y − y ^ ⊤ y − y ⊤ y ^ + y ^ ⊤ y ^ ) d J = dE ( − y ^ ⊤ y − y ⊤ y ^ + y ^ ⊤ y ^ ) = dE [ tr ( − y ^ ⊤ y − y ⊤ y ^ + y ^ ⊤ y ^ ) ] = ⋯ A = C x x − 1 C x y b = E y − A E x y ^ = C x x − 1 C x y x + E y − C x x − 1 C x y E x = E y + C x x − 1 C x y ( x − E x ) \begin{aligned} \hat{y} &= Ax+b \\ J &= \text{E}(y-\hat{y})^{\top}(y-\hat{y}) \\ &= \text{E}(y^{\top}y-\hat{y}^{\top}y-y^{\top}\hat{y}+\hat{y}^{\top}\hat{y}) \\ \text{d}J &= \text{dE}(-\hat{y}^{\top}y-y^{\top}\hat{y}+\hat{y}^{\top}\hat{y}) \\ &= \text{dE}[\text{tr}(-\hat{y}^{\top}y-y^{\top}\hat{y}+\hat{y}^{\top}\hat{y})] \\ &= \cdots \\ A &= C_{xx}^{-1}C_{xy} \\ b &= \text{E}y-A\text{E}x \\ \hat{y} &= C_{xx}^{-1}C_{xy}x+\text{E}y-C_{xx}^{-1}C_{xy}\text{E}x \\ &= \text{E}y+C_{xx}^{-1}C_{xy}(x-\text{E}x) \\ \end{aligned} y^JdJAby^=Ax+b=E(y−y^)⊤(y−y^)=E(y⊤y−y^⊤y−y⊤y^+y^⊤y^)=dE(−y^⊤y−y⊤y^+y^⊤y^)=dE[tr(−y^⊤y−y⊤y^+y^⊤y^)]=⋯=Cxx−1Cxy=Ey−AEx=Cxx−1Cxyx+Ey−Cxx−1CxyEx=Ey+Cxx−1Cxy(x−Ex)
Projection theorem ( Orthogonal principle )
When using the linear combination of data samples to estimate a random variable , When the error between the estimated value and the true value is orthogonal to each data sample , This estimate is the best estimate , Data samples x x x And the best estimator y ^ \hat{y} y^ Satisfy
E [ ( y − y ^ ) ⊤ x ( n ) ] = 0 n = 0 , 1 , ⋯ , N − 1 \text{E}[(y-\hat{y})^\top x(n)]=0\quad n=0,1,\cdots,N-1 E[(y−y^)⊤x(n)]=0n=0,1,⋯,N−1
Random variables with zero mean satisfy the properties in inner product space . Define the length of the variable ∣ ∣ x ∣ ∣ = E x 2 ||x||=\sqrt{\text{E}x^2} ∣∣x∣∣=Ex2, Variable x x x and y y y Inner product ( x , y ) (x,y) (x,y) Defined as E ( x y ) \text{E}(xy) E(xy), The angle between two variables is defined as the correlation coefficient ρ \rho ρ. When E ( x y ) = 0 \text{E}(xy)=0 E(xy)=0 Time variable x x x and y y y orthogonal .
When the mean value is not zero , Define the length of the variable ∣ ∣ x ∣ ∣ = D x ||x||=\sqrt{\text{D}x} ∣∣x∣∣=Dx, Variable x x x and y y y Inner product ( x , y ) (x,y) (x,y) Defined as Cov ( x y ) \text{Cov}(xy) Cov(xy), The angle between two variables is defined as the correlation coefficient ρ \rho ρ. The case that the mean value is not zero is my own guess , A lot of information is not detailed , But the derivation of Kalman filter is all non-zero mean .
take x x x and y y y Corresponding to the form of data , namely x ( 0 ) x(0) x(0) yes x x x, x ( 1 ) x(1) x(1) yes y y y, x ^ ( 1 ∣ 0 ) \hat{x}(1|0) x^(1∣0) yes y ^ \hat{y} y^, obtain
E [ ( x ( 1 ) − x ^ ( 1 ∣ 0 ) ) ⊤ x ( 0 ) ] = 0 \text{E}[(x(1)-\hat{x}(1|0))^\top x(0)]=0 E[(x(1)−x^(1∣0))⊤x(0)]=0
among
x ~ ( k ∣ k − 1 ) = x ( k ) − x ^ ( k ∣ k − 1 ) \widetilde{x}(k|k-1) = x(k)-\hat{x}(k|k-1) x(k∣k−1)=x(k)−x^(k∣k−1)
It is called new interest (innovation), With old data x ( 0 ) x(0) x(0) orthogonal .
Scalar formal proof :
E [ x ( y ^ − y ) ] = E [ x E y + Cov ( x , y ) D x ( x 2 − x E x ) − x y ] = E x E y + Cov ( x , y ) D x ( E x 2 − ( E x ) 2 ) − E x y = Cov ( x , y ) + E x E y − E x y = 0 \begin{aligned} \text{E}[x(\hat{y}-y)] &= \text{E}[x\text{E}y +\frac{\text{Cov}(x,y)}{\text{D}x}(x^2-x\text{E}x)-xy] \\ &= \text{E}x\text{E}y +\frac{\text{Cov}(x,y)}{\text{D}x}(\text{E}x^2-(\text{E}x)^2)-\text{E}xy \\ &= \text{Cov}(x,y)+\text{E}x\text{E}y-\text{E}xy=0 \end{aligned} E[x(y^−y)]=E[xEy+DxCov(x,y)(x2−xEx)−xy]=ExEy+DxCov(x,y)(Ex2−(Ex)2)−Exy=Cov(x,y)+ExEy−Exy=0
Vector form proof :
E [ x ⊤ ( y ^ − y ) ] = E [ x ⊤ E y + x ⊤ C x x − 1 C x y ( x − E x ) ] = ⋯ = 0 \begin{aligned} \text{E}[x^\top(\hat{y}-y)] &= \text{E}[x^\top\text{E}y+x^\top C_{xx}^{-1}C_{xy}(x-\text{E}x)] \\ &= \cdots \\ &= 0 \end{aligned} E[x⊤(y^−y)]=E[x⊤Ey+x⊤Cxx−1Cxy(x−Ex)]=⋯=0
because E ( y − y ^ ) = 0 \text{E}(y-\hat{y})=0 E(y−y^)=0, Therefore, the orthogonal condition also holds when the mean value is non-zero . Another formula of projection theorem can be obtained from graph
E [ ( y − y ^ ) y ^ ] = 0 \text{E}[(y-\hat{y})\hat{y}]=0 E[(y−y^)y^]=0
prove :
E [ y ^ ( y ^ − y ) ] = E [ ( E y + k x − k E x ) ( E y + k x − k E x − y ) ] = ( E y ) 2 + k E x E y − k E x E y − ( E y ) 2 + k E x E y + k 2 E x 2 − k 2 ( E x ) 2 − k E x y − k E x E y − k 2 ( E x ) 2 + k 2 ( E x ) 2 + k E x E y = k 2 D x − k Cov ( x , y ) = [ Cov ( x , y ) ] 2 [ D x ] 2 D x − Cov ( x , y ) D x Cov ( x , y ) = 0 \begin{aligned} & \text{E}[\hat{y}(\hat{y}-y)] \\ =& \text{E}[(\text{E} y+k x-k \text{E} x)(\text{E} y+k x-k \text{E} x-y)] \\ =& (\text{E}y)^{2}+k\text{E}x\text{E}y-k\text{E}x\text{E}y-(\text{E}y)^{2}\\ &+ k\text{E}x\text{E}y+k^{2}Ex^2-k^{2}(\text{E}x)^{2}-k\text{E}xy \\ &- k\text{E}x\text{E}y-k^{2}(\text{E}x)^{2}+k^{2}(\text{E}x)^{2}+k\text{E}x\text{E}y \\ =& k^{2}\text{D}x-k\text{Cov}(x,y) \\ =& \frac{[\text{Cov}(x,y)]^2}{[\text{D}x]^2}\text{D}x-\frac{\text{Cov}(x,y)}{\text{D}x}\text{Cov}(x,y) \\ =&0 \end{aligned} =====E[y^(y^−y)]E[(Ey+kx−kEx)(Ey+kx−kEx−y)](Ey)2+kExEy−kExEy−(Ey)2+kExEy+k2Ex2−k2(Ex)2−kExy−kExEy−k2(Ex)2+k2(Ex)2+kExEyk2Dx−kCov(x,y)[Dx]2[Cov(x,y)]2Dx−DxCov(x,y)Cov(x,y)0
Expected additivity
E [ y 1 + y 2 ∣ x ] = E [ y 1 ∣ x ] + E [ y 2 ∣ x ] \text{E}[y_1+y_2|x]=\text{E}[y_1|x]+\text{E}[y_2|x] E[y1+y2∣x]=E[y1∣x]+E[y2∣x]
Independent conditional additivity
if x 1 x_1 x1 and x 2 x_2 x2 Independent , be
E [ y ∣ x 1 , x 2 ] = E [ y ∣ x 1 ] + E [ y ∣ x 2 ] − E y \text{E}[y|x_1,x_2]=\text{E}[y|x_1]+\text{E}[y|x_2]-\text{E}y E[y∣x1,x2]=E[y∣x1]+E[y∣x2]−Ey
prove :
Make x = [ x 1 ⊤ , x 2 ⊤ ] ⊤ x=[x_1^\top,x_2^\top]^\top x=[x1⊤,x2⊤]⊤, be
C x x − 1 = [ C x 1 x 1 C x 1 x 2 C x 2 x 1 C x 2 x 2 ] − 1 = [ C x 1 x 1 − 1 O O C x 2 x 2 − 1 ] C y x = [ C y x 1 C y x 2 ] E ( y ∣ x ) = E y + C y x C x x − 1 ( x − E x ) = E y + [ C y x 1 C y x 2 ] [ C x 1 x 1 − 1 O O C x 2 x 2 − 1 ] [ x 1 − E x 1 x 2 − E x 2 ] = E [ y ∣ x 1 ] + E [ y ∣ x 2 ] − E y \begin{aligned} C_{xx}^{-1} &= \left[\begin{matrix} C_{x_1x_1} & C_{x_1x_2} \\ C_{x_2x_1} & C_{x_2x_2} \end{matrix}\right]^{-1} = \left[\begin{matrix} C_{x_1x_1}^{-1} & O \\ O & C_{x_2x_2}^{-1} \end{matrix}\right] \\ C_{yx} &= \left[\begin{matrix} C_{yx_1} & C_{yx_2} \end{matrix}\right] \\ \text{E}(y|x) &= \text{E}y+C_{yx}C_{xx}^{-1}(x-\text{E}x) \\ &= \text{E}y+\left[\begin{matrix} C_{yx_1} & C_{yx_2} \end{matrix}\right] \left[\begin{matrix} C_{x_1x_1}^{-1} & O \\ O & C_{x_2x_2}^{-1} \end{matrix}\right] \left[\begin{matrix} x_1-\text{E}x_1 \\ x_2-\text{E}x_2 \end{matrix}\right] \\ &= \text{E}[y|x_1]+\text{E}[y|x_2]-\text{E}y \end{aligned} Cxx−1CyxE(y∣x)=[Cx1x1Cx2x1Cx1x2Cx2x2]−1=[Cx1x1−1OOCx2x2−1]=[Cyx1Cyx2]=Ey+CyxCxx−1(x−Ex)=Ey+[Cyx1Cyx2][Cx1x1−1OOCx2x2−1][x1−Ex1x2−Ex2]=E[y∣x1]+E[y∣x2]−Ey
Dependent conditional additivity ( Innovation theorem )
if x 1 x_1 x1 and x 2 x_2 x2 Not independent , According to the projection theorem x 2 x_2 x2 And x 1 x_1 x1 Independent components x ~ 2 \widetilde{x}_2 x2, Satisfy
E [ y ∣ x 1 , x 2 ] = E [ y ∣ x 1 , x ~ 2 ] = E [ y ∣ x 1 ] + E [ y ∣ x ~ 2 ] − E y \text{E}[y|x_1,x_2] =\text{E}[y|x_1,\widetilde{x}_2] =\text{E}[y|x_1]+\text{E}[y|\widetilde{x}_2]-\text{E}y E[y∣x1,x2]=E[y∣x1,x2]=E[y∣x1]+E[y∣x2]−Ey
among x ~ 2 = x 2 − x ^ 2 = x 2 − E ( x 1 ∣ x 2 ) \widetilde{x}_2=x_2-\hat{x}_2=x_2-\text{E}(x_1|x_2) x2=x2−x^2=x2−E(x1∣x2), By the projection theorem , x 1 x_1 x1 And x ~ 2 \widetilde{x}_2 x2 Independent , x ~ 2 \widetilde{x}_2 x2 It is called new interest .
prove ( Each of the following formulas is to find the part first and then the whole , For ease of understanding, you can look from bottom to top ):
E ( y ∣ x 1 , x 2 ) = E y + [ C y x 1 C y x 2 ] D x 1 D x 2 − C x 1 x 2 2 [ D x 2 − C x 1 x 2 − C x 1 x 2 D x 1 ] [ x 1 − E x 1 x 2 − E x 2 ] Cov ( y , x ^ 2 ) = E [ y ( E x 2 + Cov ( x 2 , x 1 ) D x 1 ( x 1 − E x 1 ) ) ] − E y E x ^ 2 = E y E x 2 + Cov ( x 2 , x 1 ) D x 1 ( E x 1 y − E x 1 E y ) − E y E x 2 = C x 1 x 2 C y x 1 D x 1 Cov ( x 2 , x ^ 2 ) = E x 2 x ^ 2 − E x 2 E x ^ 2 = E [ x 2 ( E x 2 + Cov ( x 2 , x 1 ) D x 1 ( x 1 − E x 1 ) ) ] − ( E x 2 ) 2 = C x 1 x 2 2 D x 1 D x ^ 2 = D ( E x 2 + Cov ( x 2 , x 1 ) D x 1 ( x 1 − E x 1 ) ) = C x 1 x 2 2 ( D x 1 ) 2 D x 1 = C x 1 x 2 2 D x 1 D x ~ 2 = D x 2 + D x ^ 2 − 2 Cov ( x 2 , x ^ 2 ) = D x 2 − C x 1 x 2 2 D x 1 E [ y ∣ x 1 ] + E [ y ∣ x ~ 2 ] − E y = E y + C x 1 y D x 1 ( x 1 − E x 1 ) + Cov ( y , x ~ 2 ) D x ~ 2 ( x ~ 2 − E x ~ 2 ) = ⋯ + Cov ( y , x 2 ) − Cov ( y , x ^ 2 ) D x ~ 2 ( x 2 − x ^ 2 ) = ⋯ + C y x 2 − C x 1 x 2 C y x 1 D x 1 D x 2 − C x 1 x 2 2 D x 1 ( x 2 − E 2 − Cov ( x 2 , x 1 ) D x 1 ( x 1 − E 1 ) ) = ⋯ + C y x 2 D x 1 − C x 1 x 2 C y x 1 D x 1 D x 2 − C x 1 x 2 2 ( x 2 − E 2 − C x 1 x 2 D x 1 ( x 1 − E 1 ) ) = E y + A ( x 1 − E x 1 ) + B ( x 2 − E 2 ) \begin{aligned} \text{E}(y|x_1,x_2) &= \text{E}y +\frac{\left[\begin{matrix} C_{yx_1} & C_{yx_2} \end{matrix}\right]} {\text{D}x_1\text{D}x_2-C^2_{x_1x_2}} \left[\begin{matrix} \text{D}x_2 & -C_{x_1x_2} \\ -C_{x_1x_2} & \text{D}x_1 \end{matrix}\right] \left[\begin{matrix} x_1-\text{E}x_1 \\ x_2-\text{E}x_2 \end{matrix}\right] \\ \text{Cov}(y,\hat{x}_2) &= \text{E}[y\left(\text{E}x_2 +\frac{\text{Cov}(x_2,x_1)}{\text{D}x_1}(x_1-\text{E}x_1)\right)] -\text{E}y\text{E}\hat{x}_2 \\ &= \text{E}y\text{E}x_2+\frac{\text{Cov}(x_2,x_1)}{\text{D}x_1} (\text{E}x_1y-\text{E}x_1\text{E}y)-\text{E}y\text{E}x_2 \\ &= \frac{C_{x_1x_2}C_{yx_1}}{\text{D}x_1} \\ \text{Cov}(x_2,\hat{x}_2) &= \text{E}x_2\hat{x}_2-\text{E}x_2\text{E}\hat{x}_2 \\ &= \text{E}[x_2(\text{E}x_2+\frac{\text{Cov}(x_2,x_1)}{\text{D}x_1} (x_1-\text{E}x_1))]-(\text{E}x_2)^2 \\ &= \frac{C_{x_1x_2}^2}{\text{D}x_1} \\ \text{D}\hat{x}_2 &= \text{D}(\text{E}x_2+\frac{\text{Cov}(x_2,x_1)}{\text{D}x_1} (x_1-\text{E}x_1)) \\ &= \frac{C_{x_1x_2}^2}{(\text{D}x_1)^2}\text{D}x_1 =\frac{C_{x_1x_2}^2}{\text{D}x_1} \\ \text{D}\widetilde{x}_2 &= \text{D}x_2+\text{D}\hat{x}_2 -2\text{Cov}(x_2,\hat{x}_2) \\ &= \text{D}x_2-\frac{C_{x_1x_2}^2}{\text{D}x_1} \\ \text{E}[y|x_1]+\text{E}[y|\widetilde{x}_2]-\text{E}y &= \text{E}y +\frac{C_{x_1y}}{\text{D}x_1}(x_1-\text{E}x_1) +\frac{\text{Cov}(y,\widetilde{x}_2)}{\text{D}\widetilde{x}_2} (\widetilde{x}_2-\text{E}\widetilde{x}_2) \\ &= \cdots+\frac{\text{Cov}(y,x_2)-\text{Cov}(y,\hat{x}_2)}{\text{D}\widetilde{x}_2} (x_2-\hat{x}_2) \\ &= \cdots+\frac{C_{yx_2}-\frac{C_{x_1x_2}C_{yx_1}}{\text{D}x_1}} {\text{D}x_2-\frac{C_{x_1x_2}^2}{\text{D}x_1}}(x_2-\text{E}_2 -\frac{\text{Cov}(x_2,x_1)}{\text{D}x_1}(x_1-\text{E}_1)) \\ &= \cdots+\frac{C_{yx_2}\text{D}x_1-C_{x_1x_2}C_{yx_1}} {\text{D}x_1\text{D}x_2-C_{x_1x_2}^2}(x_2-\text{E}_2 -\frac{C_{x_1x_2}}{\text{D}x_1}(x_1-\text{E}_1)) \\ &= \text{E}y+A(x_1-\text{E}x_1) +B(x_2-\text{E}_2) \\ \end{aligned} E(y∣x1,x2)Cov(y,x^2)Cov(x2,x^2)Dx^2Dx2E[y∣x1]+E[y∣x2]−Ey=Ey+Dx1Dx2−Cx1x22[Cyx1Cyx2][Dx2−Cx1x2−Cx1x2Dx1][x1−Ex1x2−Ex2]=E[y(Ex2+Dx1Cov(x2,x1)(x1−Ex1))]−EyEx^2=EyEx2+Dx1Cov(x2,x1)(Ex1y−Ex1Ey)−EyEx2=Dx1Cx1x2Cyx1=Ex2x^2−Ex2Ex^2=E[x2(Ex2+Dx1Cov(x2,x1)(x1−Ex1))]−(Ex2)2=Dx1Cx1x22=D(Ex2+Dx1Cov(x2,x1)(x1−Ex1))=(Dx1)2Cx1x22Dx1=Dx1Cx1x22=Dx2+Dx^2−2Cov(x2,x^2)=Dx2−Dx1Cx1x22=Ey+Dx1Cx1y(x1−Ex1)+Dx2Cov(y,x2)(x2−Ex2)=⋯+Dx2Cov(y,x2)−Cov(y,x^2)(x2−x^2)=⋯+Dx2−Dx1Cx1x22Cyx2−Dx1Cx1x2Cyx1(x2−E2−Dx1Cov(x2,x1)(x1−E1))=⋯+Dx1Dx2−Cx1x22Cyx2Dx1−Cx1x2Cyx1(x2−E2−Dx1Cx1x2(x1−E1))=Ey+A(x1−Ex1)+B(x2−E2)
among
B = C y x 2 D x 1 − C x 1 x 2 C y x 1 D x 1 D x 2 − C x 1 x 2 2 A = C x 1 y D x 1 − B C x 1 x 2 D x 1 \begin{aligned} B &= \frac{C_{yx_2}\text{D}x_1-C_{x_1x_2}C_{yx_1}} {\text{D}x_1\text{D}x_2-C_{x_1x_2}^2} \\ A &= \frac{C_{x_1y}}{\text{D}x_1}-B\frac{C_{x_1x_2}}{\text{D}x_1} \end{aligned} BA=Dx1Dx2−Cx1x22Cyx2Dx1−Cx1x2Cyx1=Dx1Cx1y−BDx1Cx1x2
In another equation E ( y ∣ x 1 , x 2 ) \text{E}(y|x_1,x_2) E(y∣x1,x2) in ,
A = C y x 1 D x 2 − C y x 2 C x 1 x 2 D x 1 D x 2 − C x 1 x 2 2 B = C y x 2 D x 1 − C y x 1 C x 1 x 2 D x 1 D x 2 − C x 1 x 2 2 \begin{aligned} A &= \frac{C_{yx_1}\text{D}x_2-C_{yx_2}C_{x_1x_2}} {\text{D}x_1\text{D}x_2-C^2_{x_1x_2}} \\ B &= \frac{C_{yx_2}\text{D}x_1-C_{yx_1}C_{x_1x_2}} {\text{D}x_1\text{D}x_2-C^2_{x_1x_2}} \\ \end{aligned} AB=Dx1Dx2−Cx1x22Cyx1Dx2−Cyx2Cx1x2=Dx1Dx2−Cx1x22Cyx2Dx1−Cyx1Cx1x2
The two expressions are equal .
DC level in Gaussian white noise
This example can be used as a cushion , It is helpful to understand the source of each formula of Kalman filter , such as x ( k ) x(k) x(k) and x ( k − 1 ) x(k-1) x(k−1) Why should there be a x ^ ( k ∣ k − 1 ) \hat{x}(k|k-1) x^(k∣k−1) etc. . Consider the model
x ( k ) = A + w ( k ) x(k)=A+w(k) x(k)=A+w(k)
among A A A Is the parameter to be estimated , w ( k ) w(k) w(k) Yes, the mean is 0、 The variance of σ 2 \sigma^2 σ2 The Gaussian white noise of , x ( k ) x(k) x(k) It's observation . You can get x ^ ( 0 ) = x ( 0 ) \hat{x}(0)=x(0) x^(0)=x(0), And then according to x ( 0 ) x(0) x(0) and x ( 1 ) x(1) x(1) forecast k = 1 k=1 k=1 The value of the moment E [ x ( 1 ) ∣ x ( 1 ) , x ( 0 ) ] \text{E}[x(1)|x(1),x(0)] E[x(1)∣x(1),x(0)] when , Conditional additivity of the joint normal distribution is required , But because of x ( 1 ) x(1) x(1) and x ( 0 ) x(0) x(0) Not independent , You need to use the projection theorem to calculate two independent variables x ( 0 ) x(0) x(0) And x ~ ( 1 ∣ 0 ) \widetilde{x}(1|0) x(1∣0), And then calculate x ^ ( 1 ) \hat{x}(1) x^(1), namely
x ^ ( 1 ) = E [ x ( 1 ) ∣ x ( 1 ) , x ( 0 ) ] = E [ x ( 1 ) ∣ x ( 0 ) , x ~ ( 1 ∣ 0 ) ] = E [ x ( 1 ) ∣ x ( 0 ) ] + E [ x ( 1 ) ∣ x ~ ( 1 ∣ 0 ) ] − E x ( 1 ) \begin{aligned} \hat{x}(1) &= \text{E}[x(1)|x(1),x(0)] \\ &= \text{E}[x(1)|x(0),\widetilde{x}(1|0)] \\ &= \text{E}[x(1)|x(0)]+\text{E}[x(1)|\widetilde{x}(1|0)]-\text{E}x(1) \end{aligned} x^(1)=E[x(1)∣x(1),x(0)]=E[x(1)∣x(0),x(1∣0)]=E[x(1)∣x(0)]+E[x(1)∣x(1∣0)]−Ex(1)
among E [ x ( 1 ) ∣ x ( 0 ) ] = x ^ ( 1 ∣ 0 ) \text{E}[x(1)|x(0)]=\hat{x}(1|0) E[x(1)∣x(0)]=x^(1∣0),
x ^ ( 1 ∣ 0 ) = E x ( 1 ) + Cov ( x ( 1 ) , x ( 0 ) ) D x ( 0 ) ( x ( 0 ) − E x ( 0 ) ) = A + E ( A + w ( 1 ) ) ( A + w ( 0 ) ) − E ( A + w ( 1 ) ) E ( A + w ( 0 ) ) E ( A + w ( 1 ) ) 2 − [ E ( A + w ( 1 ) ) ] 2 ( x ( 0 ) − A ) = A \begin{aligned} \hat{x}(1|0) &= \text{E}x(1)+\frac{\text{Cov}(x(1),x(0))} {\text{D}x(0)}(x(0)-\text{E}x(0)) \\ &= A+\frac{\text{E}(A+w(1))(A+w(0))-\text{E}(A+w(1))\text{E}(A+w(0))} {\text{E}(A+w(1))^2-[\text{E}(A+w(1))]^2}(x(0)-A) \\ &= A \end{aligned} x^(1∣0)=Ex(1)+Dx(0)Cov(x(1),x(0))(x(0)−Ex(0))=A+E(A+w(1))2−[E(A+w(1))]2E(A+w(1))(A+w(0))−E(A+w(1))E(A+w(0))(x(0)−A)=A
In this case, there appears x ^ ( k ∣ k − 1 ) \hat{x}(k|k-1) x^(k∣k−1), And another unknown formula E [ x ( 1 ) ∣ x ~ ( 1 ∣ 0 ) ] \text{E}[x(1)|\widetilde{x}(1|0)] E[x(1)∣x(1∣0)]. Apply the theorem from zero mean ,
E [ x ( 1 ) ∣ x ~ ( 1 ∣ 0 ) ] = E x ( 0 ) + Cov ( x ( 1 ) , x ~ ( 1 ∣ 0 ) ) D x ~ ( 1 ∣ 0 ) ( x ~ ( 1 ∣ 0 ) − E x ~ ( 1 ∣ 0 ) ) \text{E}[x(1)|\widetilde{x}(1|0)] = \text{E}x(0)+\frac{\text{Cov}(x(1),\widetilde{x}(1|0))} {\text{D}\widetilde{x}(1|0)}(\widetilde{x}(1|0)-\text{E}\widetilde{x}(1|0)) E[x(1)∣x(1∣0)]=Ex(0)+Dx(1∣0)Cov(x(1),x(1∣0))(x(1∣0)−Ex(1∣0))
among
x ~ ( 1 ∣ 0 ) = x ( 1 ) − x ^ ( 1 ∣ 0 ) E x ~ ( 1 ∣ 0 ) = E ( x − x ^ ) = 0 D x ~ ( 1 ∣ 0 ) = E ( x ( 1 ) − x ^ ( 1 ∣ 0 ) ) 2 = E ( A + w ( 1 ) ) 2 = a 2 P ( 0 ) + σ 2 = P ( 1 ∣ 0 ) \begin{aligned} \widetilde{x}(1|0) &= x(1)-\hat{x}(1|0) \\ \text{E}\widetilde{x}(1|0) &= \text{E}(x-\hat{x}) = 0 \\ \text{D}\widetilde{x}(1|0) &= \text{E}(x(1)-\hat{x}(1|0))^2 \\ &= \text{E}(A+w(1))^2 \\ &= a^2P(0)+\sigma^2 \\ &= P(1|0) \end{aligned} x(1∣0)Ex(1∣0)Dx(1∣0)=x(1)−x^(1∣0)=E(x−x^)=0=E(x(1)−x^(1∣0))2=E(A+w(1))2=a2P(0)+σ2=P(1∣0)
Kalman filter is formally derived
Scalar form
x ^ ( k ∣ k − 1 ) = E [ x ( k ) ∣ Y ( k − 1 ) ] = E [ a x ( k − 1 ) + b u ( k − 1 ) + v ( k − 1 ) ∣ Y ( k − 1 ) ] = a E [ x ( k − 1 ) ∣ Y ( k − 1 ) ] + b E [ u ( k − 1 ) ∣ Y ( k − 1 ) ] + E [ v ( k − 1 ) ∣ Y ( k − 1 ) ] = a x ^ ( k − 1 ) + b u ( k − 1 ) x ~ ( k ∣ k − 1 ) = x ( k ) − x ^ ( k ∣ k − 1 ) = ( a x ( k − 1 ) + b u ( k − 1 ) + v ( k − 1 ) ) − ( a x ^ ( k − 1 ) + b u ( k − 1 ) ) = a x ~ ( k − 1 ) + v ( k − 1 ) (1) \begin{aligned} \hat{x}(k|k-1) &= \text{E}[x(k)|Y(k-1)] \\ &= \text{E}[ax(k-1)+bu(k-1)+v(k-1)|Y(k-1)] \\ &= a\text{E}[x(k-1)|Y(k-1)]+b\text{E}[u(k-1)|Y(k-1)]+\text{E}[v(k-1)|Y(k-1)] \\ &= a\hat{x}(k-1)+bu(k-1) \\ \widetilde{x}(k|k-1) &= x(k)-\hat{x}(k|k-1) \\ &= (ax(k-1)+bu(k-1)+v(k-1))-(a\hat{x}(k-1)+bu(k-1)) \\ &= a\widetilde{x}(k-1)+v(k-1) \end{aligned} \tag{1} x^(k∣k−1)x(k∣k−1)=E[x(k)∣Y(k−1)]=E[ax(k−1)+bu(k−1)+v(k−1)∣Y(k−1)]=aE[x(k−1)∣Y(k−1)]+bE[u(k−1)∣Y(k−1)]+E[v(k−1)∣Y(k−1)]=ax^(k−1)+bu(k−1)=x(k)−x^(k∣k−1)=(ax(k−1)+bu(k−1)+v(k−1))−(ax^(k−1)+bu(k−1))=ax(k−1)+v(k−1)(1)
It is known that x ^ ( k ) = E [ x ( k ) ∣ Y ( k ) ] \hat{x}(k)=\text{E}[x(k)|Y(k)] x^(k)=E[x(k)∣Y(k)], And because x ~ ( k − 1 ) \widetilde{x}(k-1) x(k−1) contain x ( k ) x(k) x(k), x ( k ) x(k) x(k) Contain, y ( k ) y(k) y(k), So the dataset Y ( k ) Y(k) Y(k) Equivalent to data set Y ( k − 1 ) Y(k-1) Y(k−1)、 x ~ ( k ∣ k − 1 ) \widetilde{x}(k|k-1) x(k∣k−1), So by conditional additivity ,
x ^ ( k ) = E [ x ( k ) ∣ Y ( k − 1 ) , x ~ ( k − 1 ) ] = E [ x ( k ) ∣ Y ( k − 1 ) ] + E [ x ( k ) ∣ x ~ ( k ∣ k − 1 ) ] − E x ( k ) = x ^ ( k ∣ k − 1 ) + E [ x ( k ) ∣ x ~ ( k ∣ k − 1 ) ] − E x ( k ) \begin{aligned} \hat{x}(k) &= \text{E}[x(k)|Y(k-1),\widetilde{x}(k-1)] \\ &= \text{E}[x(k)|Y(k-1)]+\text{E}[x(k)|\widetilde{x}(k|k-1)]-\text{E}x(k) \\ &= \hat{x}(k|k-1)+\text{E}[x(k)|\widetilde{x}(k|k-1)]-\text{E}x(k) \end{aligned} x^(k)=E[x(k)∣Y(k−1),x(k−1)]=E[x(k)∣Y(k−1)]+E[x(k)∣x(k∣k−1)]−Ex(k)=x^(k∣k−1)+E[x(k)∣x(k∣k−1)]−Ex(k)
Apply the theorem from zero mean ,
E [ x ( k ) ∣ x ~ ( k ∣ k − 1 ) ] = E x ( k ) + Cov ( x ( k ) , x ~ ( k ∣ k − 1 ) ) D x ~ ( k ∣ k − 1 ) ( x ~ ( k ∣ k − 1 ) − E x ~ ( k ∣ k − 1 ) ) \text{E}[x(k)|\widetilde{x}(k|k-1)] = \text{E}x(k)+\frac{\text{Cov}(x(k),\widetilde{x}(k|k-1))} {\text{D}\widetilde{x}(k|k-1)}(\widetilde{x}(k|k-1)-\text{E}\widetilde{x}(k|k-1)) E[x(k)∣x(k∣k−1)]=Ex(k)+Dx(k∣k−1)Cov(x(k),x(k∣k−1))(x(k∣k−1)−Ex(k∣k−1))
among
E x ~ ( k ∣ k − 1 ) = E ( x − x ^ ) = 0 D x ~ ( k ∣ k − 1 ) = E ( a x ~ ( k − 1 ) + v ( k − 1 ) ) 2 = a 2 P ( k − 1 ) + V = P ( k ∣ k − 1 ) (3) \begin{aligned} \text{E}\widetilde{x}(k|k-1) &= \text{E}(x-\hat{x}) = 0 \\ \text{D}\widetilde{x}(k|k-1) &= \text{E}(a\widetilde{x}(k-1)+v(k-1))^2 \\ &= a^2P(k-1)+V \\ &= P(k|k-1) \tag{3} \end{aligned} Ex(k∣k−1)Dx(k∣k−1)=E(x−x^)=0=E(ax(k−1)+v(k−1))2=a2P(k−1)+V=P(k∣k−1)(3)
Make
M ( k ) = Cov ( x ( k ) , x ~ ( k ∣ k − 1 ) ) D x ~ ( k ∣ k − 1 ) M(k)=\frac{\text{Cov}(x(k),\widetilde{x}(k|k-1))} {\text{D}\widetilde{x}(k|k-1)} M(k)=Dx(k∣k−1)Cov(x(k),x(k∣k−1))
be
E [ x ( k ) ∣ x ~ ( k ∣ k − 1 ) ] = E x ( k ) + M ( k ) ( x ( k ) − x ^ ( k ∣ k − 1 ) ) x ^ ( k ) = E [ x ( k ) ∣ Y ( k − 1 ) , x ~ ( k − 1 ) ] = E [ x ( k ) ∣ Y ( k − 1 ) ] + E [ x ( k ) ∣ x ~ ( k ∣ k − 1 ) ] − E x ( k ) = x ^ ( k ∣ k − 1 ) + M ( k ) ( x ( k ) − x ^ ( k ∣ k − 1 ) ) \begin{aligned} \text{E}[x(k)|\widetilde{x}(k|k-1)] &= \text{E}x(k)+M(k)(x(k)-\hat{x}(k|k-1)) \\ \hat{x}(k) &= \text{E}[x(k)|Y(k-1),\widetilde{x}(k-1)] \\ &= \text{E}[x(k)|Y(k-1)]+\text{E}[x(k)|\widetilde{x}(k|k-1)]-\text{E}x(k) \\ &= \hat{x}(k|k-1)+M(k)(x(k)-\hat{x}(k|k-1)) \end{aligned} E[x(k)∣x(k∣k−1)]x^(k)=Ex(k)+M(k)(x(k)−x^(k∣k−1))=E[x(k)∣Y(k−1),x(k−1)]=E[x(k)∣Y(k−1)]+E[x(k)∣x(k∣k−1)]−Ex(k)=x^(k∣k−1)+M(k)(x(k)−x^(k∣k−1))
By the projection theorem E [ x ^ ( x − x ^ ) ] = 0 \text{E}[\hat{x}(x-\hat{x})]=0 E[x^(x−x^)]=0 Calculation M ( k ) M(k) M(k),
M ( k ) = Cov ( x ( k ) , x ~ ( k ∣ k − 1 ) ) D x ~ ( k ∣ k − 1 ) = E [ x ( k ) ( x ( k ) − x ^ ( k ∣ k − 1 ) ) ] − E x ( k ) E x ~ ( k ∣ k − 1 ) P ( k ∣ k − 1 ) = E [ ( x ( k ) − x ^ ( k ∣ k − 1 ) ) ( x ( k ) − x ^ ( k ∣ k − 1 ) ) ] P ( k ∣ k − 1 ) \begin{aligned} M(k) &= \frac{\text{Cov}(x(k),\widetilde{x}(k|k-1))} {\text{D}\widetilde{x}(k|k-1)} \\ &= \frac{\text{E}[x(k)(x(k)-\hat{x}(k|k-1))] -\text{E}x(k)\text{E}\widetilde{x}(k|k-1)}{P(k|k-1)} \\ &= \frac{\text{E}[(x(k)-\hat{x}(k|k-1))(x(k)-\hat{x}(k|k-1))]}{P(k|k-1)} \\ \end{aligned} M(k)=Dx(k∣k−1)Cov(x(k),x(k∣k−1))=P(k∣k−1)E[x(k)(x(k)−x^(k∣k−1))]−Ex(k)Ex(k∣k−1)=P(k∣k−1)E[(x(k)−x^(k∣k−1))(x(k)−x^(k∣k−1))]
5 The equations are ,
(1) Prediction equation
(2) Correct the equation
(3) Minimum prediction mean square error
Vector form
x ^ ( k ∣ k − 1 ) = E [ x ( k ) ∣ Y ( k − 1 ) ] = E [ A x ( k − 1 ) + B u ( k − 1 ) + v ( k − 1 ) ∣ Y ( k − 1 ) ] = A E [ x ( k − 1 ) ∣ Y ( k − 1 ) ] + B E [ u ( k − 1 ) ∣ Y ( k − 1 ) ] + E [ v ( k − 1 ) ∣ Y ( k − 1 ) ] = A x ^ ( k − 1 ) + B u ( k − 1 ) \begin{aligned} \hat{x}(k|k-1) &= \text{E}[x(k)|Y(k-1)] \\ &= \text{E}[Ax(k-1)+Bu(k-1)+v(k-1)|Y(k-1)] \\ &= A\text{E}[x(k-1)|Y(k-1)]+B\text{E}[u(k-1)|Y(k-1)]+\text{E}[v(k-1)|Y(k-1)] \\ &= A\hat{x}(k-1)+Bu(k-1) \\ \end{aligned} x^(k∣k−1)=E[x(k)∣Y(k−1)]=E[Ax(k−1)+Bu(k−1)+v(k−1)∣Y(k−1)]=AE[x(k−1)∣Y(k−1)]+BE[u(k−1)∣Y(k−1)]+E[v(k−1)∣Y(k−1)]=Ax^(k−1)+Bu(k−1)
Reference resources
- Sunzengqi . Computer control theory and application [M]. tsinghua university press , 2008.
- StevenM.Kay, Luopengfei . Fundamentals of statistical signal processing [M]. Electronic industry press , 2014.
- Zhaoshujie , Jian-xun zhao . Signal detection and estimation theory [M]. Electronic industry press , 2013.
- The derivation process of Kalman filter is explained in detail
边栏推荐
- ASCII码对照表
- File upload vulnerability - simple exploitation 2 (Mozhe college shooting range)
- Capriccio in the Internet Age
- Implement AOP and interface caching on WPF client
- Solution to unlimited restart of desktop and file explorer
- New product release: domestic single port Gigabit network card is officially mass produced!
- 产品资讯|PoE网卡家族集体亮相,机器视觉完美搭档!
- [data visualization] Apache superset 1.2.0 tutorial (II) - Quick Start (visualizing King hero data)
- 【博弈论-绪论】
- One article to show you how to understand the harmonyos application on the shelves
猜你喜欢

The scale of the global machine vision market continues to rise. Poe image acquisition card provides a high-speed transmission channel for industrial cameras

ORA-04098: trigger ‘xxx. xxx‘ is invalid and failed re-validation

New product release: domestic single port Gigabit network card is officially mass produced!

Part II data link layer

Online excel file parsing and conversion to JSON format
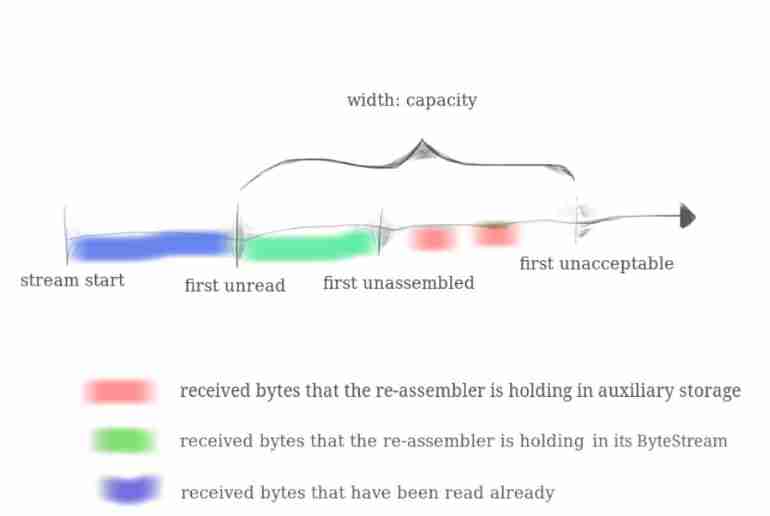
Cs144 lab0 lab1 record

php pcntl_ Fork create multiple child process resolution

JVM方法区

第一部分 物理层

新品发布:LR-LINK联瑞推出首款25G OCP 3.0 网卡
随机推荐
ORA-04098: trigger ‘xxx. xxx‘ is invalid and failed re-validation
Space transcriptome experiment | what factors will affect the quality of space transcriptome sequencing during the preparation of clinical tissue samples?
JVM object allocation policy TLAB
正则校验匹配[0-100]、[0-1000]之间的正整数或小数点位数限制
Brain cell membrane equivalent neural network training code
Goto statement of go language
UI automated interview questions
银泰百货与淘宝天猫联合打造绿色潮玩展,助力“碳中和”
Lr-link Lianrui makes its debut at the digital Expo with new products - helping the construction of new infrastructure data center
Live broadcast with practice | 30 minutes to build WordPress website with Alibaba cloud container service and container network file system
How to Load Data from CSV (Data Preparation Part)
Toolbar替换ActionBar后Title不显示
How to manually drag nodes in the Obsidian relationship graph
全球机器视觉市场规模持续上涨,PoE图像采集卡为工业相机提供高速传输通道
电竞网咖用2.5G网卡,体验飞一般的感觉!
关于gorm的preload方法笔记说明
Vectordrawable error
Solve the problem of img 5px spacing
In idea, run the yarn command to show that the file cannot be loaded because running scripts is disabled on this system
Log in with password and exit with error for three times.