leetcode：153. 寻找旋转排序数组中的最小值

题目来源

• 153. 寻找旋转排序数组中的最小值

题目描述

题目解析

为了便于分析，我们先将数组中的数画在二维坐标系中，横坐标表示数组下标，纵坐标表示数组数值，如下所示：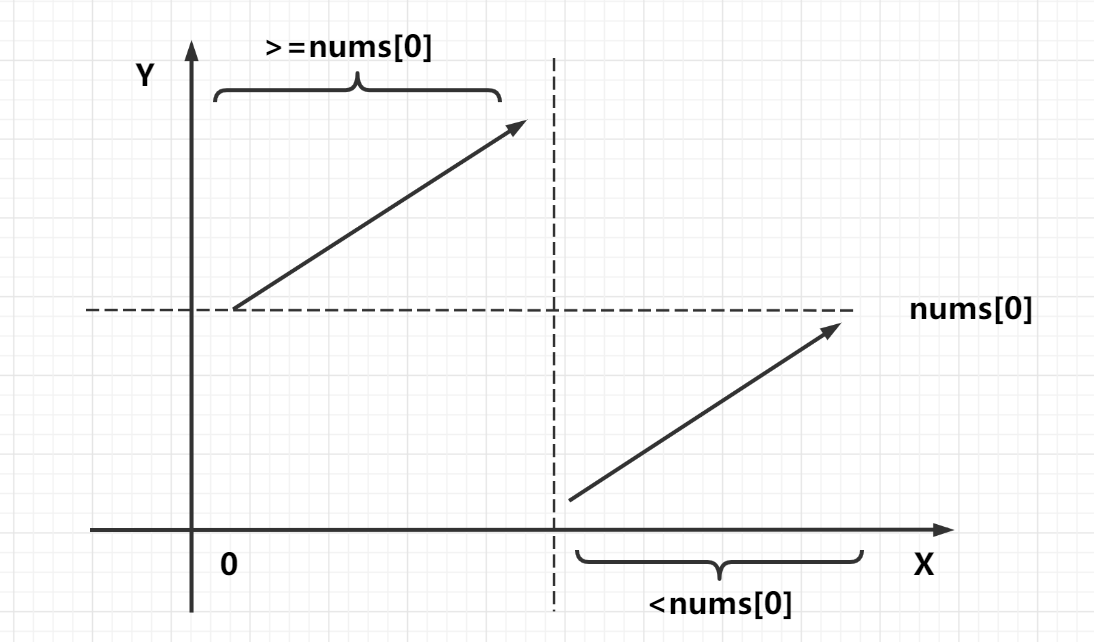

我们发现：竖直虚线左边的数满足 nums[i]≥nums[0]，而竖直虚线右边的数满足nums[i]< nums[0]，分界点就是整个数组的最小值。数组具有二分性，所以我们可以二分出最小值的位置。

算法：

• 在[l,r]区间中， l = 0, r = nums.size() - 1，我们去二分<num[0]的最左边界。
• 当nums[mid] < nums[0]时，往左边区域找，r = mid。
• 当nums[mid] >= nums[0]时，往右边区域找，l = mid + 1。
• 当二分的范围缩小至一个数时，就是最小值的位置。

class Solution {
    
public:
    int findMin(vector<int>& nums) {
    
        int l = 0, r = nums.size() - 1;
        if(nums[r] > nums[l]) return nums[0];  //升序数组，数组完全单调，第一个数最小
        while(l < r)
        {
    
            int mid = (l + r)/2;
            if(nums[mid] < nums[0])  r = mid;
            else l = mid + 1;
        }
        return nums[r];
    }
};

思路

class Solution {
    
public:
    // 思路跟翻转数组一样，等分后的数组一定有一个是有序的，有序的数组取最左数为min，接着对之后的数组进行同样的操作。
    int findMin(vector<int>& nums) {
    
        int minVal = INT32_MAX;
        int l = 0, r = nums.size() - 1;
        while (l <= r) {
    
            int m = l + (r - l) / 2;
            int lv = nums[l], mv = nums[m], rv = nums[r];

            if (lv == mv) {
     // 只有2个数了, 初始1个也在其中
                minVal = min(minVal, min(lv, rv));
                break;
            }
            if (lv < mv) {
     // 左半边有序
                minVal = min(minVal, lv);
                l = m + 1;
            } else {
     // 右半边有序
                minVal = min(minVal, mv);
                r = m - 1;
            }
        }
        return minVal;
    }
};

class Solution {
    
public:

    int findMin(vector<int>& nums) {
    
        int min = nums[0];
        int left = 0, right = nums.size() -1;
        while (left<=right){
    
            int mid = (right-left)/2+left;
            if (nums[mid]<nums[right]){
    
                right = mid-1;
            }else {
    
                left = mid+1;
            }
            if (nums[mid]<min) 
                min = nums[mid];
        }
        return min;
    }
};

思路：

只有三种情况

• 1.中间值大于两端，则说明最小值在右侧
• 2.中间值小于两端，则说明最小值在左侧
• 3.中间值介于两者之间，则说明此时已按顺序排列，最小值就是L

当LR相邻的时候就可以break了，此时LR中必定有一个是最小值