动态规划 --- 状态压缩DP 详细解释

蒙德里安的梦想

把一个 N × M 的棋盘分成若干个 1 × 2 的小长方形，问：一共有多少种方案？例如当 N = 2，M = 4（两行、四列），一共有 5 种分割方案

题目给出一个 N × M 的矩形，问我们把一个 N × M 的矩形切成若干个 1 × 2 的小长方形，一共有多少种不同的切法？

这道题目其实是状态压缩的经典应用，把问题转换为往矩形里面放 1 × 2 的小方格，可以横着放也可以竖着放，问：一共有多少种不同的放法？

当我们把所有横向小方格放完的时候，纵向小方格一定只有一种情况放进去，没有其他选择，只能一列一列放进去

所以整个的划分方式与横向小方格的摆放方案数是相等的，当我们把所有横向小方格摆好的时候，纵向小方格就只能顺次摆好，只有一种方案，所以：

核心

整个摆放 1 × 2 小方格的方案数量是等于摆放 1 × 2 小方格的方案数

接下来看一下怎么求横向摆放小方格的方案数？

这个我们可以一列一列来求，每一列用一个状态f[ i ][ j ]来表示，f[ i ][ j ] 表示现在要摆放第 i 列，1 × 2 的小方格每一列摆放的时候只会与上一列有关系，上一列伸出来的小方格的状态是 j 的情况下，把上一列伸出来的小方格的那些行的状态放到 j 里面去，j 实际上是一个二进制数，一共有 5 行，j 是一个五位的二进制数，所以 j 的范围是从 0 ~ 31，j 存储的其实是上一列当中哪些列伸出来了躺着的 1 × 2 的小方格，例如 i 在第二列的时候，让我们看看它前面一列 j 的状态吧，第一行伸出来是 1，第二行没有伸出来是 0，第三行没有伸出来是 0，第四行伸出来是 1，第五行没有伸出来是 0，这种状态表示的是 k = 10010，也就是说，f[ i ][ j ] 表示的是所有摆到第 i 列，上一列伸出来的小方格的行的状态是 j 的情况下，它总共的方案数

那么 f[ i ][ j ] 怎么转移呢？

我们来枚举一下第 i - 1 列的所有状态，比方说，我们现在要计算第 i 列的某一个状态，然后我们枚举一下第 i - 1 列的某一个状态，例如我们当前要计算的状态是 j = 00001，然后我们要枚举上一个状态，如下图所示

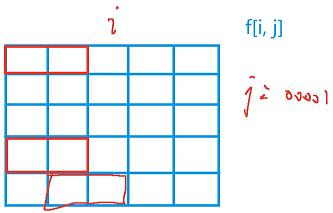
我们枚举的上一个状态是 k，k = 10010【也就是第 i - 1 列的所有状态】

然后要判断一下这个状态能否转移过来，它能转移过来的第一个条件是 j 和 k 不能有冲突：在第 i - 1 列来说，从第 i - 1 列伸到第 i 列的行，和从第 i - 2 列伸到第 i -  1 列的行不能冲突，否则就会发生矛盾，解决这个问题我们可以用位运算来判断，j & k ？= 0

第二个条件是剩余的这些列【第 i - 1 列这些剩余的空白格子】，所有连续的空白格子的长度必须是偶数，由于只枚举横向摆放的格子，第 i - 1 列已经枚举完了，剩余的格子必须要用纵向的格子来填充，但是纵向小方块的长度是 2，所以不能填长度是奇数这样的连续一段，只能填长度是偶数这样的连续一段，所以我们的第二个条件是 j | k，j | k 所有 0 的位置就是现在第 i - 1 列现在空白的小方块，j | k 这一段里面不能存在连续奇数个 0

只要满足以上两个条件就可以转移过来，可以对应到一种方案，f(i，j) += f(i - 1，k)，判断 k 是不是满足条件就可以了，把所有满足条件的 k 加进来就可以了，j | k 这一段不存在连续奇数个 0 可以先预处理出来

时间复杂度分析

11 × (状态数量) × (转移的数量，也就是每一个状态计算需要枚举的数量) = 4 ×

难点

状态压缩的状态虽然是一个整数，但是我们要把它看成一个二进制数，二进制数里面的每一位是 0 是 1 表示不同的情况

以下内容参考

运算符和表达式

蒙德里安的梦想   AcWing 291 蒙德里安的梦想（详细注释 ）

a&&b：a和b都成立它才能成立，其他情况都是不成立，都为 1 才为 1

   a||b：a和b都不成立它才能不成立，其他情况都是成立，都为 0 才为 0

可能遇到的问题汇总

st[j | k] 表示的是第 i - 1 列是否合法，即该列所有连续的 0 是否都为偶数

st[x]，代表某一列当前的状态是x, 比如x=， 这就是一个合法状态，所以它不是某一列的值，而是看一种摆放方法是不是合法
1. 其中 j 表示第 i - 1 列伸到第 i 列的状态，k 表示第 i - 2 列伸到第 i - 1 列的状态 （注意此时某位置为 0 并不代表当前位置没有方块，只代表没有从上一列伸过来的方块）
2. j | k 表示的就是第 i - 1 列被方块填充的状态（1代表当前位置有方块，0 代表当前位置无方块）

3. j | k 的实际表示的是第 i - 1 列合并列后的位置表示，之前的 st 数组预处理作用是记录 i = 1 ~ 1 << n 中能够满足连续0的个数为偶数的 i，st[ j | k ] = true 就意味着此时第 i - 1 列只存在连续偶数个 0，也就意味着不存在连续奇数个 0

4.if(cnt &1) st[ i ] = false；最下面的那一段判断一下连续 0 的个数，这是什么的最后一段？

    回答：此列有突出的一行为1，没有突出的为0。比如 00000 因为只有循环到 1 时候才会将 st[ i ] 置为false，break跳出循环，当循环结束时，此时没有1，所以 st[ i ] 仍为true，但是显然有相邻的奇数个0，这时就体现出if(cnt &1) st[ i ] = false；的作用了

5.为什么要 memset(f，0，sizeof f)；和 st[ i ] = true；呢？  上次循环中对这次 st 操作有什么影响吗？还有 f 数组初始值不是本来就是 0 吗？

    回答：输入的是多组样例，防止上一组测试数据的遗留对本组数据造成影响。

6.为什么f[0][0]，空棋盘的时候方案数是1？

    回答：初始时第0列左边是空的，所以不会有任何一个小方块伸出来，所以f[0][0]所表示的是一个合法状态，所以初值是1。

7.为什么状态k和状态j不能有交集？

    回答：第 i-2 伸到第 i-1 列的状态为 j
               第 i-1 伸到第 i 列的状态为 k
1×2的小方块，已经在i-2列的某一行放置了，那么第i-1对应的行就没法放，因为小方块为1×2，第i-1列对应行的那个位置被占据了。 因为不能有交集，才能合法地从放f(i -1，k)状态转移到f(i，j)状态

#include <iostream>
#include <algorithm>
//memset头文件
#include <string>

using namespace std;
//数据范围1~11
const int N = 12;
//每一列的每一个空格有放和不放两种选择 所以是2^n
const int M = 1 << N;

/* 
    状态转移方程:第一维表示列,第二维表示所有可能的状态
    方案数比较大,所以要使用long long 类型
    f[i][j]表示前i-1列的方案数已经确定,且从i-1列伸出,并且第i列的状态是j的所有方案数
*/
long long f[N][M];

/*
    表示当前方案是不是合法情况,存储每种状态有多少个连续的0
    如果是奇数个0置为false表示无效状态,如果是偶数个0置为true表示能成功转移
*/
bool st[M];

//n、m表示矩形的行数、列数
int n, m;

int main()
{
    int n, m;
    //读入n和m 输入不是两个0就表示合法输入需要继续读入
    while(cin >> n >> m, n || m)
    {
        /* 预处理st数组 */
        //预处理所有状态是不是不存在连续奇数个0
        for(int i = 0; i < 1 << n; i++ )
        {
            /*
                一开始置为true表示偶数个0假定能成功转移到 
                第i-2列伸到i-1列的状态为k
                第i-1列伸到i列的状态为j
            */
            st[i] = true;
            //cnt记录当前这一列连续0的个数
            int cnt = 0;
            //遍历这一列 从上到下
            for(int j = 0; j < n;j++ )
                /*
                    通过位运算表示i状态下的第j位是否放置方格
                    0表示不放 1表示放
                    i >> j位运算 表示i（i在此处是一种状态）的二进制数的第j位
                    &1为判断该位是否为1 如果为1进入if
                */
                if(i >> j & 1)
                {
                    /*
                        如果当前这一位是1说明上一段已经截止了
                        需要判断上一段连续的0是不是有奇数个,如果有奇数个说明第i个状态是不合法的
                    */
                    if(cnt & 1) st[i] = false;
                    //把cnt置为0 表示连续一段结束
                    cnt = 0;
                } 
                else 
                    /*
                        否则的话该位还是0 统计连续0的计数器++
                    */
                    cnt++;
            //如果最后一段连续0的个数是奇数 把st置为false
            if(cnt & 1) st[i] = false;
        }
        /* dp过程 */
        //初始化状态数组f
        memset(f, 0, sizeof f);
        /* 
            棋盘是从第0列开始,没有第-1列,所以第0列第0行不会有延伸出来的小方块
            没有横着摆放的小方块,所有小方块都是竖着摆放的,这种状态记录为一种方案
        */
        f[0][0] = 1;
        //枚举所有列 n、m表示矩形的行数、列数
        for(int i = 1;i <= m;i++ )
            //枚举第i列的所有的状态
            for(int j = 0;j < 1 << n;j++ )
                //枚举第i-1列的所有状态
                for(int k = 0;k < 1 << n;k++ )
                    //判断两个条件
                    if((j & k) == 0 && st[j | k])
                        f[i][j] += f[i - 1][k];
        /*
            棋盘一共有0~m-1列
            f[i][j]表示前i-1列的方案数已经确定,从i-1列伸出,并且第i列的状态是j的所有方案数
            f[m][0]表示前m-1列的方案数已经确定,从m-1列伸出,并且第m列的状态是0的所有方案数
            也就是m列不放小方格,前m-1列已经完全摆放好并且不伸出来的状态
        */    
        cout << f[m][0] << endl;
    }
    return 0;
}