当前位置:网站首页>(部分不懂,笔记整理未完成)【图论】差分约束
(部分不懂,笔记整理未完成)【图论】差分约束
2022-08-02 06:01:00 【gzkeylucky】
知识点
一. 前置知识:判断负环
二.差分约束
差分约束系统即为n元一次不等式组,每个约束条件都是由两个变量作差构成的,形如 ,目标为求出一组解可以满足所有约束条件。
,目标为求出一组解可以满足所有约束条件。
 可变形为
可变形为 ,与最短路中三角形不等式
,与最短路中三角形不等式 ![dis[y] \leqslant dis[x]+v](http://img.inotgo.com/imagesLocal/202208/02/202208020601064621_6.gif) 相似,于是将不等式组中的变量看作点,每个约束条件
相似,于是将不等式组中的变量看作点,每个约束条件 为从节点 j 向节点 i 连一条边权为
为从节点 j 向节点 i 连一条边权为  的有向边,在跑完最短路后,
的有向边,在跑完最短路后,![x_i=dis[i]](http://img.inotgo.com/imagesLocal/202205/05/202205050512304328_2.gif) 为差分约束系统中的一组解,若存在负环和终点不可达时,无解。
为差分约束系统中的一组解,若存在负环和终点不可达时,无解。
 变形为
变形为  ;
;
 变形为
变形为  ;
;
 变形为
变形为  ;
;
 变形为
变形为  且
且  ;
;
必要时,建一个超级源点。
那么,什么时候需要建立超级原点呢?
有的时候,为了保证整个区间的连通的,就需要建立一个超级源点使得整个图是连通的。但是需要注意的是,在正常建边的时候,如果是从大指向小,这个时候我们建立超级源点的时候就也应该遵循这个原则,如果是是从小指向大的,建立超级源点的时候反过来即可。
!求解最大解用最短路,求解最小解用最长路
题目描述
给出一组包含 m 个不等式,有 n 个未知数的形如:

的不等式组,求任意一组满足这个不等式组的解。
输入格式
第一行为两个正整数 n,m,代表未知数的数量和不等式的数量。
接下来 m 行,每行包含三个整数 c,c′,y,代表一个不等式  。
。
输出格式
一行,n 个数,表示 的一组可行解,如果有多组解,请输出任意一组,无解请输出
的一组可行解,如果有多组解,请输出任意一组,无解请输出 NO。
输入输出样例
输入 #1
3 3 1 2 3 2 3 -2 1 3 1
输出 #1
5 3 5
说明/提示
样例解释

一种可行的方法是 。
。

数据范围
对于 100% 的数据, ,
, ,
, ,
, 。
。
#include <iostream>
#include <cstdio>
#include <cstring>
#include <string>
#include <algorithm>
#include <queue>
using namespace std;
int n,m;
const int maxn=1e7+5,INF=0x3f3f3f3f;
struct node{
int to,next,w;
}edge[maxn<<1];
int head[maxn],num=0,dis[maxn],ans[maxn];
bool vis[maxn];
queue <int> q;
inline int read()
{
int x=0,f=1;
char c=getchar();
while(c<'0'||c>'9')
{
if(c=='-') f=-1;
c=getchar();
}
while(c>='0'&&c<='9')
{
x=(x<<3)+(x<<1)+(c^48);
c=getchar();
}
return x*f;
}
inline void write(int x)
{
if(x<0) putchar('-'),x=-x;
if(x>9) write(x/10);
putchar(x%10+'0');
}
inline void add(int u,int v,int w)
{
edge[++num].to=v;
edge[num].w=w;
edge[num].next=head[u];
head[u]=num;
}
inline bool spfa()
{
memset(dis,INF,sizeof(dis));
memset(ans,0,sizeof(ans));
memset(vis,0,sizeof(vis));
q.push(0); //从超级原点开始
vis[0]=1;
dis[0]=0;
while(!q.empty())
{
int u=q.front();
q.pop();
vis[u]=0;
for(int i=head[u];i!=-1;i=edge[i].next)
{
int v=edge[i].to;
if(dis[v]>dis[u]+edge[i].w)
{
dis[v]=dis[u]+edge[i].w;
ans[v]=ans[u]+1;
if(ans[v] >= n+1)
{
return 1;
}
if(!vis[v])
{
vis[v]=1;
q.push(v);
}
}
}
}
return 0;
}
int main()
{
n=read(); m=read();
memset(head,-1,sizeof(head));
for(int i=1;i<=m;++i)
{
int a=read(),b=read(),y=read();
add(b,a,y); //要注意从b到a,减数放前面
}
for(int i=1;i<=n;++i)
{
add(0,i,0); //构造超级原点
}
if(spfa() == 1) printf("NO\n");
else
{
for(int i=1;i<=n;++i)
{
write(dis[i]);
putchar(' ');
}
}
return 0;
}相关练习
思路:根据题目中的“至多”,“至少”和“一样多”,可以得知以下三条式子:

一般在解决问题的时候,我们希望能将问题转换为一个模型,或者用一个通式来解决大量的问题。
那么在上面三个式子中,①式和②式都为不等式,可以看作是图的有向边。我们希望把两个式子转换成相同的表达方式。那么将②式两边都乘以-1,将式子转换为  ,与①式相似。
,与①式相似。
但是,③式为等式,那么可以看作是图的无向边,除了③式,还可以表示为  ,在代码实现的时候,就像建立无向边一样建立两次。
,在代码实现的时候,就像建立无向边一样建立两次。
为了保证图的联通,我们需要建一个保证联通的超级原点,再从这个超级原点开始跑最短路,最后,注意一定要判断负环!
代码如下:
#include <iostream>
#include <cstdio>
#include <cstring>
#include <string>
#include <algorithm>
#include <queue>
using namespace std;
int n,m;
const int maxn=1e7+5,INF=0x3f3f3f3f;
struct node{
int to,next,w;
}edge[maxn<<1];
int head[maxn],num=0,dis[maxn],ans[maxn];
bool vis[maxn];
queue <int> q;
inline int read()
{
int x=0,f=1;
char c=getchar();
while(c<'0'||c>'9')
{
if(c=='-') f=-1;
c=getchar();
}
while(c>='0'&&c<='9')
{
x=(x<<3)+(x<<1)+(c^48);
c=getchar();
}
return x*f;
}
inline void add(int u,int v,int w)
{
edge[++num].to=v;
edge[num].w=w;
edge[num].next=head[u];
head[u]=num;
}
inline bool spfa()
{
memset(dis,INF,sizeof(dis));
memset(ans,0,sizeof(ans));
memset(vis,0,sizeof(vis));
q.push(0);
vis[0]=1;
dis[0]=0;
while(!q.empty())
{
int u=q.front();
q.pop();
vis[u]=0;
for(int i=head[u];i!=-1;i=edge[i].next)
{
int v=edge[i].to;
if(dis[v]>dis[u]+edge[i].w)
{
dis[v]=dis[u]+edge[i].w;
ans[v]=ans[u]+1;
if(!vis[v])
{
q.push(v);
vis[v]=1;
}
if(ans[v]==n)
{
return 0;
}
}
}
}
return 1;
}
int main()
{
n=read(); m=read();
memset(head,-1,sizeof(head));
for(int i=1;i<=n;++i)
{
add(0,i,0);
}
for(int i=1;i<=m;++i)
{
int num=read();
int a,b,c;
if(num == 1) //a-b<=c的情况
{
a=read(),b=read(),c=read();
add(a,b,-c);
}
else if(num == 2) //a-b >= c的情况
{
a=read(),b=read(),c=read();
add(b,a,c);
}
else
{
a=read(),b=read();
add(a,b,0);
add(b,a,0);
}
}
if(spfa()== 1) printf("Yes");
else printf("No");
return 0;
}2. 洛谷 P1250 种树
方法一:贪心算法
思路:这道题用贪心算法很好理解。为了保证所种的树最少,那么就需要在区间重合的部分种的树越多,然而重叠部分一定在区间的尾部,所以先对区间结束的节点进行排序,然后先依次在区间的头部从前往后种树直到满足要求,对于下一个区间,看看差多少树,就在结尾补多少。
步骤如下:
1. 按结束位置排序
2. 对每个区间进行处理:从前往后扫描区间,统计已有的树的个数
若已选点超过要求个数,则continue;否则从后往前,添加缺少的覆盖点
#include <iostream>
#include <cstdio>
#include <cstring>
#include <string>
#include <algorithm>
#include <queue>
using namespace std;
int n,h,ans=0;
const int maxn=1e7+5;
bool vis[maxn];
struct node{
int b,e,t;
}edge[maxn<<1];
inline int read()
{
int x=0,f=1;
char c=getchar();
while(c<'0'||c>'9')
{
if(c=='-') f=-1;
c=getchar();
}
while(c>='0' && c<='9')
{
x=(x<<3)+(x<<1)+(c^48);
c=getchar();
}
return x*f;
}
inline bool cmp(node x,node y) //根据尾部节点进行排序
{
return x.e<y.e;
}
int main()
{
n=read(); h=read();
for(int i=1;i<=h;++i)
{
edge[i].b=read();
edge[i].e=read();
edge[i].t=read();
}
sort(edge+1,edge+h+1,cmp);
memset(vis,0,sizeof(vis));
for(int i=1;i<=h;++i)
{
int sum=0;
for(int j=edge[i].b;j<=edge[i].e;++j) //从前往后搜索区间
{
if(vis[j]!=0) //区间中存在被标记过的点
{
sum++;
}
}
if(sum >= edge[i].t) continue;
for(int j=edge[i].e;j>=edge[i].b;--j) //从后往前搜索
{
if(vis[j] == 0) //重叠部分增加要种的树
{
vis[j]=1;
sum++; //统计区间的数目增加
ans++; //总数增加
if(sum == edge[i].t) break;
}
}
}
printf("%d",ans);
return 0;
}方法二:差分约束
思路:
根据题意:对于每个约束条件 ,最小值为w ,区间的长度可以表示为
,最小值为w ,区间的长度可以表示为 ,转换成两数之差为
,转换成两数之差为 ,即
,即 ![sum[v]-sum[u-1] \geqslant w](http://img.inotgo.com/imagesLocal/202208/02/202208020601064621_12.gif) ,表示在区间
,表示在区间 ![\left [ u,v \right ]](http://img.inotgo.com/imagesLocal/202207/23/202207230152565330_29.gif) 之间至少有w棵树(sum[x]为x的前缀和)。又因为在每个间隔中只能选择不种或者是种1棵树,得出隐含条件:
之间至少有w棵树(sum[x]为x的前缀和)。又因为在每个间隔中只能选择不种或者是种1棵树,得出隐含条件: ![0 \leqslant sum[v]-sum[v-1] \leqslant 1](http://img.inotgo.com/imagesLocal/202208/02/202208020601064621_26.gif) 。
。
在这道题中还需要注意的一点是:所建立的超级原点为n+1。根据题意,序号为1的位置是可以种树的,如果从0开始建立超级原点,可能会导致序号1的位置只能维持不种树的情况。
#include <iostream>
#include <cstdio>
#include <cstring>
#include <string>
#include <algorithm>
#include <queue>
using namespace std;
int n,h;
const int maxn=1e7+5,INF=0x3f3f3f3f;
struct node
{
int to,next,w;
}edge[maxn<<1];
int head[maxn],num=0,dis[maxn];
struct node1
{
int b,e,t;
}edge1[maxn<<1];
bool vis[maxn];
queue <int> q;
inline int read()
{
int x=0,f=1;
char c=getchar();
while(c<'0'||c>'9')
{
if(c=='-') f=-1;
c=getchar();
}
while(c>='0'&&c<='9')
{
x=(x<<3)+(x<<1)+(c^48);
c=getchar();
}
return x*f;
}
inline void write(int x)
{
if(x<0) putchar('-'),x=-x;
if(x>9) write(x/10);
putchar(x%10+'0');
}
inline void add(int u,int v,int w)
{
edge[++num].to=v;
edge[num].w=w;
edge[num].next=head[u];
head[u]=num;
}
inline bool spfa()
{
memset(dis,INF,sizeof(dis));
q.push(n+1); //从超级原点开始查找
vis[n+1]=1;
dis[n+1]=0;
while(!q.empty())
{
int u=q.front();
q.pop();
vis[u]=0;
for(int i=head[u];i!=-1;i=edge[i].next)
{
int v=edge[i].to;
if(dis[v]>dis[u]+edge[i].w)
{
dis[v]=dis[u]+edge[i].w;
if(!vis[v])
{
q.push(v);
vis[v]=1;
}
}
}
}
return 0;
}
int main()
{
n=read(); h=read();
memset(head,-1,sizeof(head));
for(int i=0;i<=n;++i)
{
add(n+1,i,0); //这里的超级原点是n+1
}
for(int i=1;i<=h;++i)
{
edge1[i].b=read();
edge1[i].e=read();
edge1[i].t=read();
add(edge1[i].e,edge1[i].b-1,-edge1[i].t); //建边方式
}
for(int i=1;i<=n;++i)
{
add(i,i-1,0);
add(i-1,i,1);
}
spfa();
write(-dis[0]); //输入的时候是负边权,输出要取反;
return 0;
}边栏推荐
- Kingdee International: Lost in half a year and last year, how does the business model of frantically burning money continue
- 推出 Space On-Premises (本地部署版) Beta 版!
- [数据集][VOC]男女数据集voc格式6188张
- typescript ‘props‘ is declared but its value is never read 解决办法
- optional
- postgres 多个变量填充字符串,字串格式化
- npm does not recognize the "npm" item as the name of a cmdlet, function, script file, or runnable program.Please check the spelling of the name, and if the path is included, make sure the path is corr
- 【npm install 报错问题合集】- npm ERR! code ENOTEMPTY npm ERR! syscall rmdir
- CAT1 4G+Ethernet development board Tencent cloud mobile phone WeChat applet display temperature and delivery control
- Node installation and environment configuration
猜你喜欢
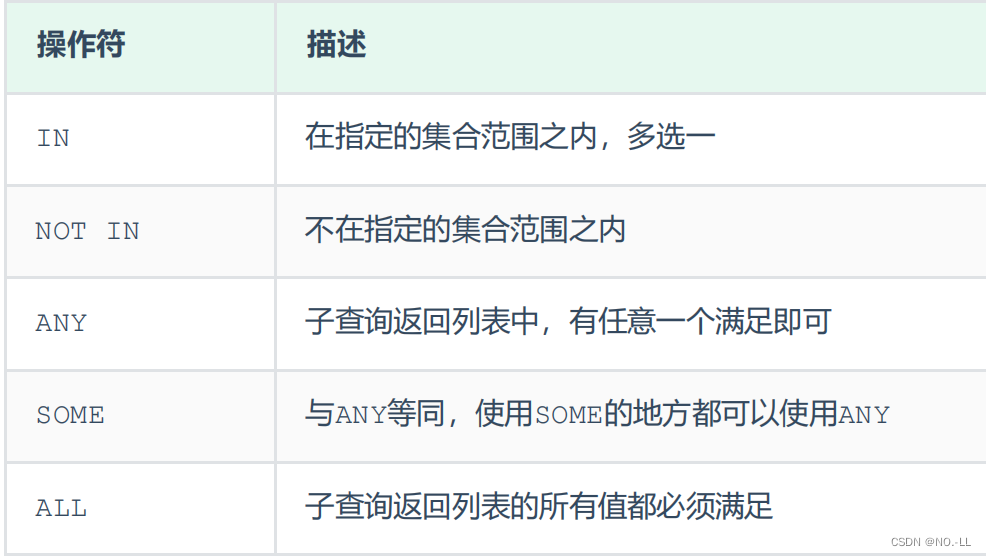
MySQL - 多表查询与案例详解

8/1 思维+扩展欧几里得+树上dp

Analysis of the source code of the JS UI framework of Hongmeng system
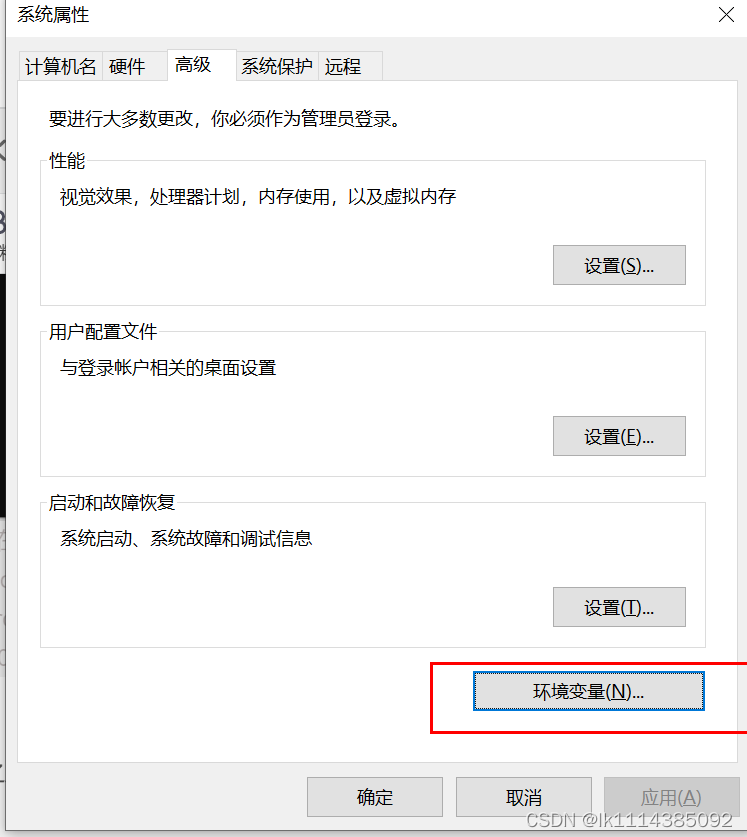
Node installation and environment variable configuration
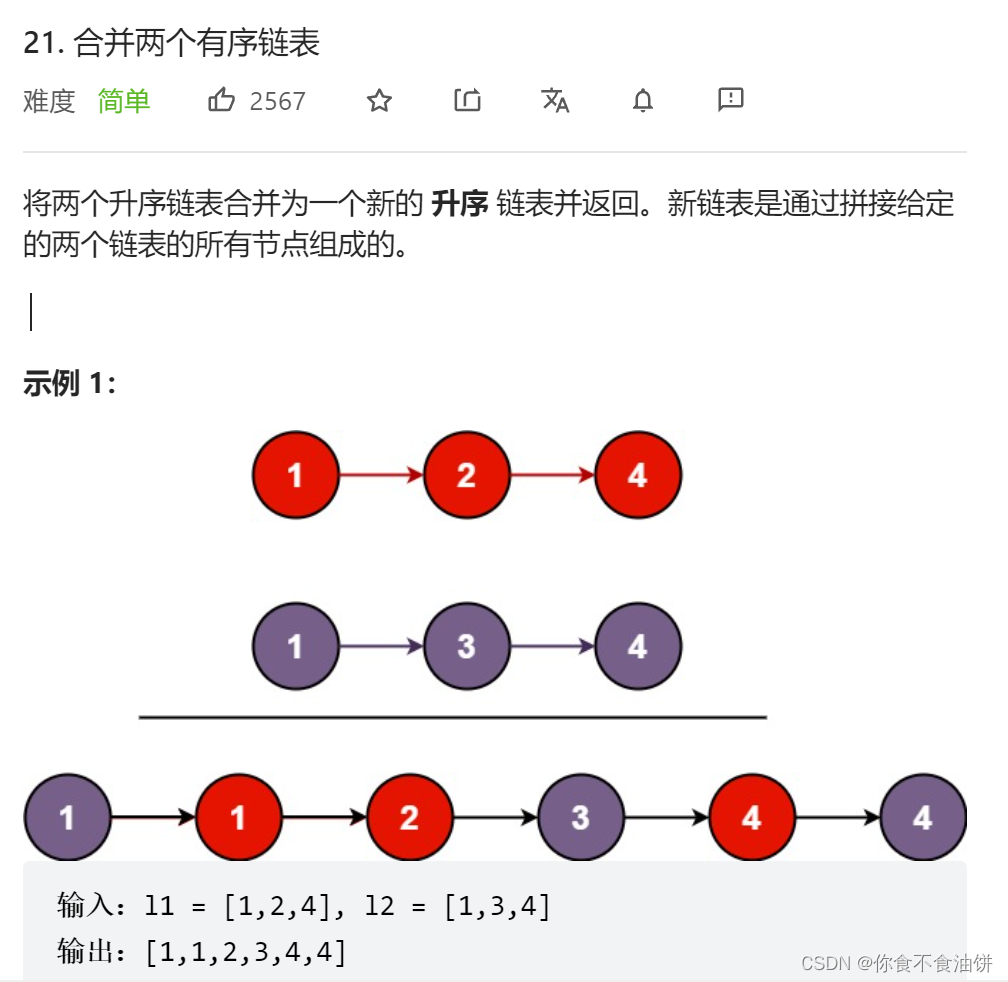
leetcode solves the linked list merge problem in one step
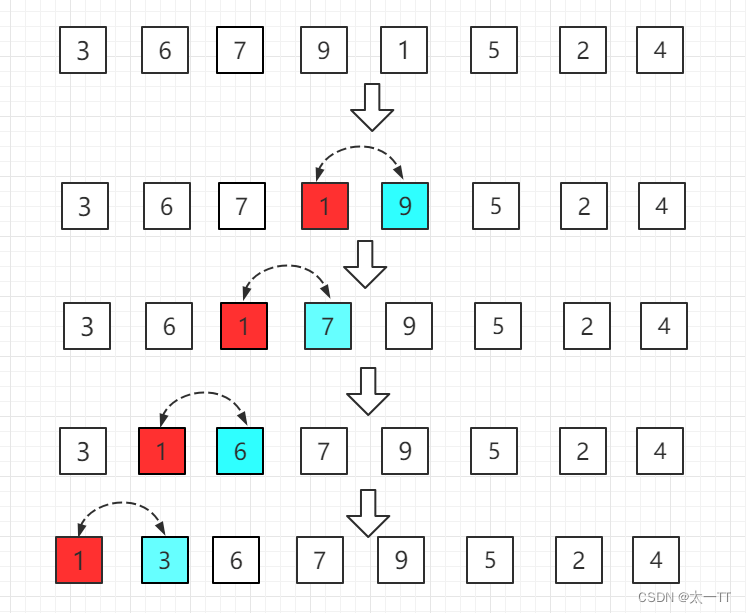
【21天学习挑战赛】顺序查找

推出 Space On-Premises (本地部署版) Beta 版!
Tips for programmers to write PPT

BGP+MPLS Comprehensive Experiment

MySQL高级语句(一)
随机推荐
Kingdee International: Lost in half a year and last year, how does the business model of frantically burning money continue
MarkDown Formula Instruction Manual
MySQL Advanced SQL Statements
MySQL classic 50 practice questions and the most detailed analysis of the whole network
MySQL高级语句(一)
有人开源全凭“为爱发电”,有人却用开源“搞到了钱”
Analysis of port 9848 error at startup of Nacos client (non-version upgrade problem)
CAT1 4G+以太网开发板腾讯云手机微信小程序显示温度和下发控制
MySQL高级-MVCC(超详细整理)
Toolbox App 1.25 New Features at a Glance | Version Update
NPM 安装指定版本包的方法及版本号查看
Dataset:机器学习中常用数据集下载链接集合之详细攻略
MySQL database video tutorial from beginner to proficient
Nacos installation configuration and single-machine deployment tutorial
科技赋能拉萨之“肺”,华为助力拉鲁湿地智慧管理守护绿水青山
How does abaqus quickly import the assembly of other cae files?
HCIP 第一天
Launch Space on-premises deployment (local) Beta!
Tips for programmers to write PPT
Not annotated parameter overrides @NonNullApi parameter