当前位置:网站首页>(7/29)基础板子最小生成树prim+kruskal
(7/29)基础板子最小生成树prim+kruskal
2022-07-30 21:05:00 【咸蛋_dd】
1.prim算法求最小生成树
给定一个 nn 个点 mm 条边的无向图,图中可能存在重边和自环,边权可能为负数。
求最小生成树的树边权重之和,如果最小生成树不存在则输出
impossible。给定一张边带权的无向图 G=(V,E)G=(V,E),其中 VV 表示图中点的集合,EE 表示图中边的集合,n=|V|n=|V|,m=|E|m=|E|。
由 VV 中的全部 nn 个顶点和 EE 中 n−1n−1 条边构成的无向连通子图被称为 GG 的一棵生成树,其中边的权值之和最小的生成树被称为无向图 GG 的最小生成树。
输入格式
第一行包含两个整数 nn 和 mm。
接下来 mm 行,每行包含三个整数 u,v,wu,v,w,表示点 uu 和点 vv 之间存在一条权值为 ww 的边。
输出格式
共一行,若存在最小生成树,则输出一个整数,表示最小生成树的树边权重之和,如果最小生成树不存在则输出
impossible。数据范围
1≤n≤5001≤n≤500,
1≤m≤1051≤m≤105,
图中涉及边的边权的绝对值均不超过 1000010000。输入样例:
4 5 1 2 1 1 3 2 1 4 3 2 3 2 3 4 4输出样例:
6#include <bits/stdc++.h>
using namespace std;
const int N=100010;
int res=0;
int mp[510][510];
bool st[510];
int dis[510];
int n,m;
const int inf=0x3f3f3f3f;
int prim()
{
for(int i=0;i<n;i++)
{
int t=-1;
for(int j=1;j<=n;j++)
{
if(st[j]==0&&(t==-1||dis[j]<dis[t]))
t=j;
}
if(i&&dis[t]==inf) return inf;
st[t]=true;
if(i&&dis[t]!=inf)
res+=dis[t];
for(int j=1;j<=n;j++)
{
if(dis[j]>mp[t][j])
dis[j]=mp[t][j];
}
}
return res;
}
int main()
{
int a,b,c;
scanf("%d %d",&n,&m);
memset(dis,inf,sizeof(dis));
memset(mp,inf,sizeof(mp));
while(m--)
{
scanf("%d %d %d",&a,&b,&c);
mp[a][b]=mp[b][a]=min(mp[a][b],c);
}
int t=prim();
if(t==inf)
printf("impossible\n");
else
printf("%d\n",t);
return 0;
}2.kruskal算法
给定一个 nn 个点 mm 条边的无向图,图中可能存在重边和自环,边权可能为负数。
求最小生成树的树边权重之和,如果最小生成树不存在则输出
impossible。给定一张边带权的无向图 G=(V,E)G=(V,E),其中 VV 表示图中点的集合,EE 表示图中边的集合,n=|V|n=|V|,m=|E|m=|E|。
由 VV 中的全部 nn 个顶点和 EE 中 n−1n−1 条边构成的无向连通子图被称为 GG 的一棵生成树,其中边的权值之和最小的生成树被称为无向图 GG 的最小生成树。
输入格式
第一行包含两个整数 nn 和 mm。
接下来 mm 行,每行包含三个整数 u,v,wu,v,w,表示点 uu 和点 vv 之间存在一条权值为 ww 的边。
输出格式
共一行,若存在最小生成树,则输出一个整数,表示最小生成树的树边权重之和,如果最小生成树不存在则输出
impossible。数据范围
1≤n≤1051≤n≤105,
1≤m≤2∗1051≤m≤2∗105,
图中涉及边的边权的绝对值均不超过 10001000。输入样例:
4 5 1 2 1 1 3 2 1 4 3 2 3 2 3 4 4输出样例:
6基本思路:先将所有边权按权重大小排序(用结构体存储),然后枚举每条边,利用并查集,如果两点不在一个连通块内,就将这条边加入集合,并且将两点放到同一个连通块内,
#include <bits/stdc++.h>
using namespace std;
const int N=200010;
int p[N];
struct node
{
int st,ed,w;
}a[N];
int Find(int x)
{
if(p[x]!=x)
p[x]=Find(p[x]);
return p[x];
}
bool cmp(struct node x,struct node y)
{
return x.w<y.w;
}
int main()
{
int t,x,y,i,j,n,m;
scanf("%d %d",&n,&m);
for(i=1;i<=n;i++)
{
p[i]=i;
}
for(i=1;i<=m;i++)
{
scanf("%d %d %d",&a[i].st,&a[i].ed,&a[i].w);
}
sort(a+1,a+1+m,cmp);
int cnt=0;
int ans=0;
for(i=1;i<=m;i++)
{
int x=Find(a[i].st);
int y=Find(a[i].ed);
if(x!=y)
{
p[x]=y;
cnt++;
ans+=a[i].w;
}
}
if(cnt<n-1)
printf("impossible\n");
else
printf("%d",ans);
return 0;
}
边栏推荐
猜你喜欢
Image Restoration by Estimating Frequency Distribution of Local Patches

MySQL 视图(详解)
![[Deep Learning] Understanding of Domain Adaptation in Transfer Learning and Introduction of 3 Techniques](/img/51/b351385c1f0f4e0a545e54c8ae7491.png)
[Deep Learning] Understanding of Domain Adaptation in Transfer Learning and Introduction of 3 Techniques

数字货币期货现货交易技巧,把握关键进场的买入点!(纯干货)

MySQL的on duplicate key update 的使用

IDEA2018.3.5取消双击Shift快捷键

flyway的快速入门教程
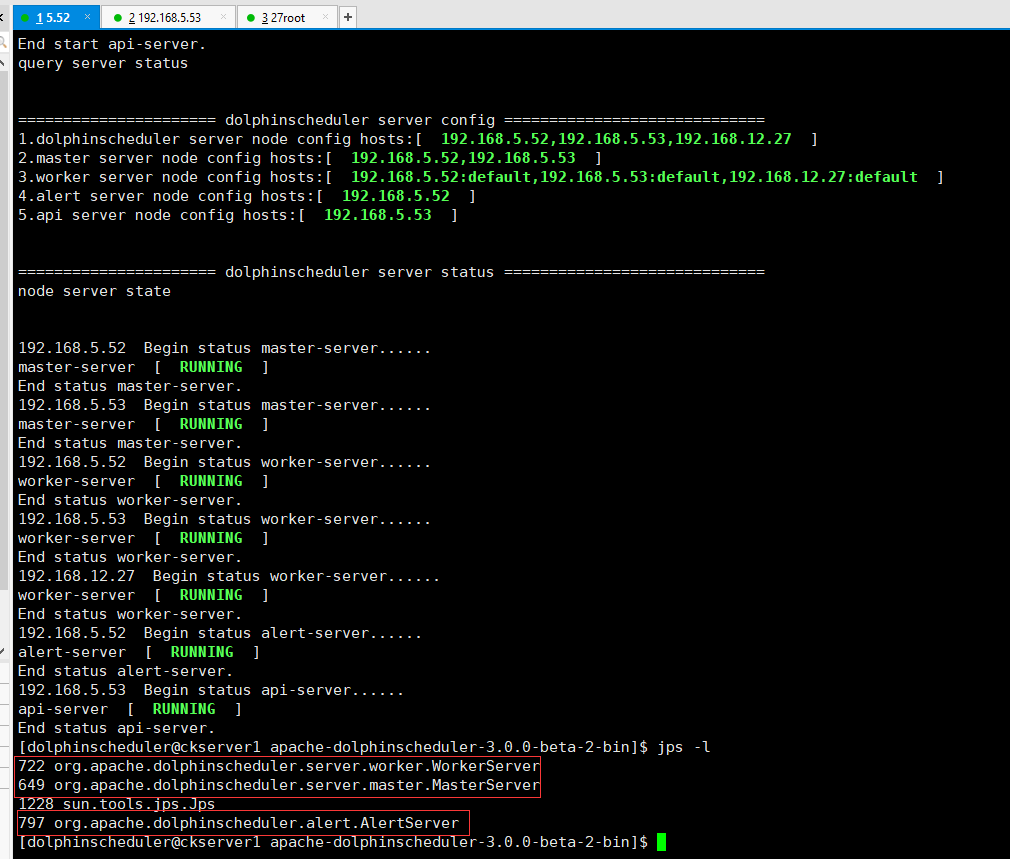
Apache DolphinScheduler新一代分布式工作流任务调度平台实战-上

化二次型为标准型
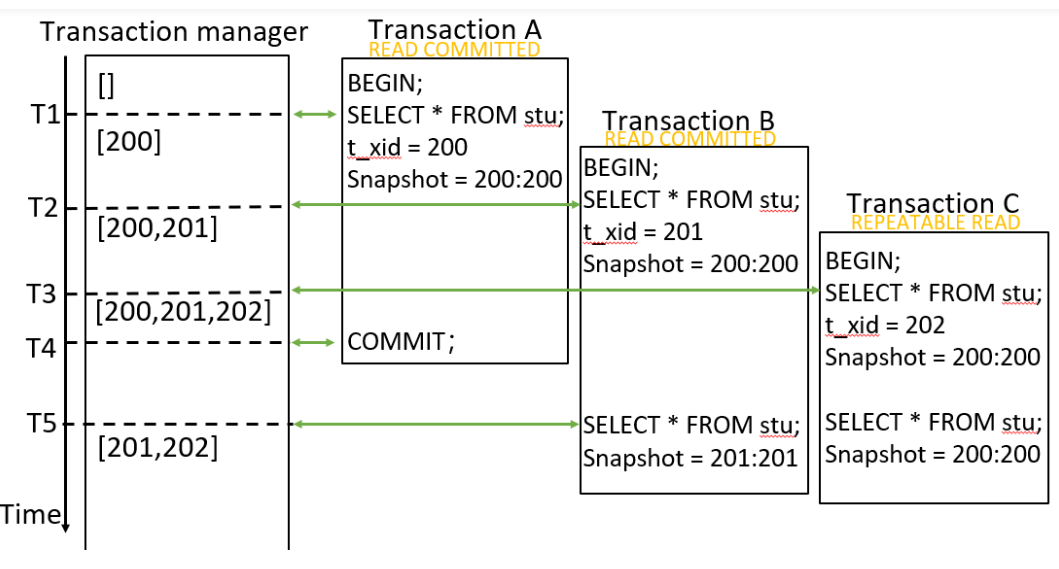
KingbaseESV8R6 snapshot too old的配置和测试
随机推荐
Deep Non-Local Kalman Network for VideoCompression Artifact Reduction
弹性盒子模型
Deep Kalman Filter Network for Video Compression Artifact Removal
KEIL problem: [keil Error: failed to execute 'C:\Keil\ARM\ARMCC']
bebel系列- 插件开发
GPGGA NTRIP RTCM Notes
DPW-SDNet: Dual Pixel-Wavelet Domain Deep CNNs for Soft Decoding of JPEG-Compressed Images
多线程获取官方汇率
tcp协议传输中的粘包问题
Why do so many people who teach themselves software testing give up later...
mysql8安装步骤教程
Generate OOM records in a production environment. Conclusion: Don't be lazy to query useless fields unless you are completely sure.
IDEA2018.3.5取消双击Shift快捷键
如何制作deb包
flyway的快速入门教程
MySQL的Replace用法详解
关于SFML Rect.inl文件报错的问题
MySQL Workbench 安装及使用
6.3有定型性 第七章
《快速掌握QML》第六章 动画