当前位置:网站首页>LeetCode 0150. 逆波兰表达式求值
LeetCode 0150. 逆波兰表达式求值
2022-08-01 05:23:00 【Tisfy】
【LetMeFly】150.逆波兰表达式求值
力扣题目链接:https://leetcode.cn/problems/evaluate-reverse-polish-notation/
根据 逆波兰表示法,求表达式的值。
有效的算符包括 +、-、*、/ 。每个运算对象可以是整数,也可以是另一个逆波兰表达式。
注意 两个整数之间的除法只保留整数部分。
可以保证给定的逆波兰表达式总是有效的。换句话说,表达式总会得出有效数值且不存在除数为 0 的情况。
示例 1:
输入:tokens = ["2","1","+","3","*"] 输出:9 解释:该算式转化为常见的中缀算术表达式为:((2 + 1) * 3) = 9
示例 2:
输入:tokens = ["4","13","5","/","+"] 输出:6 解释:该算式转化为常见的中缀算术表达式为:(4 + (13 / 5)) = 6
示例 3:
输入:tokens = ["10","6","9","3","+","-11","*","/","*","17","+","5","+"] 输出:22 解释:该算式转化为常见的中缀算术表达式为: ((10 * (6 / ((9 + 3) * -11))) + 17) + 5 = ((10 * (6 / (12 * -11))) + 17) + 5 = ((10 * (6 / -132)) + 17) + 5 = ((10 * 0) + 17) + 5 = (0 + 17) + 5 = 17 + 5 = 22
提示:
1 <= tokens.length <= 104tokens[i]是一个算符("+"、"-"、"*"或"/"),或是在范围[-200, 200]内的一个整数
逆波兰表达式:
逆波兰表达式是一种后缀表达式,所谓后缀就是指算符写在后面。
- 平常使用的算式则是一种中缀表达式,如
( 1 + 2 ) * ( 3 + 4 )。 - 该算式的逆波兰表达式写法为
( ( 1 2 + ) ( 3 4 + ) * )。
逆波兰表达式主要有以下两个优点:
- 去掉括号后表达式无歧义,上式即便写成
1 2 + 3 4 + *也可以依据次序计算出正确结果。 - 适合用栈操作运算:遇到数字则入栈;遇到算符则取出栈顶两个数字进行计算,并将结果压入栈中
方法一:栈模拟
如果懂了什么是逆波兰表达式,那么这道题将会非常简单。
逆波兰表达式的计算要比求表达式的逆波兰容易得多。
使用一个栈,
遍历逆波兰表达式,如果遇到运算符,就从栈中取出对应个数的元素,并进行运算,再把结果入栈。
例如,如果遇到了
+,就从栈中取出两个元素(因为加号是双目运算符),求和并将结果入栈。
注意,栈中的顺序与原顺序是反着的,先出栈的是位置较后的元素。
如果遇到数字,就之间入栈。
- 时间复杂度 O ( n ) O(n) O(n),其中 n n n是逆波兰表达式中的元素/运算符个数
- 空间复杂度 O ( n ) O(n) O(n)
AC代码
C++
class Solution {
public:
int evalRPN(vector<string>& tokens) {
stack<int> st;
for (string& s : tokens) {
if (s == "+" || s == "-" || s == "*" || s == "/") {
int second = st.top();
st.pop();
int first = st.top();
st.pop();
if (s == "+")
st.push(first + second);
else if (s == "-")
st.push(first - second);
else if (s == "*")
st.push(first * second);
else if (s == "/")
st.push(first / second);
}
else {
st.push(atoi(s.c_str()));
}
}
return st.top();
}
};
同步发文于CSDN,原创不易,转载请附上原文链接哦~
Tisfy:https://letmefly.blog.csdn.net/article/details/126084278
边栏推荐
猜你喜欢

(2022牛客多校四)A-Task Computing (排序+动态规划)

pytorch、tensorflow对比学习—功能组件(优化器、评估指标、Module管理)
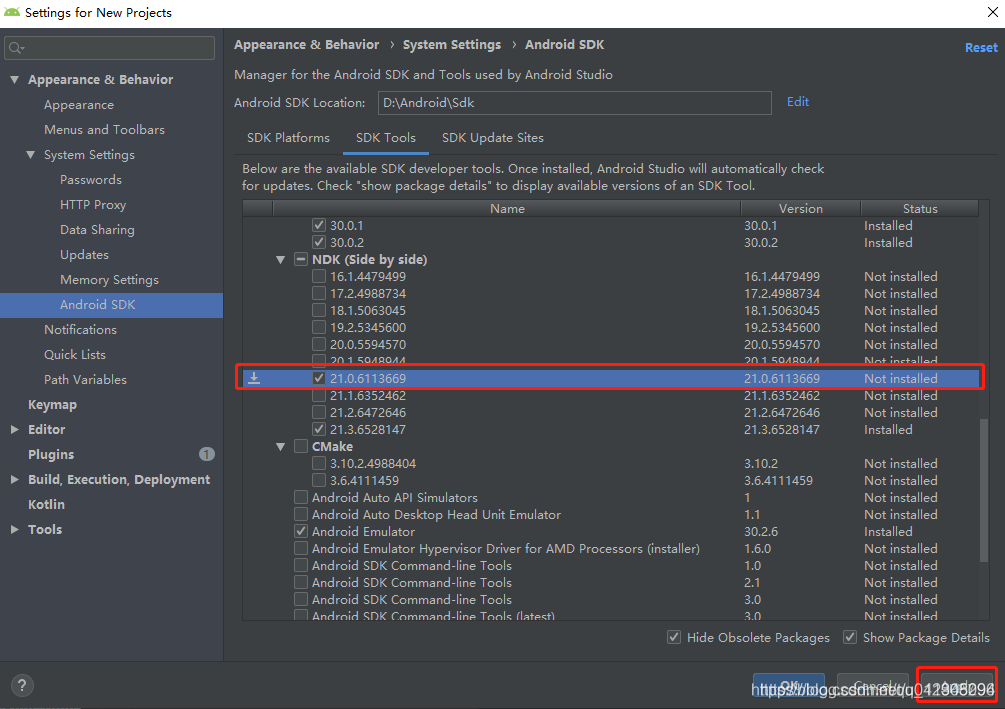
NDK does not contain any platforms problem solving

可视化全链路日志追踪
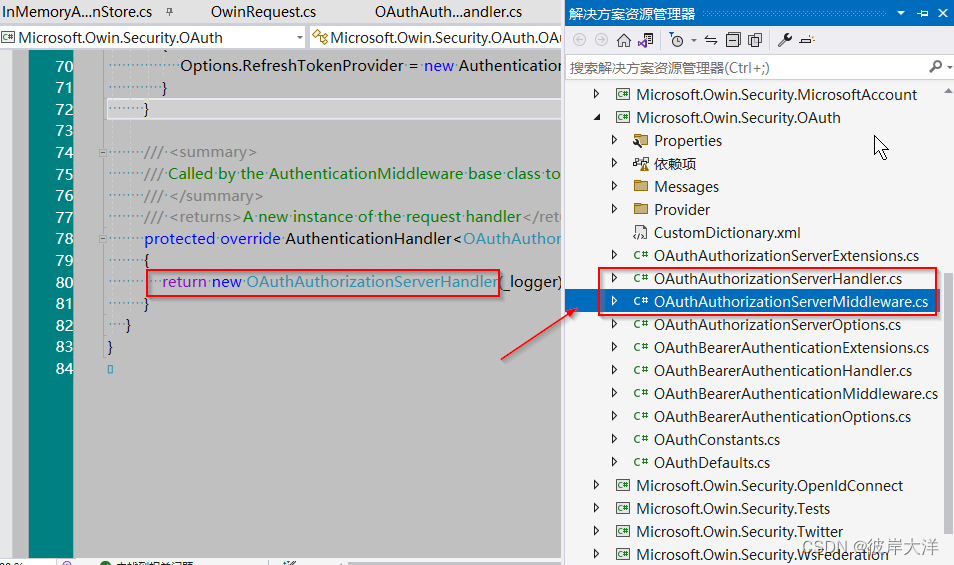
AspNet.WebApi.Owin 自定义Token请求参数

AspNet.WebApi.Owin custom Token request parameters
2022.7.26 Mock Competition
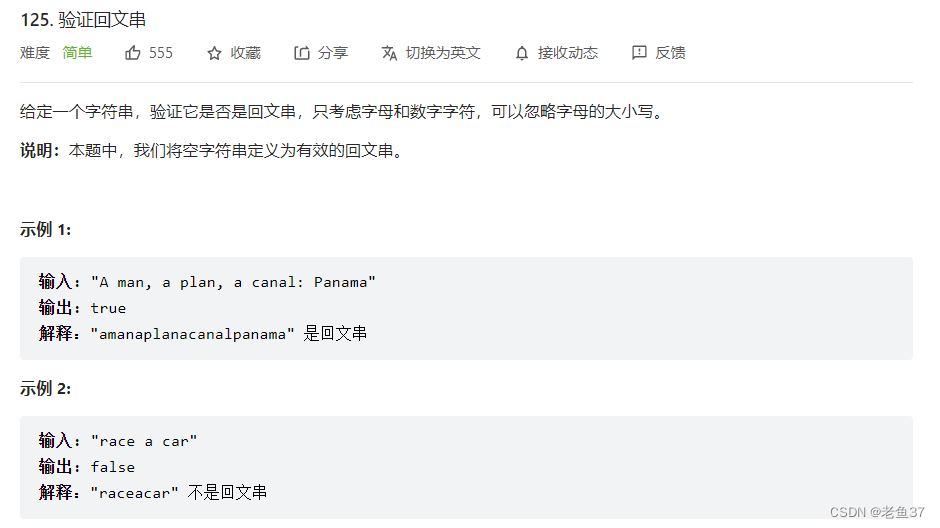
leetcode125 Verify palindrome string
leetcode43 字符串相乘

状态压缩dp
随机推荐
零序电流继电器器JL-8C-12-2-2
Asynchronous reading and writing of files
Selenium:浏览器操作
leetcode125 验证回文串
USB3.0:VL817Q7-C0的LAYOUT指南(二)
【MySQL必知必会】 表的优化 | 充分利用系统资源
vim configuration + ctag is as easy to read code as source insight
冲刺金九银十,Android开发面试(内含面试资料|面试题|源码)
LeetCode 231. 2 的幂
pytorch、tensorflow对比学习—张量
MySQL Practice Summary -
WPF项目-按着键盘方向键,移动格子盒子效果
使用string 容器翻转 字母
LeetCode 1189. “气球” 的最大数量
uva12326
[target detection] YOLOv7 theoretical introduction + practical test
中国的机器人增长
对话MySQL之父:一个优秀程序员可抵5个普通程序员
Jupyter shortcuts
Robot_Framework: Assertion