2022.7.26 Mock Competition

T1 tree

  Stupid during the exam,Run straight to both sides $dfs$ Number connected blocks,Then output a small number.It's actually easy to get caught $hack$ 掉,For example, if you dye a connected block, you can dye multiple blocks of the original image at the same time,Just like this picture：

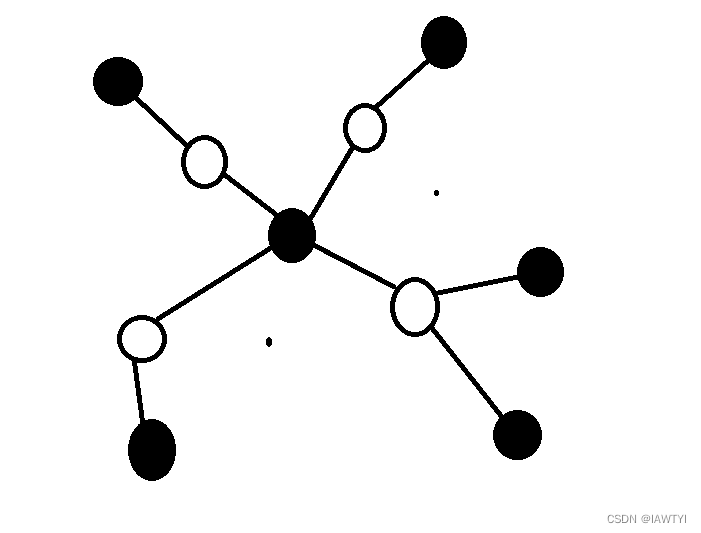
  In this picture, first change the point in the middle and then change the circle in the middle,Only changed twice.But the answer to the connected block is just that $4$.So we can't count directly.

  受这个 $hack$ 的启发,We can consider picking a point as the root,Then each time the connected block where the root node is located is changed to expand downwards.But this should still not be optimal,Because if it is extended to a certain layer, there is only one point：

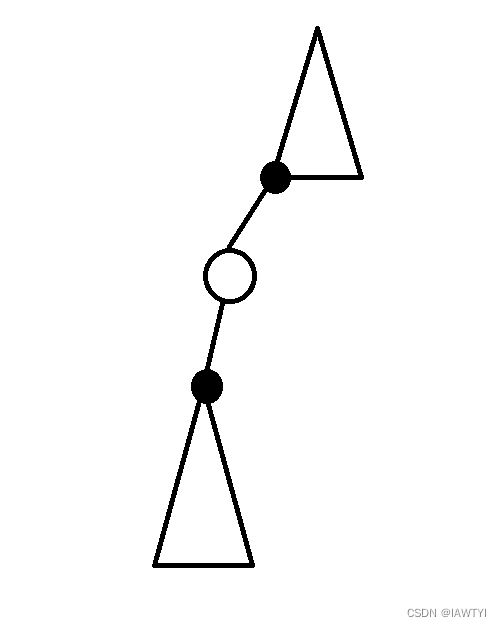
  We can take one step to dye this white into black first,This directly merges the upper and lower layers together（When it is expanded, it can be regarded as a layer and directly changed in one step）,It took one step to do what we just did in two steps.So we want to make what we just did the best,There are requirements for the root we choose.

  We can find out by drawing some pictures by ourselves,As long as the point we pick is the center point of the tree's diameter（The path length is odd）There will definitely not be such a situation where there is only one layer,Because we split the diameter in half,The diameter of the left and right parts must be symmetrical（The previous connected block has been shrunk to a point）,So that doesn't happen.So we directly output the general length of the path（向下取整）就好了（也就是层数）.

  对于偶数的情况,We will find that the answer is also half the length of the diameter,所以可以统一处理.

#include<bits/stdc++.h>
using namespace std;
#define in read()
#define MAXN 200200
#define MAXM MAXN << 2

inline int read(){
    
	int x = 0; char c = getchar();
	while(c < '0' or c > '9') c = getchar();
	while('0' <= c and c <= '9'){
    
		x = x * 10 + c - '0'; c = getchar();
	}
	return x;
}

int n = 0, cnt = 0;
int f[MAXN] = {
     0 };
int b[MAXN] = {
     0 };
int fa[MAXN] = {
     0 };
struct Tree{
    
	int tot;
	int first[MAXN];
	int   nxt[MAXM];
	int    to[MAXM];
	int color[MAXN];
	inline void add(int x, int y){
    
		nxt[++tot] = first[x];
		first[x] = tot; to[tot] = y;
	}
}T1, T2;

int find(int x){
    
	if(x == fa[x]) return x;
	return fa[x] = find(fa[x]);
}

void merge(int x, int y){
    
	int fax = find(x), fay = find(y);
	fa[fax] = fay; 
}

int ans = 0, p = 1;
int dep[MAXN] = {
     0 };
void dfs(int x, int fa){
    
	dep[x] = dep[fa] + 1;
	if(dep[x] > ans) ans = dep[x], p = x;
	for(int e = T2.first[x]; e; e = T2.nxt[e]){
    
		int y = T2.to[e];
		if(y == fa) continue;
		dfs(y, x);
	}
} 

int main(){
    
	n = in; T1.tot = 1;
	for(int i = 1; i <= n; i++) T1.color[i] = in, fa[i] = i;
	for(int i = 1; i < n; i++){
    
		int x = in, y = in;
		if(T1.color[x] == T1.color[y]) merge(x, y);
		T1.add(x, y), T1.add(y, x);
	}
	for(int i = 1; i <= n; i++){
    
		int x = find(i);
		if(!f[x]) b[x] = ++cnt, b[i] = cnt, f[x] = 1;
		else b[i] = b[x];
	}
	for(int i = 1; i <= T1.tot; i++){
    
		int x = T1.to[i], y = T1.to[i ^ 1];
		if(b[x] != b[y]) T2.add(b[x], b[y]);
	}
	dfs(1, 0);
	memset(dep, 0, sizeof dep), ans = 0;
	dfs(p, 0);
 	cout << (ans >> 1) << '\n';
	return 0;
} 

T2 multisets

  $wss$ Big guy's approach $TJ$ The time complexity is still low Orz orz orz orz.

  We consider enumerating the range from small to large,Then enumerate how many this number is from largest to smallest.In this way, the sets that we enumerate to satisfy this condition are obviously increasing sequentially.So we calculate to consider inclusion $k$ 个 $x$ How many sets are there in total,It is calculated as the contribution of this set to the ranking.

  我们假设一共有 $m$ 个 $x$,and their subscripts are $id{x}_1,id{x}_2,\cdots ,id{x}_m$,那么贡献就是：

$$\sum _{i=0}^{m-k+1}(id{x}_{i+1}-id{x}_i)(id{x}_{i+k}-id{x}_{i+k-1})$$

  But the subscript used here will obviously exceed $m$,所以如果 $id{x}_i-id{x}_{i-1}<0$,Let's make it equal $1$ 就好了.

#include<bits/stdc++.h>
using namespace std;
#define in read()
#define MAXN 100100

inline int read(){
    
	int x = 0; char c = getchar();
	while(c < '0' or c > '9') c = getchar();
	while('0' <= c and c <= '9'){
    
		x = x * 10 + c - '0'; c = getchar();
	} 
	return x;
}

int s[MAXN] = {
     0 };
int n = 0; int k = 0;
vector<int> pos[MAXN];                                                                        // pos[s[i]] : 为 s[i] set of subscripts
int have[MAXN] = {
     0 };                                                                       // have[s[i]] : s[i] 
int ans[MAXN] = {
     0 };                                                                        // ans[i] : i number in the answer
struct Tnode{
    
	int ll, lr;
	int rl, rr;
	Tnode() {
    }
	Tnode(int a, int b, int c, int d) {
     ll = a, lr = b, rl = c, rr = d; }
	bool operator < (const Tnode &rhs) const {
     return ll < rhs.ll; }
}; set<Tnode> st, temp;                                                                       // 答案集合

int query(int p, int num){
                                                                        // 询问 st How many sets are there to satisfy there num 个 p
	int l = 1, r = l + num - 1;
	int ll = 0, lr = 0, rl = 0, rr = 0;
	int ans = 0;
	set<Tnode>::iterator z;
	while(r + 1 < pos[p].size()){
    
		ll = pos[p][l - 1] + 1, lr = pos[p][l];
		rl = pos[p][r], rr = pos[p][r + 1] - 1;
		z = st.upper_bound(Tnode(lr, 0, 0, 0));
		while(z != st.begin()){
    
			z--;
			if((*z).lr < ll) break;
			int LL = max((*z).ll, ll), LR = min((*z).lr, lr);
			int RL = max((*z).rl, rl), RR = min((*z).rr, rr);
			if(LL <= LR and RL <= RR) ans += (LR - LL + 1) * (RR - RL + 1);
		}
		l++, r++;
	}
	return ans;
}

void getnum(int p){
                                                                               // Determine the answer set p 有多少个
	ans[p] = have[p];
	while(ans[p]){
    
		int temp = query(p, ans[p]);
		if(temp >= k) return;
		ans[p]--, k -= temp;
	}
}

void merge(int p, int num){
                                                                       // Select contains from the initial set of answers num 个 p 的集合
	int l = 1, r = l + num - 1;
	int ll = 0, lr = 0, rl = 0, rr = 0;
	set<Tnode>::iterator z;
	while(r + 1 < pos[p].size()){
    
		ll = pos[p][l - 1] + 1, lr = pos[p][l];
		rl = pos[p][r], rr = pos[p][r + 1] - 1;
		z = st.upper_bound(Tnode(lr, 0, 0, 0));
		while(z != st.begin()){
    
			z--;
			if((*z).lr < ll) break;
			int LL = max((*z).ll, ll), LR = min((*z).lr, lr);                                 // 取交集
			int RL = max((*z).rl, rl), RR = min((*z).rr, rr);
			if(LL <= LR and RL <= RR) temp.insert(Tnode(LL, LR, RL, RR));
		}
		l++, r++;
	}
	st.clear(), z = temp.begin();
	while(z != temp.end()) st.insert(*z), z++;
	temp.clear();
}

int main(){
    
	n = in; k = in;
	for(int i = 1; i <= n; i++) pos[i].push_back(0);                                          // It will be convenient to check the predecessor and successor later
	for(int i = 1; i <= n; i++) s[i] = in, have[s[i]]++, pos[s[i]].push_back(i);
	st.insert(Tnode(1, n, 1, n));
	for(int i = 1; i <= n; i++) pos[i].push_back(n + 1);
	for(int i = 1; i <= n; i++)
		if(have[i]){
    
			getnum(i);
			merge(i, ans[i]);
		}
	for(int i = 1; i <= n; i++)
		for(int j = 1; j <= ans[i]; j++) cout << i << ' ';
	return 0;
} 

  This approach looks very violent but is actually very efficient,Let's analyze the complexity.我们发现,调用 $getnum()$ The number of times this function is $s$ The number of species in the number,而在每次 $getnum()$ 时调用的 $query()$ The number of times is the number of such numbers,So a total of calls $query()$ The number of times that is $O(n)$ 的.

  在一次 $query()$ 种,There will be one for every collection $O(\log n)$ 的查询,所以 $query()$ 的复杂度就是 $O(st.size()\times \log n)$.And because the description of this topic guarantees that the data is randomly generated （Although the title description says that this is useless for solving the problem, it is still used here qwq),所以我们可以知道在 $s$ 中,一个数 $s_i$ The expected number of occurrences is $1$.And every time we increase the number of sets, there is only a certain number $s$ 分成若干部分,所以 $st.size()$ will always remain within the constant range,所以 $query()$ The complexity can be seen as $O(\log n)$ 的.所以总的复杂度就是 $O(n\log n)$ 的了 比 TJ 的 O(nlog^2 n) 还要优秀.

T3 maximize

  我们考虑 $a_i$ Condition for longevity contribution to answer,We can find that every deletion of a number,It is equivalent to moving all the numbers to the right of the number one space forward.Obviously if the deleted array is satisfied $a_i=i$ 那么就说明 $a_i$ will contribute to the answer,But this may be the result of moving to the left,所以要满足 $a_i\ge i$ to be able to contribute to the answer.

  and if you want to contribute,We are ahead $i$ deleted from the number $i-a_i$ number to allow $a_i$ Finally fell to the subscript as $a_i$ 的地方.The title also asks to delete at most $k$ 个数,So be satisfied $i-a_i\le k$.

  同理,如果 $a_i>n-k$ Then its value is no longer a deletion $k$ after $[1,n-k]$ subscript this range,So no contribution can be made,所以要满足 $a_i\le n-k$.

  So now we get three conditions：

$$\begin{array}{rl}{a}_i\ge & i\\ a_i\ge & i-k\\ a_i\le & n-k\end{array}$$

  我们考虑一个 $j>i$ 并且 $j$ Can also make contributions to what conditions we need to set.The two of them need to be deleted respectively to return to their positions $a_i-i$ 个数和 $a_j-j$ 个数.又因为 $j>i$,所以$j$ The number previously deleted is greater than or equal to $i$ 的.就是说：

$$a_i-i\le a_j-j$$

  于是：

$$\begin{array}{rl}i<& j\\ a_i<& a_j\\ a_i-i\le & a_j-j\end{array}$$

  We found that these three conditions can be inferred from each other（Know two push one）,So we pick two：

$$\begin{array}{rl}{a}_i<& a_j\\ a_i-i\le & a_j-j\end{array}$$

  This is obviously a two-dimensional partial order（It is equivalent to the longest ascending subsequence）.

  Now let's address the question of the correctness of this approach,对于 $i<j$ 显然满足：

$$(a_j-j)-(a_i-i)\le j-i$$

  We also have to satisfy the deletion $j$ The number of later deletions is greater than $k$：

$$(a_i-j)-(n-j)\ge k$$

  This obviously holds,So there is no problem with the sequence constructed in this way.

#include<bits/stdc++.h>
using namespace std;
#define in read()
#define MAXN 500500

inline int read(){
    
	int x = 0; char c = getchar();
	while(c < '0' or c > '9') c = getchar();
	while('0' <= c and c <= '9'){
    
		x = x * 10 + c - '0'; c = getchar();
	}
	return x;
}

int n = 0; int k = 0;
int mx = 0; int cnt = 0;
int c[MAXN << 2] = {
     0 };
struct Tnode{
    
	int idx, val;
	bool operator < (const Tnode &rhs) const {
    
		if(idx - val == rhs.idx - rhs.val)
			return val < rhs.val;
		return idx - val < rhs.idx - rhs.val;
	}
}a[MAXN];

inline int lowbit(int x) {
     return x & -x; }
void add(int x, int y) {
     for(; x <= mx; x += lowbit(x)) c[x] = max(c[x], y); }
int query(int x){
    
	int ans = 0;
	for(; x; x -= lowbit(x)) ans = max(ans, c[x]);
	return ans;
}

int main(){
    
	n = in; k = in;
	for(int i = 1; i <= n; i++){
    
		int w = in;
		if(w >= i - k and w <= n - k and w <= i)
			a[++cnt] = (Tnode){
     i, w }, mx = max(mx, w);
	} sort(a + 1, a + cnt + 1);
	int ans = 0;
	for(int i = 1; i <= cnt; i++){
    
		int temp = query(a[i].val - 1) + 1;
		if(n - a[i].val >= k) ans = max(ans, temp);
		add(a[i].val, temp);
	}
	cout << ans << '\n';
	return 0;
} 

T4 journey

  $20pts$ 很简答,就是枚举 $x,y$,Note that contributions are only possible in $lca$ 处,So it can be calculated directly,时间复杂度：$O(n^2\log n)$.

#include<bits/stdc++.h>
using namespace std;
#define in read()
#define MAXN 100100
#define MAXM MAXN << 2

inline int read(){
    
	int x = 0; char c = getchar();
	while(c < '0' or c > '9') c = getchar();
	while('0' <= c and c <= '9'){
    
		x = x * 10 + c - '0'; c = getchar();
	}
	return x;
}

int n = 0;
int tot = 0;
int first[MAXN] = {
     0 };
int   nxt[MAXM] = {
     0 };
int    to[MAXM] = {
     0 };
int   ans[MAXN] = {
     0 };
int   can[MAXN] = {
     0 };
inline void add(int x, int y){
    
	nxt[++tot] = first[x];
	first[x] = tot; to[tot] = y;
}

int dep[MAXN] = {
     0 };
int val[MAXN] = {
     0 };
int f[MAXN][50] = {
     0 };
void prework(int x, int fa){
    
	dep[x] = dep[fa] + 1, val[x] += val[fa];
	for(int i = 0; i <= 30; i++) f[x][i + 1] = f[f[x][i]][i];
	for(int e = first[x]; e; e = nxt[e]){
    
		int y = to[e];
		if(y == fa) continue;
		f[y][0] = x; prework(y, x);
	}
}

int Lca(int x, int y){
    
	if(dep[x] < dep[y]) swap(x, y);
	for(int i = 30; i >= 0; i--){
    
		if(dep[f[x][i]] >= dep[y]) x = f[x][i];
		if(x == y) return x;
	}
	for(int i = 30; i >= 0; i--)
		if(f[x][i] != f[y][i])
			x = f[x][i], y = f[y][i];
	return f[x][0]; 
}

int main(){
    
// freopen("a.in", "r", stdin); 
	n = in;
	for(int i = 1; i < n; i++){
    
		int y = in; add(i + 1, y), add(y, i + 1); }
	for(int i = 1; i <= n; i++) val[i] = in;
	prework(1, 0);
	for(int x = 1; x <= n; x++)
		for(int y = 1; y <= n; y++){
    
			if(x == y) continue;
			int lca = Lca(x, y);
			if(x == lca or y == lca) continue;
			int p = val[x] - val[f[lca][0]];
			int q = val[y] - val[f[lca][0]];
			ans[lca] = max(ans[lca], p ^ q), can[lca] = 1;
		}
	for(int i = 1; i <= n; i++)
		if(can[i]) cout << ans[i] << ' ';
		else cout << -1 << ' ';
	puts("");
	return 0;
}

  The third point is a chrysanthemum diagram,It is easy to find that only the root node has the answer,So the problem becomes $n-1$ Two numbers are selected so that their XOR value is the largest,非常简单的 $trie$ 树板子题.这样就能拿到 $30pts$ 啦.

#include<bits/stdc++.h>
using namespace std;
#define in read()
#define MAXN 100100
#define MAXM MAXN << 2

inline int read(){
    
	int x = 0; char c = getchar();
	while(c < '0' or c > '9') c = getchar();
	while('0' <= c and c <= '9'){
    
		x = x * 10 + c - '0'; c = getchar();
	}
	return x;
}

int n = 0;
bool f1 = 1;
int tot = 0;
int first[MAXN] = {
     0 };
int   nxt[MAXM] = {
     0 };
int    to[MAXM] = {
     0 };
int   ans[MAXN] = {
     0 };
int   can[MAXN] = {
     0 };
inline void add(int x, int y){
    
	nxt[++tot] = first[x];
	first[x] = tot; to[tot] = y;
}

int dep[MAXN] = {
     0 };
int val[MAXN] = {
     0 };
int f[MAXN][50] = {
     0 };
void prework(int x, int fa){
    
	dep[x] = dep[fa] + 1, val[x] += val[fa];
	for(int i = 0; i <= 30; i++) f[x][i + 1] = f[f[x][i]][i];
	for(int e = first[x]; e; e = nxt[e]){
    
		int y = to[e];
		if(y == fa) continue;
		f[y][0] = x; prework(y, x);
	}
}

int Lca(int x, int y){
    
	if(dep[x] < dep[y]) swap(x, y);
	for(int i = 30; i >= 0; i--){
    
		if(dep[f[x][i]] >= dep[y]) x = f[x][i];
		if(x == y) return x;
	}
	for(int i = 30; i >= 0; i--)
		if(f[x][i] != f[y][i])
			x = f[x][i], y = f[y][i];
	return f[x][0]; 
}

int cnt = 0;
int trie[MAXN << 2][2] = {
     0 };

void add(int x){
    
	int p = 0;
	for(int i = 20; i >= 0; i--){
    
		int t = (x >> i) & 1;
		if(!trie[p][t])
			trie[p][t] = ++cnt;
		p = trie[p][t];
	}
}

int query(int x){
    
	int p = 0, ans = 0;
	for(int i = 20; i >= 0; i--){
    
		int t = (x >> i) & 1;
		if(trie[p][t ^ 1])
			p = trie[p][t ^ 1], ans += (1 << i);
		else p = trie[p][t];
	}
	return ans;
}

int main(){
    
// freopen("a.in", "r", stdin); 
	n = in;
	for(int i = 1; i < n; i++){
    
		int y = in;
		if(y != 1) f1 = 0;
		add(i + 1, y), add(y, i + 1);
	}
	for(int i = 1; i <= n; i++) val[i] = in;
	if(f1){
                                                        // ?栈?图 trie ???? 
		for(int i = 2; i <= n; i++) add(val[i] + val[1]);
		for(int i = 2; i <= n; i++) ans[1] = max(ans[1], query(val[i] + val[1]));
		cout << ans[1] << ' ';
		for(int i = 1; i < n; i++) cout << -1 << ' '; puts("");
	}
	else{
    
		prework(1, 0);
		for(int x = 1; x <= n; x++)
			for(int y = 1; y <= n; y++){
    
				if(x == y) continue;
				int lca = Lca(x, y);
				if(x == lca or y == lca) continue;
				int p = val[x] - val[f[lca][0]];
				int q = val[y] - val[f[lca][0]];
				ans[lca] = max(ans[lca], p ^ q), can[lca] = 1;
			}
		for(int i = 1; i <= n; i++)
			if(can[i]) cout << ans[i] << ' ';
			else cout << -1 << ' ';
		puts("");
	}
	return 0;
}

  The fourth point is also an extended chrysanthemum diagram,We found that contributions must be in two different subtrees,So we consider changing the way of joining.具体来说,对于一棵子树