当前位置:网站首页>凸函数的Hessian矩阵与高斯牛顿下降法增量矩阵半正定性的理解
凸函数的Hessian矩阵与高斯牛顿下降法增量矩阵半正定性的理解
2022-06-10 15:08:00 【知易行难wangshuailpp】
1.正定矩阵,半正定矩阵以及负定矩阵
矩阵所有特征值都大于零,则是正定矩阵
矩阵所有的特征值都不小于零,则是半正定矩阵
矩阵所有的特征值都小于零,则是负定矩阵
2.凸函数定义,海塞矩阵半正定性数学和几何意义
凸函数:任意属于定义域的两个自变量x1和x2,且对于任意0 =< a <= 1,如果函数f()满足f(a*x1+(1-a)) =< a*f(x1)+(1-a)f(x2),那么函数f()是凸函数。形象上的理解如下图所示,函数曲线上任意两点的连线一定在函数曲线的上方: 
多元函数的海塞矩阵半正定性就相当于一元函数二阶导非负性,因此凸函数的海塞矩阵一定是半正定。要想真正的理解凸函数海塞矩阵半正定性,需要从泰勒展开说起,
下式是一元函数泰勒二阶展开: 
如果函数f(x)是凸函数,那么必定当一阶导为零时,二阶导必须大于等于零,这样才满足f(x)存在极小值。
下式是多元函数泰勒展开,此时二阶导数变成了海塞矩阵: 
如果一阶导为0,是不是极小值完全取决于不同的dx, dy下,能不能做到最后一项一直非负。只有对于任意dx和dy,[dx,dy]H[dx,dy]T一直非负的情况,我们才能说这是极小值。如果一直非正,这就是极大值。如果它一会正一会负,就是鞍点。因此凸函数海塞矩阵是半正定矩阵。
3.高斯牛顿下降法中增量矩阵H半正定性
高斯牛顿法的实质也是用泰勒展开得到的,二次型来代替原函数,利用二次型的极值点的情况,逼近原函数的极值点。按照上面凸函数的推导,这里其实也是求一个极小值点,说白了也是一个凸函数的极值点。这里的增量矩阵就是凸函数的海塞矩阵。因此要满足高斯牛顿法有极小值点,必须要求增量矩阵半正定性。这里引用高翔视觉SLAM十四讲中内容,当增量矩阵为半正定型时,可能会出现奇异矩阵和病态的情况,此时增量的稳定性较差,因此高斯牛顿法要求增量矩阵为正定性,但实际情况下是半正定。
边栏推荐
- 100003 words, take you to decrypt the system architecture under the double 11 and 618 e-commerce promotion scenarios
- Scrollview is not at the top during initialization?
- 反“内卷”,消息称 360 企业安全云将上线“一键强制下班”功能,电脑自动关闭办公软件
- Ada Logics:CRI-O整体安全审计项目
- Interview question details
- Kubernetes 1.24: preventing unauthorized volume mode switching
- How to build a customer-centric product blueprint: suggestions from the chief technology officer
- rk3399_9.0去掉设置的一级菜单network & internet
- Jaeger引入了对OpenTelemetry的原生支持
- LeetCode_ 20 (brackets match)
猜你喜欢
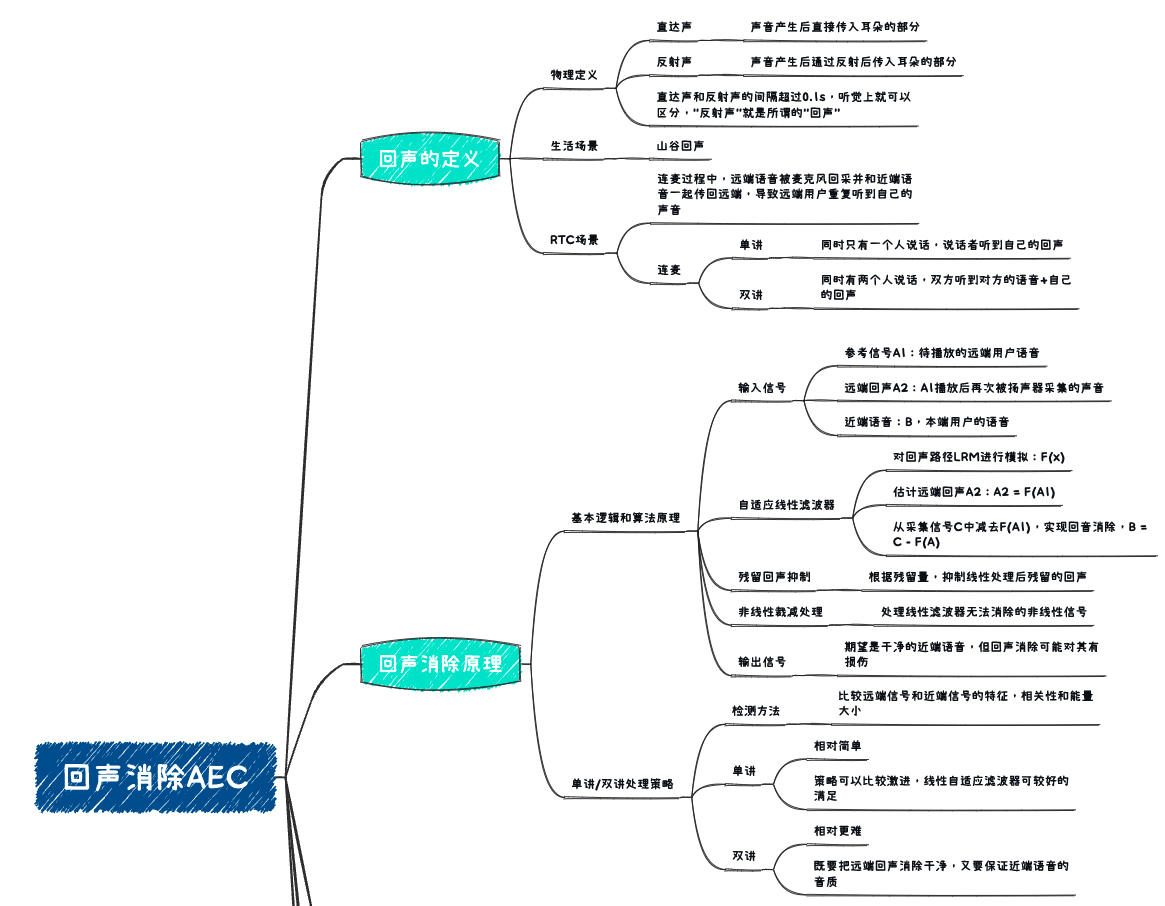
音视频处理三剑客之 AEC:回声产生原因及回声消除原理

CVPR 2022 oral | SCI: fast, flexible and robust low light image enhancement

4. Meet panuon again UI. Title bar of silver form

详解OpenCV的函数filter2D(),并提醒大家它做的运算并不是卷积运算而是相关运算

Using GDB to quickly read the kernel code of PostgreSQL

After class assignment for module 8 of phase 6 of the construction practice camp

In what scenario can we not use the arrow function?

Orgin framework notes

2022 the 15th Nanjing International Industrial Automation Exhibition

As a programmer, is it really that important for the underlying principles?
随机推荐
小程序网络请求Promise化
Orgin framework notes
JS中的call()方法和apply()方法用法总结
100003 words, take you to decrypt the system architecture under the double 11 and 618 e-commerce promotion scenarios
MITM(中间人攻击)
Overview of cann interface calling process
golang使用反射将一个结构体的数据直接复制到另一个结构体中(通过相同字段)
【Rust日报】2022-04-19 Rust异步框架的性能评估
Insight technology was selected into the "Aijian · privacy computing manufacturer panorama report" and was rated as a representative manufacturer of financial solutions
竟然还有人说ArrayList是2倍扩容,今天带你手撕ArrayList源码
We media video Hot Ideas sharing
4. Meet panuon again UI. Title bar of silver form
洞察的力量
在什么场景下,我们不能使用箭头函数?
Insight Technology a été sélectionné dans le rapport panorama des fournisseurs d'analyse de l'amour et d'informatique de la vie privée et a été évalué comme représentant des fournisseurs de solutions
New exploration of meta company | reduce Presto latency by using alluxio data cache
After class assignment for module 8 of phase 6 of the construction practice camp
Interview question details
CentOS Linux is dead! Oracle Linux may be a better alternative
2022第十五届南京国际数字化工业博览会