当前位置:网站首页>379. 捉迷藏
379. 捉迷藏
2022-06-24 19:42:00 【追寻远方的人】
Vani 和 cl2 在一片树林里捉迷藏。
这片树林里有 N 座房子,M 条有向道路,组成了一张有向无环图。
树林里的树非常茂密,足以遮挡视线,但是沿着道路望去,却是视野开阔。
如果从房子 A 沿着路走下去能够到达 B,那么在 A 和 B 里的人是能够相互望见的。
现在 cl2 要在这 N 座房子里选择 K 座作为藏身点,同时 Vani 也专挑 cl2 作为藏身点的房子进去寻找,为了避免被 Vani 看见,cl2 要求这 K 个藏身点的任意两个之间都没有路径相连。
为了让 Vani 更难找到自己,cl2 想知道最多能选出多少个藏身点。
输入格式
输入数据的第一行是两个整数 N 和 M。
接下来 M 行,每行两个整数 x,y,表示一条从 x 到 y 的有向道路。
输出格式
输出一个整数,表示最多能选取的藏身点个数。
数据范围
N≤200,M≤30000
输入样例:
7 5
1 2
3 2
2 4
4 5
4 6
输出样例:
3
思路:
/* 最小路径覆盖:针对一个有向无环图(DAG),用最少条互不相交路径,覆盖所有点。(其中互不相交是指点不重复) 结论:最小路径点覆盖(最小路径覆盖) = 总点数 - 最大匹配 证明: 1.建图 求最小路径覆盖用到拆点,一个点分成两个点,分别表示出点和入点, 那么从点i->j的一条边就用,从左边的出点i连到右边的入点j’表示, 于是得到的图是一个二分图,因为所有的边都是在左部和右部之间的,内部没有点。 2.转化 此时将原图中的每一条路径转化到新图中,因为原图中的路径互不相交,所以每一个点最多只有一个出度和入度, 这就意味着在新图中,左部每一个点最多只会向右部连一条边,右部的点最多只会有一条边连入,每个点最多只会属于一条边。 ①原图中的一条路径<=>新图中的一组匹配(新图中每一个点最多只会属于一条边) ②原图中每一条路径的终点(没有出边)<=>新图左部的非匹配点 3.推导 求原图中互不相交路径数<=>求路径终点数最少<=>求左部非匹配点最少<=>求最大匹配 拓展: 最小路径重复点覆盖:在最小路径覆盖问题的基础上,去掉互不相交。 结论:记原图G,求传递闭包后的图G’,则G的最小路径重复点覆盖=G’的最小路径覆盖 在该题中,记最小路径重复点覆盖数为cnt,该题的答案就是cnt 证明: ①k<=cnt 这cnt条路径覆盖了所有的点,所以所求的k个点一定要从这cnt条路径中的点选, 并且每条路径上最多选一个点,所以k<=cnt ②k>=cnt 构造:将cnt条路径的终点都放到一个集合E中,记next(E)返回的是从E中的每个点出发能到的所有点的集合 分类讨论: i)E ∩ next(E) = Ø ,此时E内的点不能相互到达,说明E中所有的点就是一种k=cnt的方案 ii)E ∩ next(E) ≠ Ø , 对于E中的任何一个点p,让这个点反向走,直到这个点走到一个不在next(E-p)中的点,可证当这个点走到起点时肯定不在next(E-p)中。 反证法:如果这个点走到起点,仍在next(E-p)中,说明p所在的路径的起点可以被其他路径到达,那么这条路径就没有存在的意义可以省去,不满足最小路径重复点覆盖。 所以此时同样可以在每一条路径中选出一个点,使得这些点之间两两不可到达,即k=cnt */
代码:
#include <cstdio>
#include <cstring>
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 210, M = 30010;
int n, m;
bool d[N][N], st[N];
int match[N];
bool find(int x)
{
for (int i = 1; i <= n; i ++ )
if (d[x][i] && !st[i])
{
st[i] = true;
int t = match[i];
if (t == 0 || find(t))
{
match[i] = x;
return true;
}
}
return false;
}
int main()
{
scanf("%d%d", &n, &m);
while (m -- )
{
int a, b;
scanf("%d%d", &a, &b);
d[a][b] = true;
}
// 传递闭包
for (int k = 1; k <= n; k ++ )
for (int i = 1; i <= n; i ++ )
for (int j = 1; j <= n; j ++ )
d[i][j] |= d[i][k] & d[k][j];
int res = 0;
for (int i = 1; i <= n; i ++ )
{
memset(st, 0, sizeof st);
if (find(i)) res ++ ;
}
printf("%d\n", n - res);
return 0;
}
边栏推荐
- Second IPO of Huafang group: grown up in Zanthoxylum bungeanum, trapped in Zanthoxylum bungeanum
- Selection (028) - what is the output of the following code?
- Theoretical analysis of countermeasure training: adaptive step size fast countermeasure training
- Laravel authentication module auth
- 01_ Getting started with the spingboot framework
- 伪原创智能改写api百度-收录良好
- RT-thread使用rt-kprintf
- Accounting standards for business enterprises application [5]
- 【js】-【数组应用】-学习笔记
- Record the range of data that MySQL update will lock
猜你喜欢

Dig deep into MySQL - resolve the clustered index / secondary index / federated index of InnoDB storage engine

【js】-【链表-应用】-学习笔记

01_SpingBoot 框架入门

InnoDB, the storage engine of MySQL Architecture Principle_ Redo log and binlog

03_ Spingboot core profile
Detailed explanation of online group chat and dating platform project (servlet implementation)

Tech talk activity review kubernetes skills of cloud native Devops
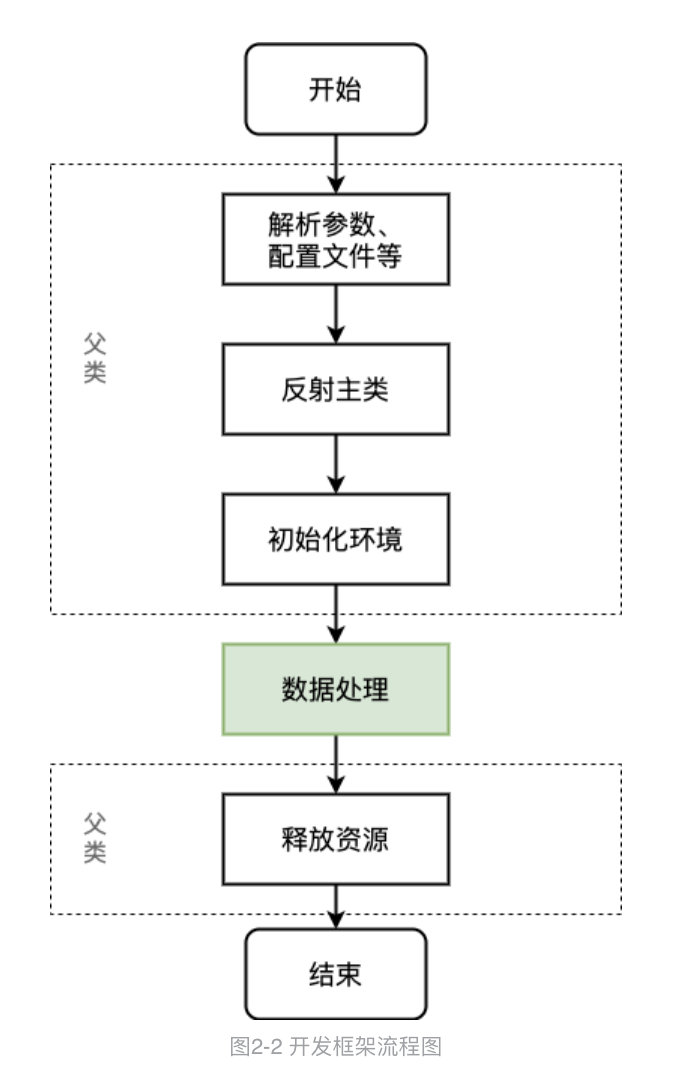
Spark 离线开发框架设计与实现

从客户端到服务器
07_SpingBoot 实现 RESTful 风格
随机推荐
【js】-【树】-学习笔记
How to add Google maps to a project
去处电脑桌面小箭头
Mycms we media CMS V3.0, resource push optimization, new free template
花房集团二次IPO:成于花椒,困于花椒
Construction equipment [5]
Laravel add helper file
How should we measure agile R & D projects?
力扣解法汇总515-在每个树行中找最大值
07_SpingBoot 实现 RESTful 风格
剑指 Offer 42. 连续子数组的最大和
非单文件组件
Accounting standards for business enterprises application [5]
02_SpingBoot 入门案例
Pousser l'information au format markdown vers le robot nail
【js】-【栈、队-应用】-学习笔记
Docker installation redis- simple without pit
laravel 创建 service层
Gocolly manual
Financial management [2]