leetcode 85. Max rectangle

Title Description ：

Given a contains only 0 and 1 、 The size is rows x cols Two dimensional binary matrix , Find out that only 1 The largest rectangle of , And return its area .
Example 1：

Input ：matrix = [[“1”,“0”,“1”,“0”,“0”],[“1”,“0”,“1”,“1”,“1”],[“1”,“1”,“1”,“1”,“1”],[“1”,“0”,“0”,“1”,“0”]]
Output ：6
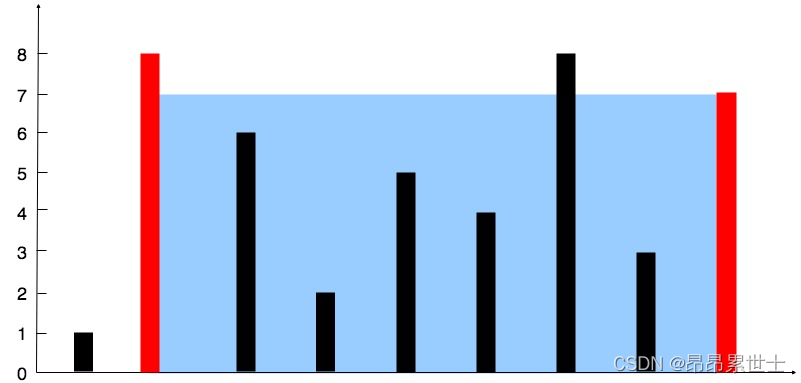
explain ： The largest rectangle is shown above .
Example 2：
Input ：matrix = []
Output ：0
Example 3：
Input ：matrix = [[“0”]]
Output ：0
Example 4：
Input ：matrix = [[“1”]]
Output ：1
Example 5：
Input ：matrix = [[“0”,“0”]]
Output ：0
Tips ：
rows == matrix.length
cols == matrix[0].length
1 <= row, cols <= 200
matrix[i][j] by ‘0’ or ‘1’

analysis

A very interesting question , This question is equivalent to leetcode 84. The largest rectangle in the histogram The extended application of this question .
First of all, we require that the matrix be all 1 The area of the largest rectangle in the submatrix of . Violence is to enumerate the coordinates of the upper left and lower right corners of a rectangle to determine a rectangle , The time complexity is O(n⁴), As for judging whether the rectangle is full 1, Using the two-dimensional prefix and, you can O（1） Within a period of time . Obviously, violent practices will TLE,n The scale is 200, If we can reduce the complexity to the cubic level , We can solve the problem . Since enumerating the two vertices of the rectangle will time out , Then the optimization direction can be to enumerate only one vertex , This is the same as in linear DP We often only need to find the optimal solution with a certain element as the end , Instead of enumerating the left and right endpoints to find the optimal solution . Therefore, we can only enumerate the vertices at the lower right corner of the rectangle , use f[i][j] Says to the first i Xing di j The column element is the largest area in the rectangle at the lower right corner of the rectangle .
Just to give you an example ：

0 1 1 1 1
0 1 0 1 1
1 1 1 1 1

We take the lower right corner of the matrix above as the lower right corner of the rectangle , Try to enumerate the widths of rectangles that can be formed , You can find that the last line has 5 A continuous 1, But it doesn't extend to the penultimate line , So the width is 5 The largest area of a rectangle is 5,. Then increase the height of the rectangle , Enumerate up , Because there are only two consecutive lines on the far right of the second line 1, So there are only two in the last line 1 Can continue to extend up , The new width is 2, It can be extended to the first line , So the width is 2 The largest area of a rectangle is 2 * 3 be equal to 6 了 .
Observe the above enumeration process , You can find , In enumerations, use matrix[i][j] When it is the rectangle at the lower right corner of the rectangle , How much width can be extended to the left depends on matrix[i][j] How many consecutive ones are there on the left 1, And when you increase the height of the rectangle , The width that can be extended upwards depends on the left 1 The least line , For example, the last floor has 5 individual 1, Because the rightmost part of the second floor is only 2 individual 1, The width of the rectangle has to be reduced to 2, Then go up if the left of the last column 1 If it continues to decrease , The width of the rectangle will continue to decrease , One of the attributes to be used all the time is how many elements are on the left side of a rectangle 1.
If the pretreatment comes out w[i][j] by matrix[i][j] And on page i Xing di j Column left continuous 1 The number of , Then the state transfer equation is w[i][j] = w[i][j-1] + 1,matrix[i][j] = 1 when ;w[i][j] = 0,matrix[i][j] = 0 when . With w[i][j] This attribute , We enumerate to matrix[i][j] Is the rectangle of the lower right vertex , You just need to enumerate the height of the rectangle up , Because the width is already held w The minimum value of . In this way, the complexity of the overall algorithm is reduced to the cubic level .

To observe the above , Our previous algorithm enumerates the last column , The maximum rectangular area with the last column of the third row as the lower right vertex of the rectangle is equal to max(5,2*3); The maximum rectangular area with the last column of the second row as the lower right vertex is equal to 2 * 2; The maximum rectangular area with the last column of the first row as the lower right vertex is equal to 4. The maximum area of the rectangle that can be formed in the lower right corner of this column is exactly the area of the largest rectangle in the histogram drawn in the above figure , That is, when we find the largest area of the rectangle in the lower right corner of a column of elements , We just need to find the abscissa of these elements , On the left 1 The number of is the maximum area of the rectangle in the histogram of the ordinate , That is to say, the same question at the beginning , Using the monotone stack, the enumeration time complexity of the area of a column of largest rectangles can be optimized to linear , The total complexity is on the square level . The maximum area of histogram can be referred to AcWing 131 The largest rectangle in the histogram This article explains .

Code

O(n³) Simulation solution

class Solution {
    
public:
    int w[205][205] = {
    0};
    int maximalRectangle(vector<vector<char>>& matrix) {
    
        int m = matrix.size(),n = matrix[0].size();
        for(int i = 0;i < m;i++){
    
            w[i][0] = (matrix[i][0] == '1');
            for(int j = 1;j < n;j++){
    
                if(matrix[i][j] == '1') w[i][j] = w[i][j-1] + 1;
            }
        }    
        int res = 0;
        for(int i = 0;i < m;i++){
    
            for(int j = 0;j < n;j++){
    
                int wid = w[i][j];
                for(int k = i;k >= 0&&wid;k--){
    
                    wid = min(wid,w[k][j]);
                    res = max(res,wid*(i - k + 1));
                }
            }
        }
        return res;
    }
};

O(n²) Monotone stack solution

class Solution {
    
public:
    int w[205][205] = {
    0};
    int maximalRectangle(vector<vector<char>>& matrix) {
    
        int m = matrix.size(),n = matrix[0].size();
        for(int i = 0;i < m;i++){
    
            w[i][0] = (matrix[i][0] == '1');
            for(int j = 1;j < n;j++){
    
                if(matrix[i][j] == '1') w[i][j] = w[i][j-1] + 1;
            }
        }    
        int res = 0;
        for(int j = 0;j < n;j++){
    
            vector<int> stk;
            vector<int> l(m+1,0);
            stk.push_back(-1);
            w[m][j] = -1;
            for(int i = 0;i <= m;i++){
    
                while(stk.size() > 1 && w[i][j] < w[stk.back()][j]){
    
                    int u = stk.back();
                    res = max(res,w[u][j]*(i - l[u] - 1));
                    stk.pop_back();
                }
                l[i] = stk.back();
                stk.push_back(i);
            }
        }
        return res;
    }
};