利用模 m 的原根存在性判断以及求解

一、题目：

模 m 的原根存在性判断以及求解。判断 m 原根是否存在，如存在给出一个原根以及所有原根。

二、问题描述

首先要判断给定模 m 是否存在原根，然后需要对其原根进行求解。

三、数学基础

• ① 埃氏筛法，将给定范围内的素数以打表的形式求解出来
• ② 判断是否存在原根
• ③ 对于给定模 m，求解欧拉函数 φ(m)
• ④ 利用欧几里德除法判断底数 a 和模 m 是否互素
• ⑤ 利用模平方重复法计算同余式的结果，判断是否同余 1

四、算法描述

• ① 埃氏筛法：先将大小为 n 的数组全部设置为 1，从 2 开始遍历该数组，遇到值为 1 的下标，便将其下标倍数的元素设置为 0（1 为素数，0 为合数）
• ② 判断给定模 m，原根存在性：模 m 是 2、4、pα、2pα 中的一种，才会存在原根
• ③ 求解欧拉函数，通过欧拉函数公式进行求解
• ④ 利用欧几里德除法判断互素：求解两个数的最大公因数，若最大公因数大于 1 则不互素，若最大公因数等于 1 则互素

⑤ 模平方重复法：此处算法实现方式为：answer 为模平方重复法中的 a，base 为 b，通过位运算将指数的二进制形式 and 1，加上二进制右移运算符，从而实现每次都对指数二进制最低位进行操作，实现二进制位的遍历。当二进制为 1 和 0 时，answer 和 base 有不同的求解方式。

五、算法实现

① 埃氏筛法：

void Eratosthenes(const int &num, vector<int> &prime)
{
    prime.resize(num + 1);
    for (auto &i : prime)
            = 1;
    prime[0] = 0, prime[1] = 0;
    for (int i = 1; i <= num + 1; ++i)
    {
        if (prime[i] == 0)
            continue;
//该数是素数，将他的倍数设置为合数
        int composite = i;
        while ((composite += i) <= num)
            prime[composite] = 0;
    }
}

② 判断原根存在性：

bool judge_exist_root(const int &num)
{
    if (num == 2 || num == 4)
        return true;
    Eratosthenes(num, prime);
    for (int element = 3; element < prime.size(); ++element)
    {
        if (prime[element] == 0)
            continue;
        for (int i = 1;; ++i)
        {
            int target = pow(element, i);
            if (target > num)
                break;
            if (target == num || target * 2 == num)
                return true;
        }
    }
    return false;
}

③ 欧拉函数：

int Euler(const int &num)
{
//求欧拉函数
    if (prime[num] == 1)
        return num - 1;
    int result = num, n = num;
    for (int i = 2; i * i <= n; ++i)
    {
        if (n % i == 0)
        {
//找到一个素因子
            result = result / i * (i - 1);
            while (n % i == 0)
//将该素因子全部约去
                /= i;
        }
    }
    if (n > 1)
//检验有无遗漏
        result = result / n * (n - 1);
    return result;
}

④ 判断两个数是否互素：

bool coprime(int i, int num)
{
//欧几里德除法判断互素
    if (i == 1 || num == 1)
// 两个正整数中，只有其中一个数值为1，两个正整数为互质数
        return true;
    while (1)
    {
//求出两个数的最大公约数
        int temp = i % num;
        if (temp == 0)
            break;
        else
                = num, num = temp;
    }
    if (num > 1)
// 如果最大公约数大于1，表示两个正整数不互质
        return false;
    return true;
}

⑤ 模平方重复法：

int quick_pow(const int &a, int b, const int &mod)
{
//模平方重复法
    int answer = 1, base = a % mod; //answer为模平方重复法中的a，base为b
    while (b != 0)
    {
//位运算and，计算结果为a的二进制最低一位是否为1,通过右移运算符更新最低位
        if (b & 1)
            answer = (answer * base) % mod;
        base = (base * base) % mod;
        >>= 1;
    }
    return answer;
}

六、运行结果

输入我需要的数据范围上限，给定 41，就会在测试用例中生成 3~41 的所有数

生成测试用例

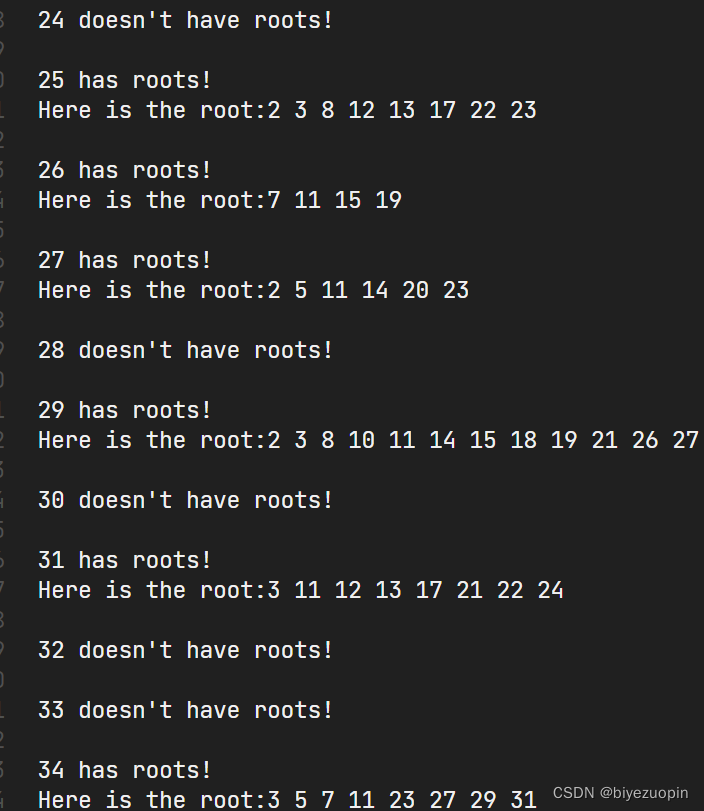
结果保存在另一个 result.txt 文件中