当前位置:网站首页>Principles of permutation entropy, fuzzy entropy, approximate entropy, sample entropy and approximate entropy implemented by MATLAB
Principles of permutation entropy, fuzzy entropy, approximate entropy, sample entropy and approximate entropy implemented by MATLAB
2022-08-02 16:32:00 【智赵】
说明:“This blog post is about permutation entropy、模糊熵、近似熵、The principle of sample entropy andMATLAB实现”The last in a series of blog posts,About permutation entropy、模糊熵、Please read the blog for the content of sample entropy:
四、近似熵
1.简介
近似熵(approximate entropy,ApEn)The complexity of time series can be quantitatively described,序列的复杂性越大,相应的近似熵也越大.The value of approximate entropy is less affected by the amount of data,for non-stationary、The quantization results of nonlinear sequences are stable,It is widely used in practical engineering.
2.基本原理
设有长度为 N N N 的时间序列 X = [ x 1 , x 2 , … , x N ] X= [x_{1}, x_{2},…,x_{N} ] X=[x1,x2,…,xN],The calculation steps of its approximate entropy are as follows:
Step1:将时间序列 X X X The elements are in order to have m m m 维数的向量,即
X i = [ x ( i ) , x ( i + 1 ) , . . . , x ( i + m − 1 ) ] X_{i}=[x(i),x(i+1),...,x(i+m-1)] Xi=[x(i),x(i+1),...,x(i+m−1)]
式中, i = 1 , 2 , … , N − m + 1 i=1, 2 , … , N-m+1 i=1,2,…,N−m+1.
Step2:定义 d [ X i , X j ] d [X_{i}, X_{j}] d[Xi,Xj] 为向量 X i X_{i} Xi 与 X j X_{j} Xj 的距离,则:
d [ X i , X j ] = m a x ∣ x ( i + k ) − x ( j + k ) ∣ , k ∈ ( 0 , m − 1 ) d [X_{i}, X_{j}]=max|x(i+k)-x(j+k)|,k∈(0,m-1) d[Xi,Xj]=max∣x(i+k)−x(j+k)∣,k∈(0,m−1)
Step3:记 B i B_{i} Bi 为 d [ X i , X j ] ≤ r d [X_{i}, X_{j}] ≤ r d[Xi,Xj]≤r的个数( r r r for similar tolerances),并计算 B i B_{i} Bi with all vector numbers N − m + 1 N-m+1 N−m+1 的比值,即:
B i m ( r ) = B i N − m + 1 B^{m}_{i}(r)=\frac{B_{i}}{N-m+1} Bim(r)=N−m+1Bi
Step4:对 B i m ( r ) B^{m}_{i}(r) Bim(r) Perform a logarithmic operation,再求其对所有 i i i 的平均值,记作 B m ( r ) B^{m}(r) Bm(r) ,则有:
B m ( r ) = 1 N − m + 1 ∑ i = 1 N − m + 1 l n B i m ( r ) B^{m}(r)=\frac{1}{N-m+1}\sum_{i=1}^{N-m+1}lnB^{m}_{i}(r) Bm(r)=N−m+11i=1∑N−m+1lnBim(r)
Step5:令 m = m + 1 m=m+1 m=m+1,并重复 Step1~Step4,即可得到 B m + 1 ( r ) B^{m+1}(r) Bm+1(r) .
Step6:理论上,The approximate entropy of this sequence is :
A p E n ( m , r ) = l i m [ B m ( r ) − B m + 1 ( r ) ] , N → ∞ ApEn(m,r)=lim[B^{m}(r)-B^{m+1}(r)],N→∞ ApEn(m,r)=lim[Bm(r)−Bm+1(r)],N→∞
for the actual sequence, N N N cannot approach infinity,So the approximate entropy can be expressed as :
A p E n ( m , r , N ) = B m ( r ) − B m + 1 ( r ) ApEn(m,r,N)=B^{m}(r)-B^{m+1}(r) ApEn(m,r,N)=Bm(r)−Bm+1(r)
Approximate entropy is essentially a statistic about sequences and parameters,Its size and data length N N N 、嵌入维数 m m m and similar tolerances r r r 有关.In order to obtain better statistical properties and smaller errors, 数据长度 N N N 通常在100~5000 取值,嵌入维数 m m m 一般取 1 或 2,相似容限 r r r 取(0.1~0.25)* s t d std std, s t d std std is the standard deviation of the series.
3.MATLAB代码
% 主程序
clc;
clear;
close all;
%% 产生仿真信号
fs = 1000; % 数据采样率
t = (0:1/fs:(1-1/fs)); % 时间
x = cos(50*pi*t+sin(5*pi*t)); % 数据
%% 画图
figure;
plot(t,x);
xlabel('t/s');ylabel('幅值');title('信号的时域波形');
%% Find the simulated signalx的近似熵
m = 2; % 嵌入维数
r0 = 0.2; % Coefficients of similar tolerances
r = r0*std(x); % 相似容限
appEn = ApproximateEntropy(m,r,x); % 近似熵
% Find a function of approximate entropy
function appEn = ApproximateEntropy(dim, r, data, tau)
% The author of the approximate entropy algorithm:Pincus S M . Approximate entropy as a measure of system complexity[J]. Proceedings of the National Academy of Sciences ,1991,88(6):2297—2301.
% Input:
% dim:嵌入维数(一般取1或者2)
% r:相似容限( 通常取0.1*Std(data)~0.25*Std(data) )
% data:时间序列数据,data须为1xN的矩阵
% tau:Downsampling delay time(The default value is 1的情况下,User can ignore this item)
% Output:
% appEn:Approximate entropy of the requested data
if nargin < 4
tau = 1;
end
if tau > 1
data = downsample(data, tau);
end
N = length(data);
result = zeros(1,2);
for m = dim:dim+1
Bi = zeros(N-m+1,1);
dataMat = zeros(N-m+1,m);
% Set up the data matrix,构造成m维的矢量
for i = 1:N-m+1
dataMat(i,:) = data(1,i:i+m-1);
end
% Calculate the number of similar patterns using distance
for j = 1:N-m+1
% 计算切比雪夫距离,Including self-matching cases
dist = max(abs(dataMat - repmat(dataMat(j,:),N-m+1,1)),[],2);
% 统计dist小于等于r的数目
D = (dist <= r);
% Including self-matching cases
Bi(j,1) = sum(D)/(N-m+1);
end
% 求所有Bi的均值
result(m-dim+1) = sum(log(Bi))/(N-m+1);
end
% Calculated approximate entropy value
appEn = result(1)-result(2);
end
参考文献
[1] 近似熵理论相关知识与代码实现
[2] Pincus S M . Approximate entropy as a measure of system complexity[J]. Proceedings of the National Academy of Sciences ,1991,88(6):2297—2301.
边栏推荐
猜你喜欢
随机推荐
个人成长系列:好问题清单
JVM常量池详解
【无标题】
webrtc 数据接收流程图解
abstract和接口的基础知识
Oauth2.0 authentication server adds verification code login method
Oauth2.0 authentication server construction
UINIX 高级环境编程杂项之限制
大厂年薪50w+招聘具有测试平台开发能力的测试工程师
RouteOS 导入至PVE
【软件测试】项目中关于测试人员的简单介绍
Mediasoup 杂谈(待完善)
网络运维系列:网络出口IP地址查询
Zabbix: PHP option“date.timezone” Fail
Priority table and Ascll table
Oauth2.0 security (take WeChat authorized login as an example)
解决跨域问题的方法 --- JSONP
【软件测试】selenium自动化测试1
Scala的安装和IDEA的使用(初入茅庐)
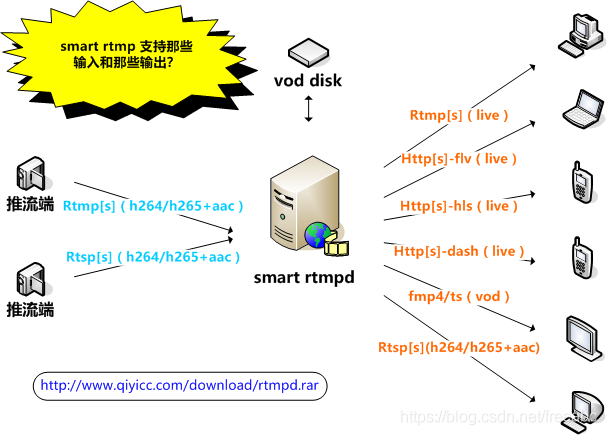
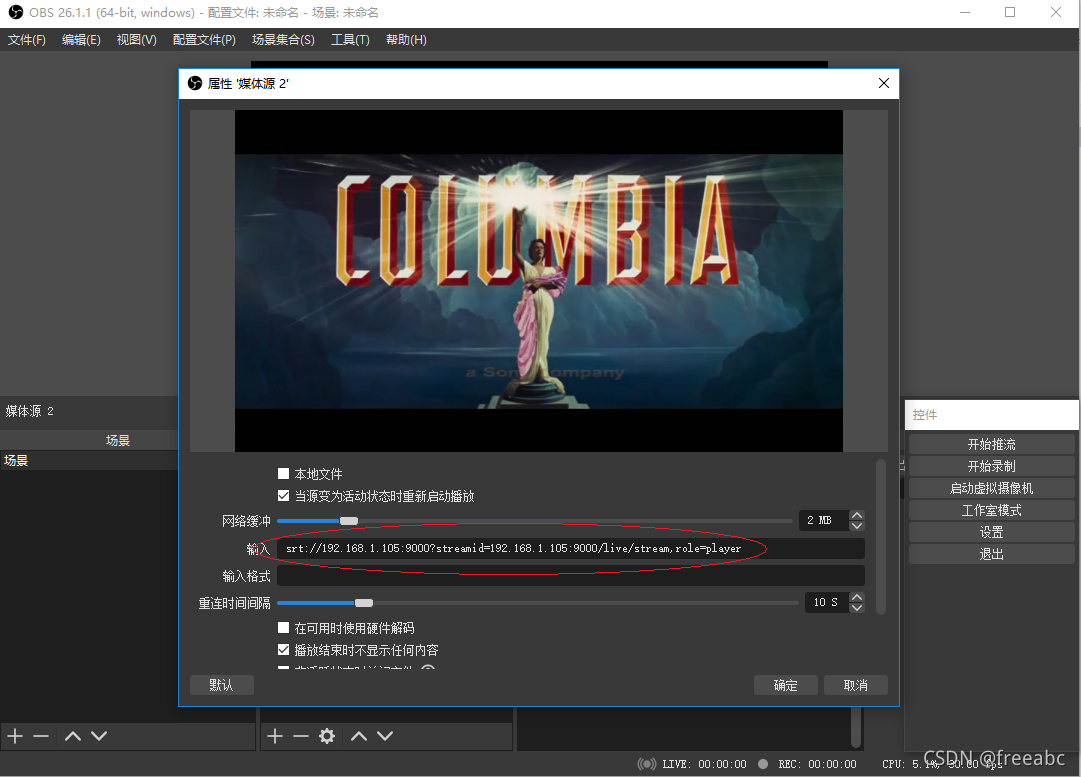
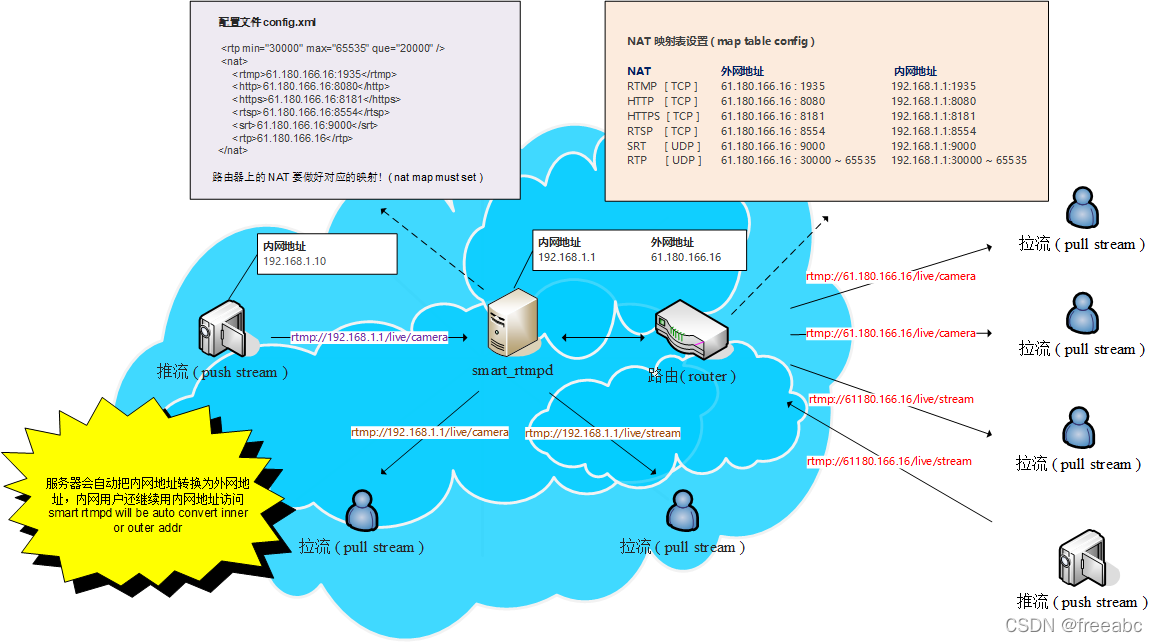
smart_rtmpd 的 NAT 映射方式使用说明