当前位置:网站首页>Leetcode (406) - rebuild the queue based on height
Leetcode (406) - rebuild the queue based on height
2022-06-28 14:30:00 【SmileGuy17】
Leetcode(406)—— Rebuild the queue according to height
subject
Let's say there's a group of people in a disordered order standing in a line , Array p e o p l e people people Properties that represent some people in the queue ( Not necessarily in order ). Every p e o p l e [ i ] = [ h i , k i ] people[i] = [hi, ki] people[i]=[hi,ki] It means the first one i i i The height of an individual is h i hi hi, front Just right Yes ki Height greater than or equal to hi People who .
Please reconstruct and return the input array p e o p l e people people The queue represented by . The returned queue should be formatted as an array q u e u e queue queue, among q u e u e [ j ] = [ h j , k j ] queue[j] = [hj, kj] queue[j]=[hj,kj] It's number one in the queue j j j Personal attributes ( q u e u e [ 0 ] queue[0] queue[0] It's the people at the front of the line ).
Example 1:
Input :people = [[7,0],[4,4],[7,1],[5,0],[6,1],[5,2]]
Output :[[5,0],[7,0],[5,2],[6,1],[4,4],[7,1]]
explain :
The number is 0 The height of a person who is 5 , No one is taller or the same in front of him .
The number is 1 The height of a person who is 7 , No one is taller or the same in front of him .
The number is 2 The height of a person who is 5 , Yes 2 A taller or the same person is in front of him , That is, the number is 0 and 1 People who .
The number is 3 The height of a person who is 6 , Yes 1 A taller or the same person is in front of him , That is, the number is 1 People who .
The number is 4 The height of a person who is 4 , Yes 4 A taller or the same person is in front of him , That is, the number is 0、1、2、3 People who .
The number is 5 The height of a person who is 7 , Yes 1 A taller or the same person is in front of him , That is, the number is 1 People who .
therefore [[5,0],[7,0],[5,2],[6,1],[4,4],[7,1]] It's the reconstructed queue .
Example 2:
Input :people = [[6,0],[5,0],[4,0],[3,2],[2,2],[1,4]]
Output :[[4,0],[5,0],[2,2],[3,2],[1,4],[6,0]]
Tips :
- 1 1 1 <= people.length <= 2000 2000 2000
- 0 0 0 <= hi <= 1 0 6 10^6 106
- 0 0 0 <= ki < people.length
- The topic data ensures that the queue can be rebuilt
Answer key
Method 1 : greedy ( Sort from high to low + Insert )
Ideas
similarly , We can also sort everyone according to their height , People of the same height are treated in a similar way , namely : according to h i h_i hi In descending order for the first keyword , k i k_i ki Sort the second keyword in ascending order . If we follow the order after the order , Put everyone in the queue in turn , that When we put in the i i i Personal time :
- The first 0 , ⋯ , i − 1 0, \cdots, i-1 0,⋯,i−1 Tall people have been placed in the queue , They just stand on the i i i Personal front , It'll be right i i i Personal influence , Because they are better than i i i Personal height ;
- And the first i + 1 , ⋯ , n − 1 i+1, \cdots, n-1 i+1,⋯,n−1 Tall people haven't been put in the queue yet , And wherever they stand , Right. i i i There is no personal impact , Because they are better than i i i Personal short .
under these circumstances , We don't know how many should be arranged for the people behind us 「 empty 」 Location , Therefore, method 2 cannot be used . But we can see , Since the people behind won't be right i i i Personal impact , We can use 「 Insert empty 」 Methods , Select an insertion position for each person in the current queue in turn . in other words , When we put in the i i i Personal time , Just insert it into the queue , So that there happened to be k i k_i ki Just a person .
Code implementation
class Solution {
public:
vector<vector<int>> reconstructQueue(vector<vector<int>>& people) {
// current people Not necessarily in order , We need to reorder , Achieve the following requirements :
// Every people[i] = [hi, ki] It means the first one i The height of an individual is hi , front Just right Yes ki Height greater than or equal to hi People who
// Sort from the back ? It might be better . It would be better to choose from high to low ? try
// Sort ,people[n][0] The big one is in front ,people[n][0] Phase at the same time people[n][1] The small one is in the front
sort(people.begin(), people.end(),
[](vector<int>& A, vector<int>& B){
if(A[0] == B[0]) return A[1] < B[1];
else return A[0] > B[0];
});
vector<vector<int>> ans;
int size = people.size();
for(int n = 0; n < size; n++){
// Every time a new value is inserted , Because according to people[0] Insert from large to small , At this time in ans The number in is greater than or equal to it
// So according to people[1] Select the number of rows , For example 0 when , There is no value greater than or equal to it , And because at this time ans The number in is greater than or equal to it
// So it's inserted first
if(ans.empty()) ans.push_back(people[n]);
else ans.insert(ans.begin()+people[n][1], people[n]);
}
return ans;
}
};
Complexity analysis
Time complexity : O ( n 2 ) O(n^2) O(n2), among n n n It's an array people \textit{people} people The length of . We need to O ( n log n ) O(n \log n) O(nlogn) Time to sort , Then you need to O ( n 2 ) O(n^2) O(n2) Time to traverse each person and put them in the queue . Because the former is smaller than the latter in the asymptotic sense , So the total time complexity is O ( n 2 ) O(n^2) O(n2).
Spatial complexity : O ( log n ) O(\log n) O(logn), This is the stack space needed for sorting .
Method 2 : greedy ( Sort from low to high + establish )
Ideas
When everyone's height is different , If we sort them by height from small to large , Then you can easily restore the original queue .
For narrative purposes , We set the number of people as n n n, After sorting , Their height is in order of h 0 , h 1 , ⋯ , h n − 1 h_0, h_1, \cdots, h_{n-1} h0,h1,⋯,hn−1, And ranked No i i i The height in front of an individual is greater than h i h_i hi The number of people is k i k_i ki. If we follow the order after the order , Put everyone in the queue in turn , that When we put in the i i i Personal time :
- The first 0 , ⋯ , i − 1 0, \cdots, i-1 0,⋯,i−1 The short man has been placed in the queue , And wherever they stand , Right. i i i There is no personal impact , Because they are better than i i i Personal short ;
- And the first i + 1 , ⋯ , n − 1 i+1, \cdots, n-1 i+1,⋯,n−1 The short man hasn't been put in the queue yet , But as long as they stand on the i i i Personal front , It'll be right i i i Personal influence , Because they are better than i i i Personal height .
If we Create an initial containing n n n Empty queue of locations , And every time we put a person in the queue , It will 「 empty 」 The position becomes 「 full 」 Location , that When we put in the i i i Personal time , We need to arrange one for him 「 empty 」 Location , And this 「 empty 」 Just in front of the position is k i k_i ki individual 「 empty 」 Location , It is used to arrange for the taller people behind . in other words , The first i i i Personal position , It is the number from left to right in the queue k i + 1 k_i+1 ki+1 individual 「 empty 」 Location .
So if someone of the same height , Above k i k_i ki Greater than in the definition is not equivalent to greater than or equal to that required in the topic description , At this point, how to modify the above method ? We can think of it this way , If the first i i i The individual and the third j j j Individuals of the same height , namely h i = h j h_i = h_j hi=hj, Then we can reduce the height of the person in the lower position in the queue a little . let me put it another way , For a certain height value h h h, We will rank the first one in the queue as h h h The people remain the same , The second one is h h h The height of the people decreased δ \delta δ, The third is h h h The height of the people decreased 2 δ 2\delta 2δ, And so on , among δ \delta δ It's a very small constant , It makes any height h h h People will not be with others ( Height is not h h h Of ) Man made influence .
How to find the first 、 the second 、 The third is h h h What about the people ? We can use k k k value , You can find : When h i = h j h_i=h_j hi=hj when , If k i > k j k_i > k_j ki>kj, It means that i i i Must be relative to j j j At a later position in the queue ( Because in the first place j j j Everyone who was taller than him before , Must be better than i i i One should be tall ), According to the modified results , h i h_i hi slightly smaller than h j h_j hj, The first i i i Individuals should be ranked before j j j Individuals are put in a queue . therefore , We You don't really have to change your height , And just follow h i h_i hi Ascending order for the first keyword , k i k_i ki Sort the second keyword in descending order . here , People of the same height are arranged in reverse order according to their positions in the queue , This indirectly reduces the height δ \delta δ The effect of this operation .
thus , We just need to use the method mentioned at the beginning , Will be the first i i i The first person in the queue k i + 1 k_i+1 ki+1 Empty space , You can get the original queue .
Code implementation
class Solution {
public:
vector<vector<int>> reconstructQueue(vector<vector<int>>& people) {
// Sort ,people[n][0] The small one is in the front ,people[n][0] Phase at the same time people[n][1] The big one is in front
sort(people.begin(), people.end(), [](vector<int>& A, vector<int>& B){
if(A[0] == B[0]) return A[1] > B[1];
else return A[0] < B[0];
});
int size = people.size();
int space;
vector<vector<int>> ans(size);
for(int n = 0; n < size; n++){
space = people[n][1];
for(int i = 0; i < size; i++){
if(ans[i].empty()) space--;
if(space < 0){
ans[i].insert(ans[i].end(), {
people[n][0], people[n][1]});
break;
}
}
}
return ans;
}
};
Complexity analysis
Time complexity : O ( n 2 ) O(n^2) O(n2), among n n n It's an array people \textit{people} people The length of . We need to O ( n log n ) O(n \log n) O(nlogn) Time to sort , Then you need to O ( n 2 ) O(n^2) O(n2) Time to traverse each person and put them in the queue . Because the former is smaller than the latter in the asymptotic sense , So the total time complexity is O ( n 2 ) O(n^2) O(n2).
Spatial complexity : O ( log n ) O(\log n) O(logn), This is the stack space needed for sorting .
边栏推荐
猜你喜欢

Talking from the little nematode -- tracing the evolution of nervous system and starting life simulation

Mulan open work license 1.0 open to the public for comments
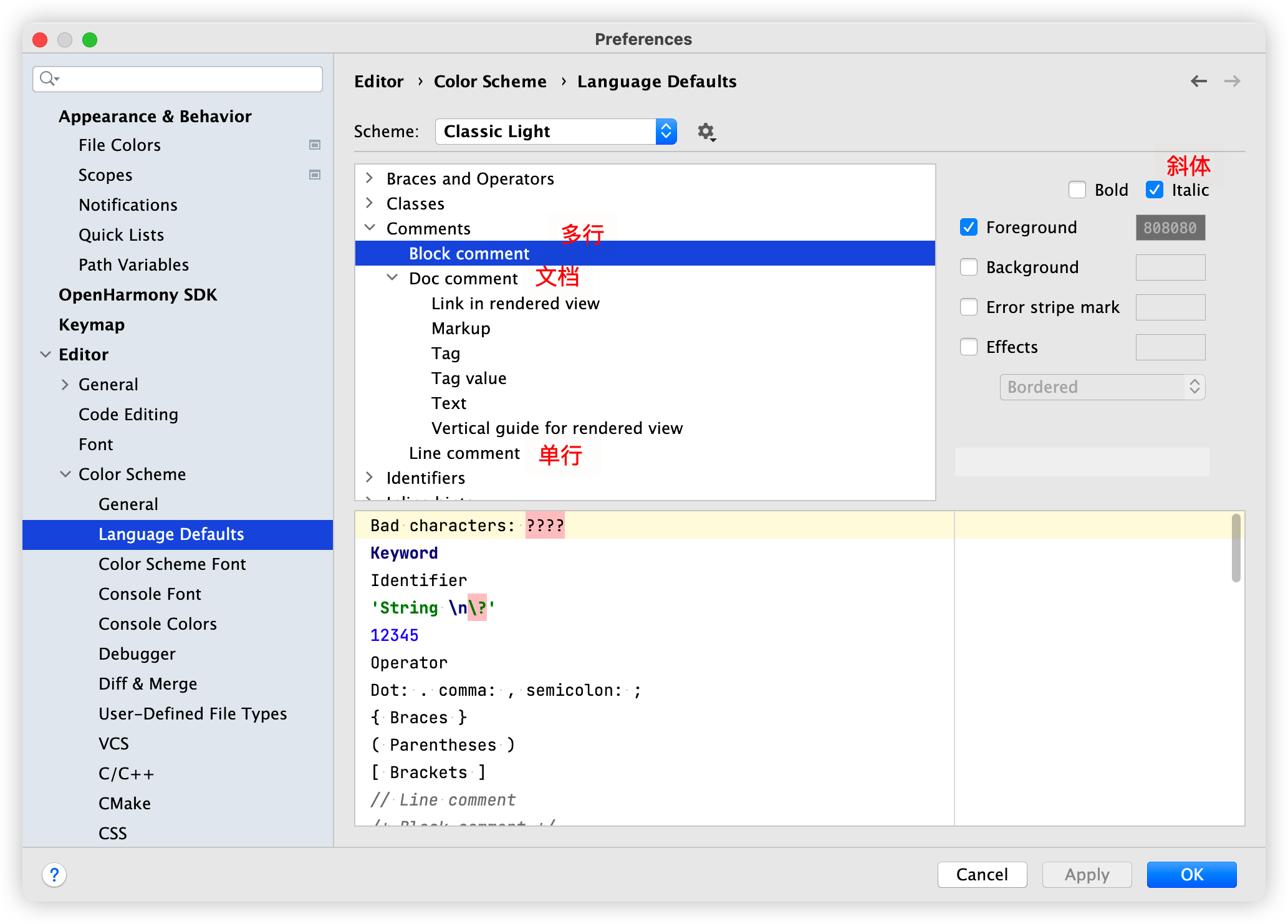
Deveco studio 3.0 editor configuration tips

运行近20年,基于Win 98的火星探测器软件迎来首次升级

荐书丨《大脑通信员》:如果爱情只是化学反应,那还能相信爱情吗?

基于 Nebula Graph 构建百亿关系知识图谱实践

PC Museum - familiar and strange ignorant age

坐拥755万开发者的中国开源,进度几何?

Flutter series: offstage in flutter

你的代碼會說話嗎?(上)
随机推荐
What is the progress of China open source with 7.55 million developers?
Dry goods | how to calculate the KPI of scientific researchers, and what are the h index and G index
验证回文串
Introduction to common components of IOT low code platform
IonQ联合GE Research证实:量子计算在风险聚合上有巨大潜力
Which securities company is the largest and safest? How to open an account is the safest
openGauss内核:SQL解析过程分析
Connected to rainwater series problems
GPS数据格式的分析与处理[通俗易懂]
Rslo: self supervised lidar odometer (real time + high precision, icra2022)
js 判断字符串为空或者不为空
i++ , ++i
开源社邀您参加OpenInfra Days China 2022,议题征集进行中~
外贸邮件推广怎么统计维度
2022下半年软考考试时间安排已确定!
Single responsibility principle
2022中式烹調師(高級)試題及在線模擬考試
Foreign trade SEO Webmaster Tools
由两个栈组成的队列
2022年焊工(技师)考试题库模拟考试平台操作