当前位置:网站首页>Self control principle learning notes - system stability analysis (1) - BIBO stability and Routh criterion
Self control principle learning notes - system stability analysis (1) - BIBO stability and Routh criterion
2022-07-27 19:03:00 【Miracle Fan】
Self control principle learning notes
Self control principle learning notes column
1. The input and output are stable - about CLTIS
1.1 Two steady states
1.1.1 BIBO Stable
Definition : If a system is subjected to a bounded input or disturbance, its response is finite .
necessary and sufficient condition :
y ( t ) = ∫ 0 t g ( τ ) u ( t − τ ) d τ ⇒ ∣ y ( t ) ∣ ≤ ∫ 0 t ∣ g ( τ ) ∣ ⋅ ∣ u ( t − τ ) ∣ d τ ≤ M ∫ 0 t ∣ g ( τ ) ∣ d τ y(t)=\int_0^tg(\tau)u(t-\tau)d\tau\Rightarrow |y(t)|\le \int _0^t|g(\tau)|\cdot |u(t-\tau)|d\tau \le M\int_0^t|g(\tau)|d\tau y(t)=∫0tg(τ)u(t−τ)dτ⇒∣y(t)∣≤∫0t∣g(τ)∣⋅∣u(t−τ)∣dτ≤M∫0t∣g(τ)∣dτ
If you want to make y(t) bounded , Then the necessary and sufficient condition is ∣ g ( τ ) ∣ |g(\tau)| ∣g(τ)∣ Absolutely integrableNon integrable examples : g ( t ) = 1 t − 1 g(t)=\frac{1}{t-1} g(t)=t−11
about CLTIS, Satisfy BIBO Then there is only the pole of the left half plane :
Assume that the transfer function is impulse response Laplace Transformation , therefore :
G ( s ) = ∫ 0 ∞ g ( t ) e − s t d t ⇒ ∣ G ( s ) ∣ ≤ ∫ 0 ∞ ∣ g ( t ) ∣ ⋅ ∣ e − s t ∣ d t = ∫ 0 ∞ ∣ g ( t ) ∣ ⋅ ∣ e − σ t ∣ d t * i f σ ≥ 0 , ∣ G ( s ) ∣ ∣ s = σ + i w → ∞ ≤ ∫ 0 ∞ ∣ g ( t ) ∣ ⋅ ∣ e − σ t ∣ d t ≤ ∫ 0 ∞ ∣ g ( t ) ∣ d t G(s)=\int_0^\infty g(t)e^{-st}dt\Rightarrow|G(s)|\le\int_0^\infty |g(t)|\cdot|e^{-st}|dt=\int_0^\infty|g(t)|\cdot|e^{-\sigma t}|dt\\ \Longrightarrow if \quad\sigma \ge 0,\quad |G(s)||_{s=\sigma+iw}\rightarrow\infty\le\int^\infty_0|g(t)|\cdot|e^{-\sigma t}|dt\le\int_0^\infty|g(t)|dt G(s)=∫0∞g(t)e−stdt⇒∣G(s)∣≤∫0∞∣g(t)∣⋅∣e−st∣dt=∫0∞∣g(t)∣⋅∣e−σt∣dt*ifσ≥0,∣G(s)∣∣s=σ+iw→∞≤∫0∞∣g(t)∣⋅∣e−σt∣dt≤∫0∞∣g(t)∣dt
∣ g ( t ) ∣ |g(t)| ∣g(t)∣ unbounded , And BIBO Stabilize contradictions , All only when σ < 0 \sigma<0 σ<0, Meet the conditions .
1.1.2 Zero input stability ( Asymptotic stability )
- Definition : When t It goes to infinity , The response produced by the initial conditions tends to 0.
- Sufficient and necessary conditions for stability :
- about ∀ s i , R e ( s i ) < 0 when , C L T I S gradually near steady set \forall s_i,Re(s_i)<0 when ,CLTIS Asymptotic stability ∀si,Re(si)<0 when ,CLTIS gradually near steady set
- R e ( s i ) > 0 ∣ ∣ There are multiple virtual roots , C L T I S No steady set Re(s_i)>0||\text{ There are multiple virtual roots },CLTIS unstable Re(si)>0∣∣ There are multiple virtual roots ,CLTIS No steady set
- There are only single virtual roots , other R e ( s j ) < 0 Re(s_j)<0 Re(sj)<0,LTIS Critical delimitation .
- Related examples :
1.1.3 Stability related instructions
- about LTIS,BIBO、 Zero input stability requires eigenvalues to be located on the left of the complex plane
- about LTIS, Stability only depends on the inherent properties of the system ( The eigenvalue ), It has nothing to do with external conditions .
- Stability has a local characteristic ( Multiple stable points ), But only in time-varying systems and nonlinear systems , Time invariant systems are global .
2. Routh-Hurwitz The criterion
2.1 CLTIS Necessary conditions for stability
All coefficients of the characteristic equation of the system are greater than 0
2.2 Routh The criterion
List some Routh surface
s n a n a n − 2 a n − 4 … s^n\quad a_n \quad a_{n-2}\quad a_{n-4} \quad \dots snanan−2an−4…
s n − 1 a n − 1 a n − 3 a n − 5 … s^{n-1}\quad a_{n-1} \quad a_{n-3}\quad a_{n-5} \quad \dots sn−1an−1an−3an−5…
s n − 2 b 1 b 2 b 3 … s^{n-2}\quad b_1 \quad b_2\quad b_3 \dots sn−2b1b2b3…
s n − 3 c 1 c 2 … s^{n-3}\quad c_1 \quad c_2\quad \dots sn−3c1c2…
…………
s 0 h 1 s^0 \quad h_1 s0h1
Conventional calculation
b 1 = − [ a n a n − 2 a n − 1 a n − 3 ] a n − 1 b 2 = − [ a n a n − 4 a n − 1 a n − 5 ] a n − 1 c 1 = − [ a n − 1 a n − 3 b 1 b 2 ] b 1 c 2 = − [ a n − 1 a n − 5 b 1 b 3 ] b 1 b_1=-\frac{ \begin{bmatrix} a_{n}& a_{n-2} \\ a_{n-1}& a_{n-3} \end{bmatrix} } {a_{n-1}} \quad b_2=-\frac{ \begin{bmatrix} a_{n}& a_{n-4} \\ a_{n-1}& a_{n-5} \end{bmatrix} } {a_{n-1}}\\ c_1=-\frac{ \begin{bmatrix} a_{n-1}& a_{n-3} \\ b_1&b_2 \end{bmatrix} } {b_1} \quad c_2=-\frac{ \begin{bmatrix} a_{n-1}& a_{n-5} \\ b_1&b_3 \end{bmatrix} } {b_1} b1=−an−1[anan−1an−2an−3]b2=−an−1[anan−1an−4an−5]c1=−b1[an−1b1an−3b2]c2=−b1[an−1b1an−5b3]Judge the stability method :
The number of changes of the coefficient symbol in the first column , That is, the characteristic root is in the right half s Number of planes
Necessary and sufficient conditions for stability : The coefficients in the first column of the table are all greater than 0
2.3 Related applications
(1) The first column coefficient is 0
Use small ϵ \epsilon ϵ Method instead of zero value term , Continue to solve according to the conventional method .
If the first column is all positive , The system is not asymptotically stable , But there are pure virtual roots , Critical stability
(2) The coefficients of a row are all 0
indicate s The plane has a real root symmetrical to the origin , Or conjugate virtual root
- Take all as 0 Previous line of , Take its coefficient as the auxiliary equation ( Only take even times )
- Derivation of auxiliary equation , The coefficient substitution is 0 That's ok
- Continue with the normal steps
- Solve the auxiliary equation to get the symmetric root
(3) Related stability problems
Use the idea of exchange .
If the realistic part is less than 2, Then set u=s+2 Put it into the equation , take u As an equation variable , To solve the .
2.4 Hurwitz The criterion
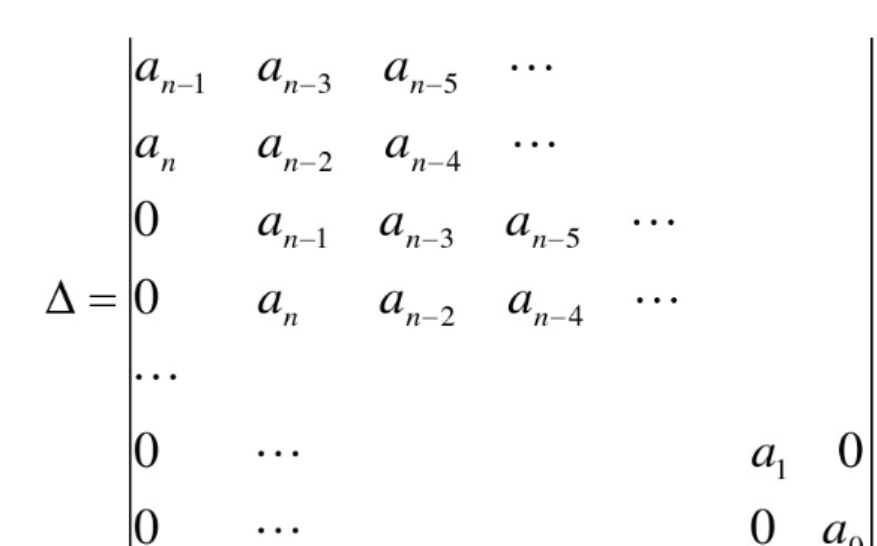
The criterion : Each stage of the principal sub formula is greater than 0
=s+2 Put it into the equation , take u As an equation variable , To solve the .
2.4 Hurwitz The criterion
[ Outside the chain picture transfer in …(img-JIuo2Ql8-1648098107527)]
The criterion : Each stage of the principal sub formula is greater than 0
边栏推荐
- Aircraft collision detection
- Interceptor拦截器
- MySQL 05 存储过程
- Kinect2 for Unity3D——AvatarDemo学习
- 用函数在Excel中从文本字符串提取数字
- Product recommendation and classified product recommendation
- Ruiji takeout SQL table
- 专项测试之「 性能测试」总结
- Was not registered for synchronization because synchronization is not active[resolved]
- MySQL 06 事务、视图、索引、备份和恢复
猜你喜欢
随机推荐
npm的身份证和依赖
Uploading and downloading of files
MySQL 05 存储过程
I'm stupid. When completable future is used with openfegin, it even reports an error
Filebeat.yml configuration file about the configuration of multiple services
Order timeout cancellation and commodity query by category
USB rechargeable hand warmer chip dltap602sc Jericho
Express get/post/delete... Request
SSM项目使用过滤器实现登录监听
Resource for NS2 beginner
Leetcode brushes questions the next day
Here are all the MySQL interview questions you can't expect (the latest version of 2022)
C static method and non static method
Overview of Baidu map technology, and application development of basic API and webapi
Blog Garden beautification tutorial
Aircraft collision detection
Jmeter接口自动化-如何解决请求头Content-Type冲突问题
Led with fan eye protection learning table lamp touch chip-dlt8s12a
Arrays and objects in JS
MySQL 01 关系型数据库设计