当前位置:网站首页>NowCoderTOP28-34二叉树——持续更新ing
NowCoderTOP28-34二叉树——持续更新ing
2022-07-31 09:41:00 【王嘻嘻-】
TOP28. 二叉树的最大深度
public class Solution {
/** * @param root TreeNode类 * @return int整型 */
public int maxDepth (TreeNode root) {
// 层序遍历计算深度
int count = 0;
if(root == null) return 0;
// 队列
Queue<TreeNode> queue = new LinkedList<TreeNode>();
queue.offer(root);
while(!queue.isEmpty()) {
int size = queue.size();
for(int i = 0; i < size ; i++){
TreeNode node = queue.poll();
if(node.left != null) queue.add(node.left);
if(node.right != null) queue.add(node.right);
}
count++;
}
return count;
// // 递归法
// if(root == null) return 0;
// return Math.max(maxDepth(root.left), maxDepth(root.right)) + 1;
}
}
TOP29. 二叉树中和为某一值的路径(一)

public class Solution {
/** * @param root TreeNode类 * @param sum int整型 * @return bool布尔型 */
public boolean hasPathSum (TreeNode root, int sum) {
// 层序遍历
if(root == null) return false;
Queue<TreeNode> queue = new LinkedList<>();
queue.offer(root);
while(!queue.isEmpty()) {
TreeNode node = queue.poll();
if(node.left == null && node.right == null && node.val == sum) {
return true;
}
if(node.left != null) {
node.left.val = node.val + node.left.val;
queue.offer(node.left);
}
if(node.right != null) {
node.right.val = node.val + node.right.val;
queue.offer(node.right);
}
}
return false;
}
// // 前序遍历 递归法
// // 边界条件
// if(root == null) return false;
// // 左右节点为空 即为子节点,且值为给定的和 sum 返回true
// if(root.left == null && root.right == null && root.val == sum) {
// return true;
// }
// return hasPathSum(root.left, sum - root.val) || hasPathSum(root.right, sum - root.val);
// }
}
TOP30. 二叉搜索树与双向链表
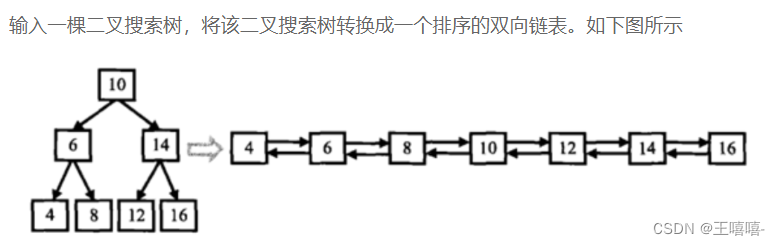
public class Solution {
// 返回的第一个指针即为最小值,先定义为null
public TreeNode head = null;
// 中序遍历当前值的上一位,初始值为最小值,先定为null
public TreeNode pre = null;
public TreeNode Convert(TreeNode pRootOfTree) {
// 中序 叶子为空,则返回
if(pRootOfTree == null) return null;
// 首先递归到最左 最小值
Convert(pRootOfTree.left);
// 找到了 最小值,初始化 head 和 pre
if(pre == null) {
head = pRootOfTree;
pre = pRootOfTree;
}
else{
pre.right = pRootOfTree;
pRootOfTree.left = pre;
pre = pRootOfTree;
}
Convert(pRootOfTree.right);
return head;
}
}
TOP31. 对称的二叉树

public class Solution {
boolean isSymmetrical(TreeNode pRoot) {
// 空树为对称的
if(pRoot == null) return true;
// 辅助队列用于从两边层次遍历
Queue<TreeNode> q1 = new LinkedList<TreeNode>();
Queue<TreeNode> q2 = new LinkedList<TreeNode>();
q1.offer(pRoot.left);
q2.offer(pRoot.right);
while(!q1.isEmpty() && !q2.isEmpty()) {
// 分别从左边和右边弹出节点
TreeNode left = q1.poll();
TreeNode right = q2.poll();
// 都为空 暂时对称
if(left == null && right == null) continue;
// 若有一个不为空,或者元素不等,则不对称
if(left == null || right == null || left.val != right.val) return false;
// 从左往右加入队列
q1.offer(left.left);
q1.offer(left.right);
// 从右向左加入队列
q2.offer(right.right);
q2.offer(right.left);
}
// 都检验完 则为对称
return true;
}
}
TOP32. 合并二叉树

public class Solution {
/** * * @param t1 TreeNode类 * @param t2 TreeNode类 * @return TreeNode类 */
public TreeNode mergeTrees (TreeNode t1, TreeNode t2) {
//若只有一个节点返回另一个,两个都为null自然返回null
if(t1 == null) return t2;
if(t2 == null) return t1;
// 合并根节点
TreeNode head = new TreeNode(t1.val + t2.val);
// 连接后的树的层次遍历节点
Queue<TreeNode> q = new LinkedList<TreeNode>();
// 分别存两棵树的层次遍历节点
Queue<TreeNode> q1 = new LinkedList<TreeNode>();
Queue<TreeNode> q2 = new LinkedList<TreeNode>();
q.offer(head);
q1.offer(t1);
q2.offer(t2);
while(!q1.isEmpty() && !q2.isEmpty()) {
TreeNode node = q.poll();
TreeNode node1 = q1.poll();
TreeNode node2 = q2.poll();
TreeNode left1 = node1.left;
TreeNode left2 = node2.left;
TreeNode right1 = node1.right;
TreeNode right2 = node2.right;
if(left1 != null || left2 != null) {
// 两个节点都存在
if(left1 != null && left2 != null) {
TreeNode left = new TreeNode(left1.val + left2.val);
node.left = left;
// 新节点 入 队列
q.offer(left);
q1.offer(left1);
q2.offer(left2);
}// 只连接一个节点
else if(left1 != null) node.left = left1;
else node.left = left2;
}
if(right1 != null || right2 != null) {
// 两个右节点都存在
if(right1 != null && right2 != null) {
TreeNode right = new TreeNode(right1.val + right2.val);
node.right = right;
// 新节点入队列
q.offer(right);
q1.offer(right1);
q2.offer(right2);
//只连接一个节点
}else if(right1 != null) node.right = right1;
else node.right = right2;
}
}
return head;
}
// // 递归前序遍历
// //若只有一个节点返回另一个,两个都为null自然返回null
// if(t1 == null) return t2;
// if(t2 == null) return t1;
// TreeNode head = new TreeNode(t1.val + t2.val);
// head.left = mergeTrees(t1.left, t2.left);
// head.right = mergeTrees(t1.right, t2.right);
// return head;
// }
}
TOP33. 二叉树的镜像
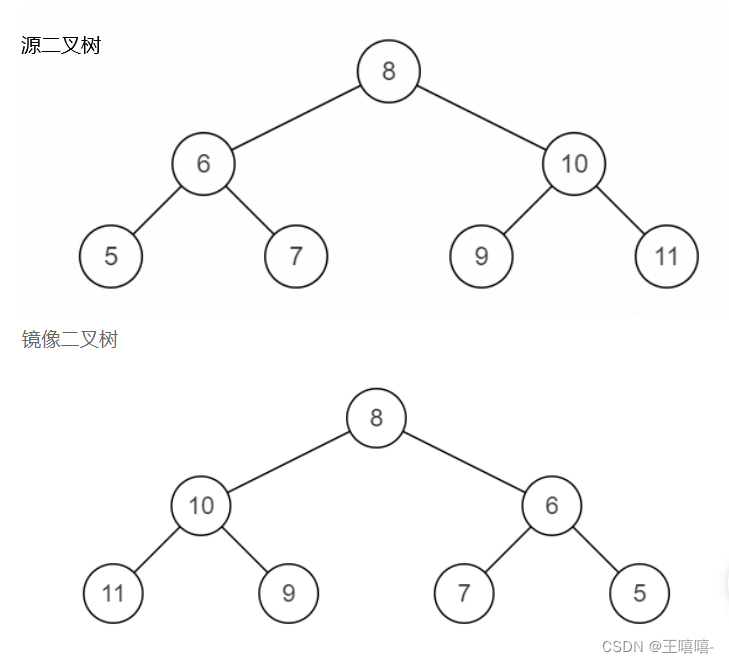
public class Solution {
/** * 代码中的类名、方法名、参数名已经指定,请勿修改,直接返回方法规定的值即可 * @param pRoot TreeNode类 * @return TreeNode类 */
public TreeNode Mirror (TreeNode pRoot) {
// 递归实现
if(pRoot == null) return null;
// 交换
TreeNode temp = pRoot.left;
pRoot.left = pRoot.right;
pRoot.right = temp;
// 递归
pRoot.left = Mirror(pRoot.left);
pRoot.right = Mirror(pRoot.right);
return pRoot;
}
// // 辅助栈
// if(pRoot == null) return null;
// Stack<TreeNode> stack = new Stack<>();
// // 根节点入栈
// stack.add(pRoot);
// while(!stack.isEmpty()) {
// // 节点出栈
// TreeNode node = stack.pop();
// // 根的左右子树入栈
// if(node.left != null) stack.add(node.left);
// if(node.right != null) stack.add(node.right);
// // 左右子树交换
// TreeNode temp = node.left;
// node.left = node.right;
// node.right = temp;
// }
// return pRoot;
// }
}
TOP34. 判断是不是二叉搜索树
public class Solution {
/** * 代码中的类名、方法名、参数名已经指定,请勿修改,直接返回方法规定的值即可 * @param root TreeNode类 * @return bool布尔型 */
// int pre = Integer.MIN_VALUE;
public boolean isValidBST (TreeNode root) {
// 先设置栈用于遍历
Stack<TreeNode> stack = new Stack<TreeNode>();
TreeNode head = root;
// 记录中序遍历的数组
ArrayList<Integer> list = new ArrayList<Integer>();
while(head != null || !stack.isEmpty()) {
// 将左节点入栈,用来保存父问题,直到没有左节点
while(head != null) {
stack.push(head);
head = head.left;
}
head = stack.pop();
// 访问节点
list.add(head.val);
// 进入右边
head = head.right;
}
// 此时访问中序遍历的结果
for(int i = 0; i < list.size() - 1; i++) {
if(list.get(i) > list.get(i + 1)) return false;
}
return true;
}
// 中序遍历
// if(root == null) return true;
// // 左子树
// if(!isValidBST(root.left)) return false;
// if(root.val < pre) return false;
// // 更新最值
// pre = root.val;
// // 再进入右子树
// return isValidBST(root.right);
// }
}
边栏推荐
猜你喜欢
随机推荐
What is the encoding that starts with &#x?
自定义v-drag指令(横向拖拽滚动)
开放麒麟 openKylin 自动化开发者平台正式发布
The fifth chapter
生成随机数
Kotlin—基本语法(二)
Mysql+Navicat for Mysql
Linux 创建mysql数据库并创建账号密码
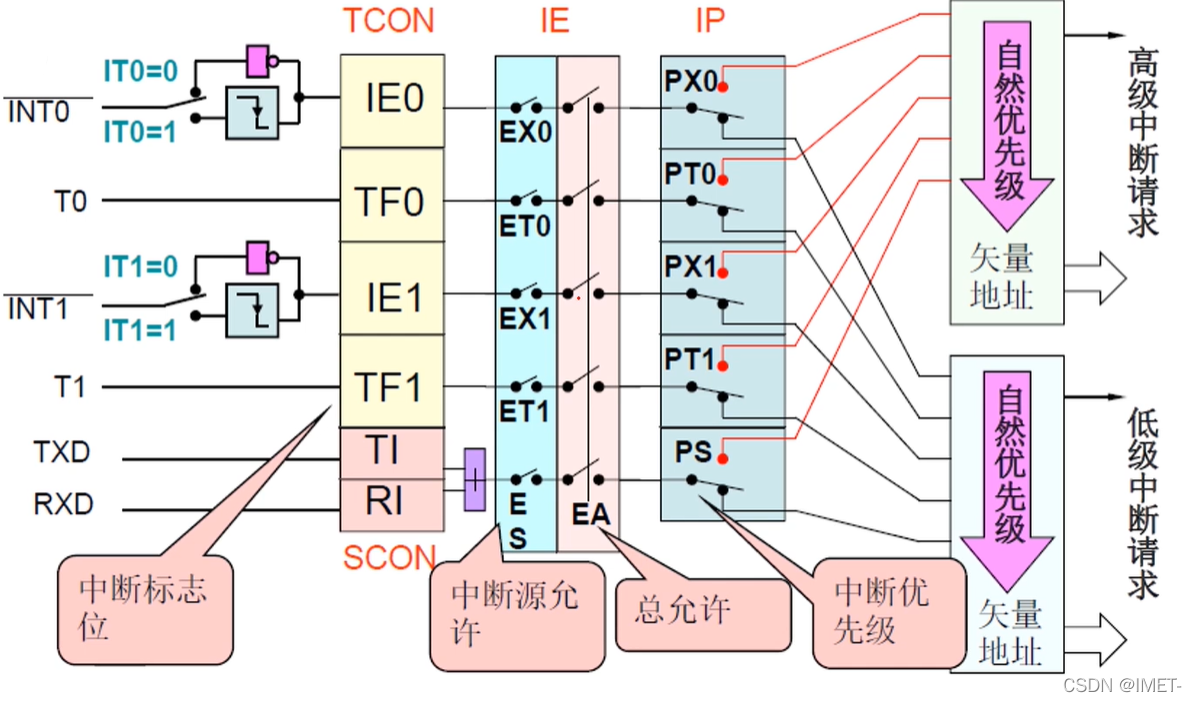
51单片机-----外部中断
JSP session的生命周期简介说明
来n遍剑指--09. 用两个栈实现队列
djangoWeb应用框架+MySQL数据4
Data Middle Office Construction (6): Data System Construction
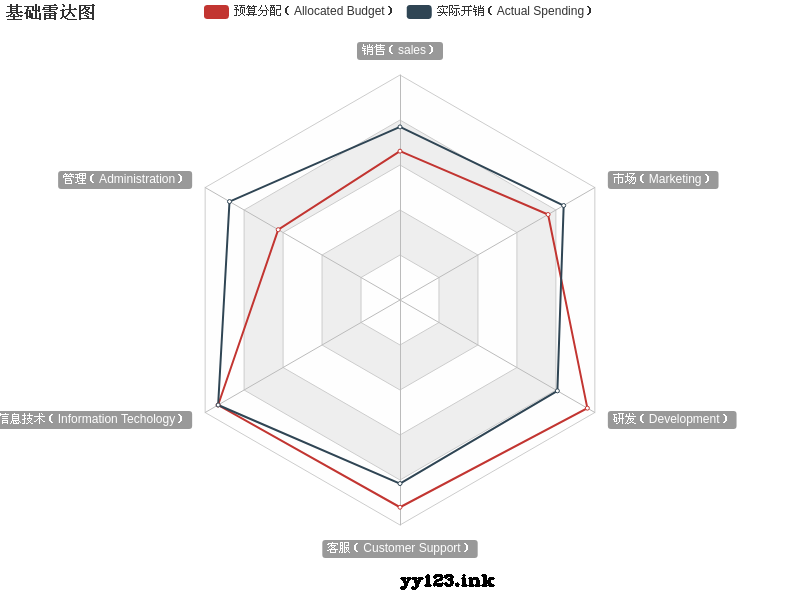
js空气质量aqi雷达图分析
Implement a thread pool
第八章 、接口
postgresql generate random date, random time
A Spark SQL online problem troubleshooting and positioning
(selenium)Service geckodriver unexpectedly exited. Status code was: 64
JSP application对象简介说明