Ten thousand words summarize and realize the commonly used sorting and performance comparison

• The concept of sequencing
• Implementation of common sorting algorithms
  • Bubble sort
  • Selection sort
  • Insertion sort
  • Shell Sort
  • Heap sort
  • Three methods of quick sorting recursive version and non recursive version
    • hoare Law
    • Excavation method
    • Front and back pointer method
    • A non recursive version of the fast queue
  • Recursive and non recursive versions of merge sort
    • Merge sort
    • Non recursive version of merge sort
• Performance comparison of various sorts

---

The concept of sequencing
Sort ： So called sorting , Is to make a series of records or data , According to the size of one or some of the keywords , An operation arranged in ascending or descending order .
stability ： Assume in the sequence of records to be sorted , There are multiple records with the same keyword , Sorted , The relative order of these records remains the same , In the original sequence ,r[i]=r[j], And r[i] stay r[j] Before , In the sorted sequence ,r[i] Still in r[j] Before , We call this sort algorithm stable ; Otherwise it is called unstable .

Implementation of common sorting algorithms

// Exchange data 
void Swap(int* p1, int* p2)
{
    
	int tmp = *p1;
	*p1 = *p2;
	*p2 = tmp;
}
//  Bubble sort 
void BubbleSort(int* a, int n)
//  Selection sort 
void SelectSort(int* a, int n);
//  Insertion sort 
void InsertSort(int* a, int n);
//  Shell Sort 
void ShellSort(int* a, int n);
//  Heap sort 
void AdjustDwon(int* a, int n, int root);
void HeapSort(int* a, int n);

//  Quick sort recursive implementation 
//  Quick sort hoare edition 
int PartSort1(int* a, int left, int right);
//  Quick sort digging 
int PartSort2(int* a, int left, int right);
//  Pointer before and after quick sort 
int PartSort3(int* a, int left, int right);
void QuickSort(int* a, int left, int right);

//  Quick sort   Non recursive implementation 
void QuickSortNonR(int* a, int left, int right)

//  Merge sort recursive implementation 
void MergeSort(int* a, int n)
//  Merge sort non recursive implementation 
void MergeSortNonR(int* a, int n)

Bubble sort
Time complexity ：O($N^2$)
Spatial complexity ：O(1)
stability ： Stable
thought ： Traverse through double-layer loops , Compare two adjacent numbers at a time , If it's in ascending order （a[j]>a[j+1]）, Exchange it for , Bubble the maximum value each time through the cycle , Next time is the next big value , Finally, the order of data is achieved .

void BubbleSort(int* a, int n)
{
    
	assert(a);

	for (int i = 0; i < n; i++)
	{
    
		int flag = 0; // If the data is in ascending order   You can achieve O（N）
		for (int j = 1; i < n - j; j++)
		{
    
			if (a[j - 1] > a[j])
			{
    
				Swap(&a[j - 1], &a[j]);// Functions that exchange data Swap
				flag = 1;
			}
		}
		if (flag == 0)
		{
    
			break;
		}
	}

Selection sort
Time complexity ：O($N^2$)
Spatial complexity ：O(1)
stability ： unstable
thought ：
1. Select the maximum value in the data by looping max Minimum value min.
2. Put the maximum value max Place the last data , minimum value min Put it at the beginning , If the data is not in the corresponding position , Exchange with the location of these two data .
3. In the balance （array[i+1]–array[n-1]） Collection , Repeat the above steps , Until the set remains 1 Elements or 0 Elements , Odd number remaining 1 individual , Even number remaining 0 individual .

void SelectSort(int* a, int n)
{
    
	assert(a);

	int begin = 0;
	int end = n - 1;
	while (begin < end)                 
	{
    
		int mini = begin; // Used to store minimum value 
		int maxi = begin; // Used to store the maximum 
		for (int i = begin + 1; i <= end; i++)
		{
    
			if (a[i] < a[mini])// If i The value of is smaller than the minimum   Just change the minimum value 
			{
    
				mini = i;
			}
			if (a[i] > a[maxi])// If i The value of is larger than the maximum   Change the maximum value 
			{
    
				maxi = i;
			}
		}
		Swap(&a[begin], &a[mini]);
		// If begin The location and maxi The positions of overlap , Namely maxi stay begin The location of  
		// and begin It happened to be mini The exchange went away 
		// It needs to be corrected maxi The location of   After the exchange mini;
		if (begin == maxi)
		{
    
			maxi = mini;
		}
		Swap(&a[end], &a[maxi]); // Functions that exchange data Swap
		begin++;
		end--;
	}
}

Insertion sort
Time complexity ：O($N^2$)
Spatial complexity ：O(1)
stability ： Stable
thought ： In an orderly interval , Insert the data into its corresponding position . You can put array[i] The position of is regarded as an ordered interval ,array[i+1] If the location of is larger than it, there is no need to move the data , Smaller than it array[i+1] Insert into i Location , then array[i] This data moves back , Cycle this step , Until the data in the set is in order .
The following uses the dynamic graph found on the Internet to show the process of insertion sorting

void InsertSort(int* a, int n)
{
    
	assert(a);
	for (int i = 0; i < n - 1; i++)
	{
    
		int end = i;
		int tmp = a[end + 1];
		while (end >= 0)
		{
    
			if (tmp < a[end])      // Ascending  ： If +1 If the number of positions is less than the previous number, move the data  
			{
    
				a[end + 1] = a[end];
				end--;
			}
			else
			{
    
				break;
			}
		}
		a[end + 1] = tmp;
	}
}

Shell Sort
Time complexity ：O($N^{1.3}$) about Hill's complexity calculation is very difficult , In about 1.3 about , Didn't arrive 2 times
stability ： unstable
thought ： Hill sort is an optimization of insert sort .
1. Choose an integer first , Divide all records in the set to be sorted into K A set of , All distances are N The records are grouped in the same group , And sort the records in each group .
2. then , Repeat the above work of grouping and sorting and reduce the distance until N=1.
3. stay N>1 All the things you do are called the pre sort of Hill sort , The purpose is to make the set more orderly , When N=1 when , All records will be arranged in a group .

void ShellSort(int* a, int n)
{
    
	assert(a);
	int gap = n;
	while (gap > 1)
	{
                         // use gap As the initial distance , Every time you let gap/3 Zoom out 
		gap = gap / 3 + 1;// leave ,+1 For the last time gap It must be 1, Form an orderly 
		for (int i = 0; i < n - gap; i++)
		{
    
			int end = i;
			int tmp = a[end + gap];
			while (end >= 0)
			{
    
				if (tmp < a[end])
				{
    
					a[end + gap] = a[end];
					end -= gap;
				}
				else
				{
    
					break;
				}
			}
			a[end + gap] = tmp;
		}
	}
}

Heap sort
Time complexity ：O($N\ast log{2}^N$)
Spatial complexity ：O(1)
stability ： unstable
thought ： Here we need to sort with the help of the characteristics of the heap .
1. Use downward adjustment , Build the data into a pile , Be careful ： In ascending order, a lot of , Descending heap
2. Adjust by cycling , After each adjustment , The data at the top of the heap is the maximum , Then exchange with the last data in the heap , Put the maximum value at the end .
3. Every time you exchange data, you need to adjust the heap , Don't treat the last value as data in the heap , Adjustment , Pick out the next largest value , Repeat this step , Until the last value .

// Downward adjustments 
void AdjustDwon(int* a, int size, int parent)
{
    
	int child = parent * 2 + 1;
	while (child < size)
	{
                                 // In ascending order   Descending heap 
		if (child + 1 < size && a[child + 1] > a[child])
		{
    
			child++;
		}
		if (a[child] > a[parent])
		{
    
			Swap(&a[child], &a[parent]);
			parent = child;
			child = parent * 2 + 1;
		}
		else
		{
    
			break;
		}
	}
}
void HeapSort(int* a, int n)
{
    
	assert(a);   //i Adjust from the penultimate non leaf node , Leaf nodes need not be adjusted 
	for (int i = (n - 1 - 1) / 2; i >= 0; i--) 
	{
    
		AdjustDwon(a, n, i);
	}
	int flag = n - 1; // Start from the last leaf node 
	while (flag > 0)
	{
    
		Swap(&a[0], &a[flag]); // The maximum and minimum values at the top of the heap are exchanged 
		AdjustDwon(a, flag, 0);// When adjusting, ignore the last value of the heap after exchange  
		                       // Don't treat it as data in the heap   The end of adjustment is ascending 
		flag--;
	}
}

Three methods of quick sorting recursive version and non recursive version
Time complexity ：O($N\ast log{2}^N$)
Spatial complexity ：O($log{2}^N$)
stability ： unstable
thought ： Take any element in the element sequence to be sorted as the benchmark , According to the benchmark value, the set to be sorted is divided into left and right subsequences , All elements in the left subsequence are less than the base value , All elements in the right subsequence are greater than the base value , Then the leftmost and rightmost subsequences repeat the process , Until all the elements are aligned in their respective positions .

// Take the three Numbers   This is a subfunction that must be used for fast scheduling , Used to choose key As a reference value 
int GetMidIndex(int* a, int begin, int end);
{
    
	assert(a);
	int mid = (begin + end) / 2; // Take the value in the middle of the data as mid

	if (a[begin] < a[mid])
	{
    
		if (a[mid] < a[end])   // If begin < mid < end  The median is :mid
		{
    
			return mid;
		}
		else if (a[end] < a[begin])// If end < begin < mid The median is :begin
		{
    
			return begin;
		}
		else
		{
    
			return end;    // If begin < mid  also mid > end also end > begin  The median is :end
		}
	}
	else 	                         //a[begin] > a[mid]
	{
    
		if (a[end] < a[mid])         // If begin > mid > end  The median is :mid
		{
    
			return mid;
		}
		else if (a[begin] < a[end]) // If end > begin > mid  The median is :begin
		{
    
			return begin;
		}
		else
		{
    
			return end;             // If begin>mid  also end > mid  also begin > end  The median is :end
		}
	}
}
// Quick sort 
void QuickSort(int* a, int begin, int end);
//Hoare Law 
int PartSort1(int* a, int begin, int end);
// Excavation method 
int PartSort2(int* a, int begin, int end);
// Front and back pointer method 
int PartSort3(int* a, int begin, int end);

hoare Law
thought ：
1. First select the value of any element as key At baseline , Here we realize the middle of three numbers , Suppose we select the value of the first position on the left , Let me define one more left The variable represents the value of the first position , One right The variable represents the value of the last position ,left The goal is to compare key Big elements ,right The goal is to compare key Small elements .
2. Be sure to use triple arithmetic to find the position of the middle value of the array , Then exchange with the value of the first position , If you don't use triple Center , Then if the value of the first position is just a small value , Then the efficiency will be very low .
3. If we choose the value of the first element on the far left as key At baseline , Then you need the right right Go ahead , On the contrary, go first on the left , Find a comparison key Small value , When you find it, stop ,left To walk again , Find a comparison key Big value , etc. left And right When they all stop and the positions are not equal , Just exchange the value of their positions , Then repeat this step , until left And right meet , Stop when you meet , In exchange for key The value of the position and the position where it stops .
4. Finally, use recursion , Sort by repeatedly narrowing the range , such as 0~10 Section , For example, sort first 0-5 Section ,0-5 This interval is divided into 0-2 and 3-5 Two intervals , Until it can no longer be divided , If 0-2 and 3-5 After the interval is ordered , that 0-5 The intervals are ordered , Reordering 6-10 Section , etc. 6-10 After the interval is ordered , Then the whole will be orderly .
The following is a moving picture display found on the Internet hoare The process of law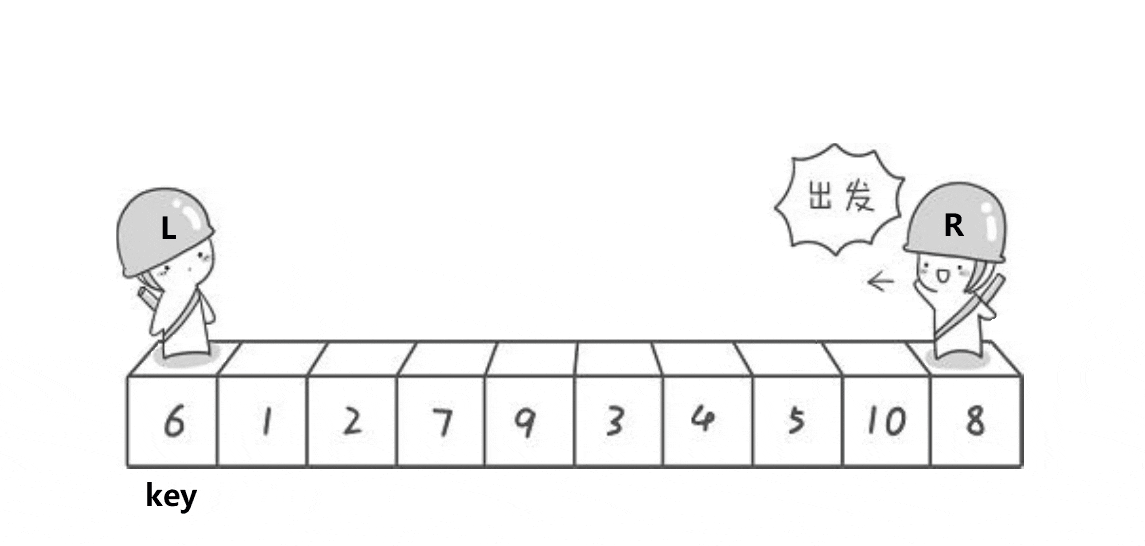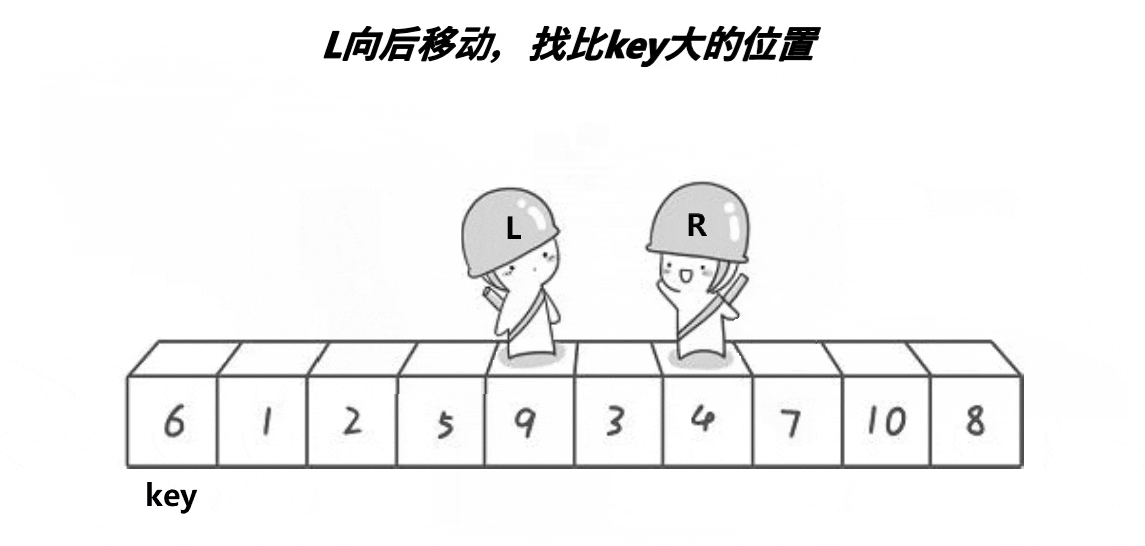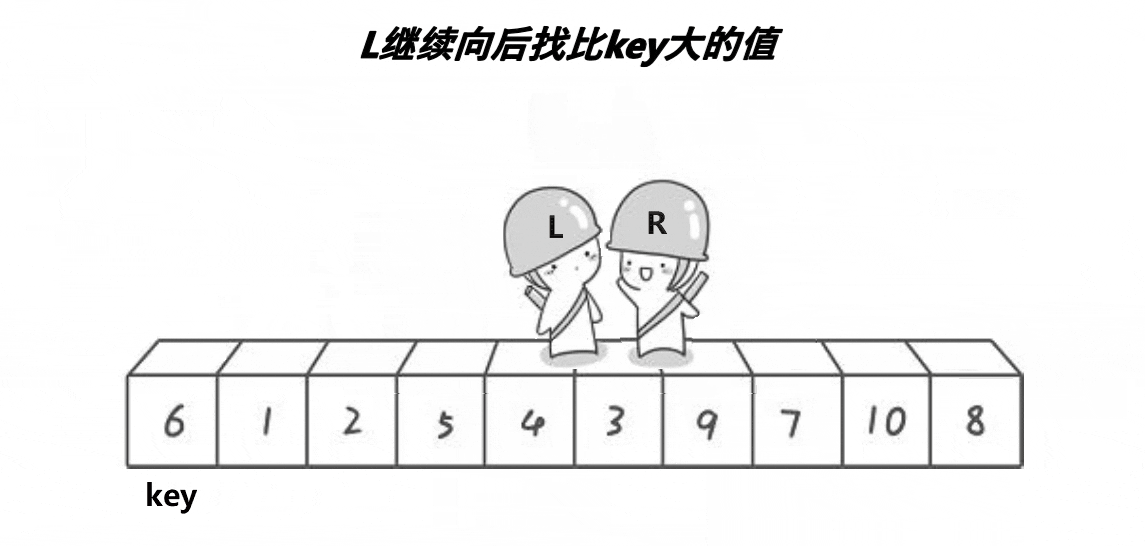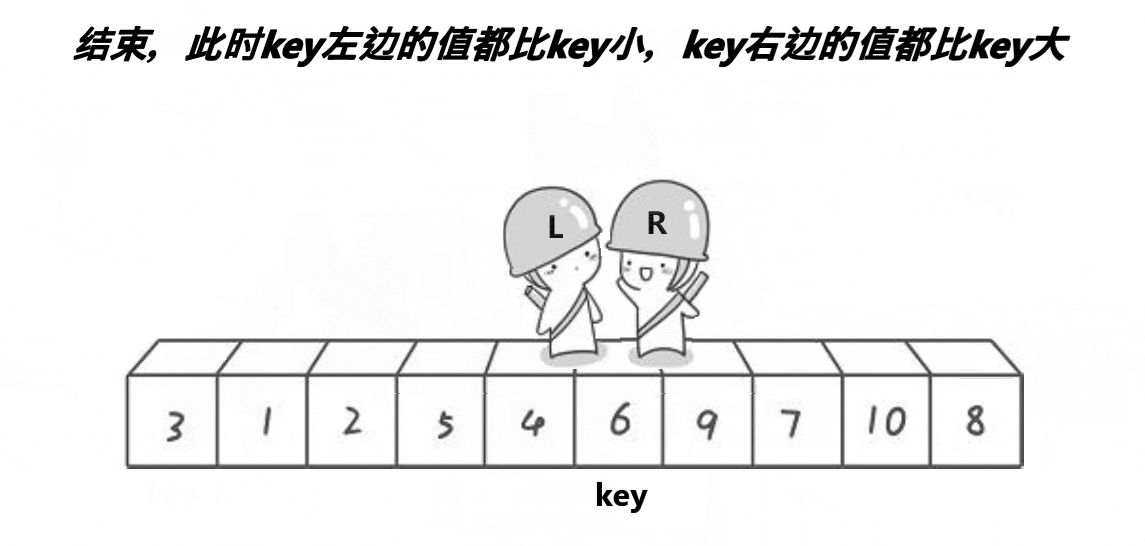

int PartSort1(int* a, int begin, int end)
{
    
	assert(a);
	int left = begin;
	int right = end;
	int keyi = left;// Choose the left to do keyi It's the reference value   Choose the left to do keyi  Just go first on the right 
                    // Choose the right side to do keyi, Go first on the left 
	int midi = GetMidIndex(a, begin, end);    
	Swap(&a[keyi], &a[midi]);           

	while (left < right)
	{
    
		// Go first on the right , Find a comparison keyi Small value , If left and right Stop when you meet 
		while (left < right && a[right] >= a[keyi])
		{
    
			right--;
		}
		// Go left , Find a comparison keyi Big value , If left and right Stop when you meet 
		while (left < right && a[left] <= a[keyi])
		{
    
			left++;
		}

		Swap(&a[left], &a[right]);
	}
	Swap(&a[keyi], &a[left]);  // In exchange for keyi and left And right Where we met   The meeting place must be better than keyi smaller 
	keyi = left;

	return keyi;
}
void QuickSort(int* a, int begin, int end)
{
                 // This method is similar to the preorder traversal of binary trees ,
	assert(a);
	if (begin >= end)
	{
    
		return;
	}
	int keyi = PartSort1(a, begin, end);
	QuickSort(a, begin, keyi - 1);// Recursive left half interval 
	QuickSort(a, keyi + 1, end);// Then recurse the right half interval 
}

Excavation method
thought ：
1. Compared with hoare Law , The digging method has not changed much , Suppose we choose the value of the first element on the left as key At baseline , Let me define one more left The variable represents the value of the first position , One right The variable represents the value of the last position ,left The goal is to compare key Big elements ,right The goal is to compare key Small elements .
2. Be sure to use triple arithmetic to find the position of the middle value of the array , Then exchange with the value of the first position , If you don't use triple Center , Then if the value of the first position is just a small value , Then the efficiency will be very low .
3. First save key The value of the reference value , then right Find a comparison first key Small value , Think of the first position as a pit , And then put right Put the stopped value into the pit ,right The position of becomes a pit , then left Look for a comparison key Big value , Find it and put it in the pit ,left The position is the next pit , The last meeting place is put into the first saved key The value of the reference value .
4. Finally, use recursion , Sort by repeatedly narrowing the range , such as 0~10 Section , For example, sort first 0-5 Section ,0-5 This interval is divided into 0-2 and 3-5 Two intervals , Until it can no longer be divided , If 0-2 and 3-5 After the interval is ordered , that 0-5 The intervals are ordered , Reordering 6-10 Section , etc. 6-10 After the interval is ordered , Then the whole will be orderly .
The following uses the dynamic diagram found on the Internet to show the process of excavation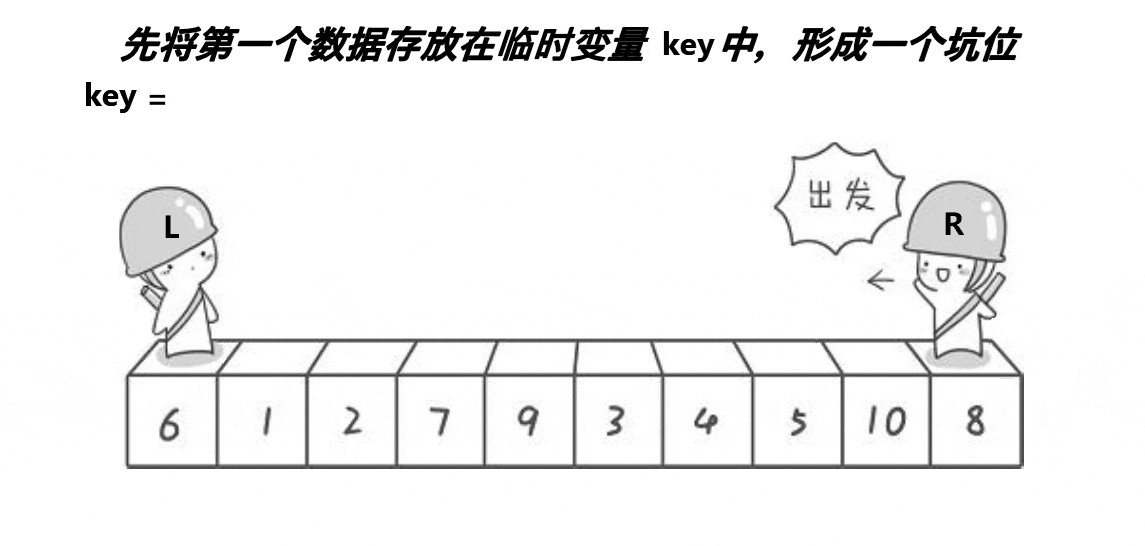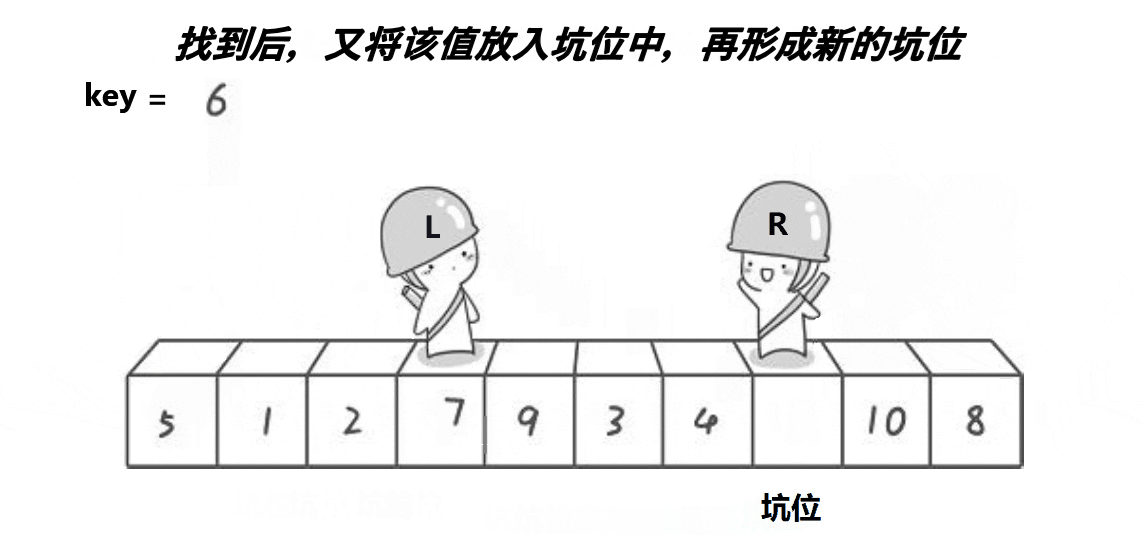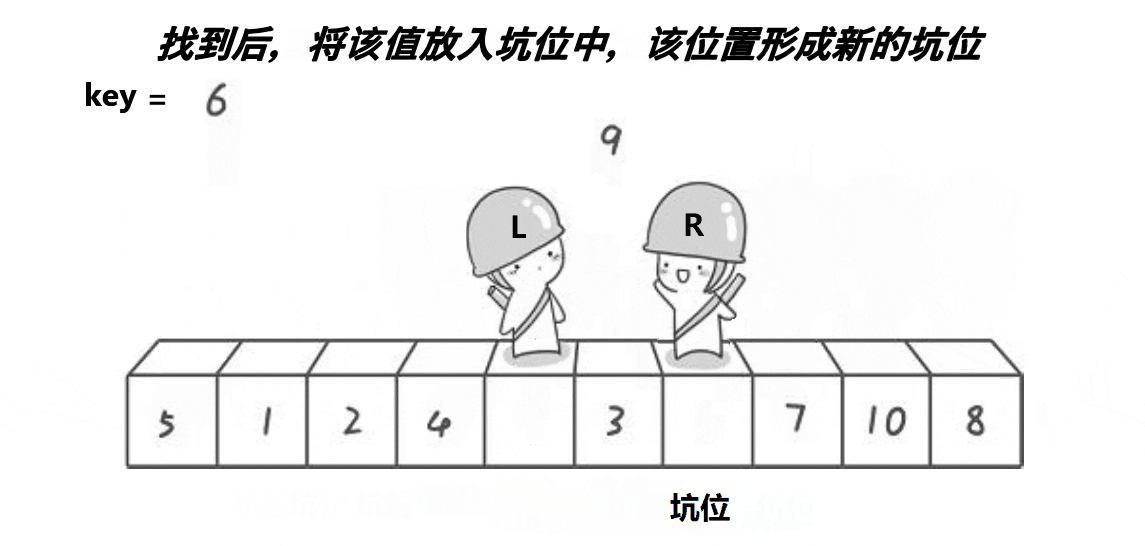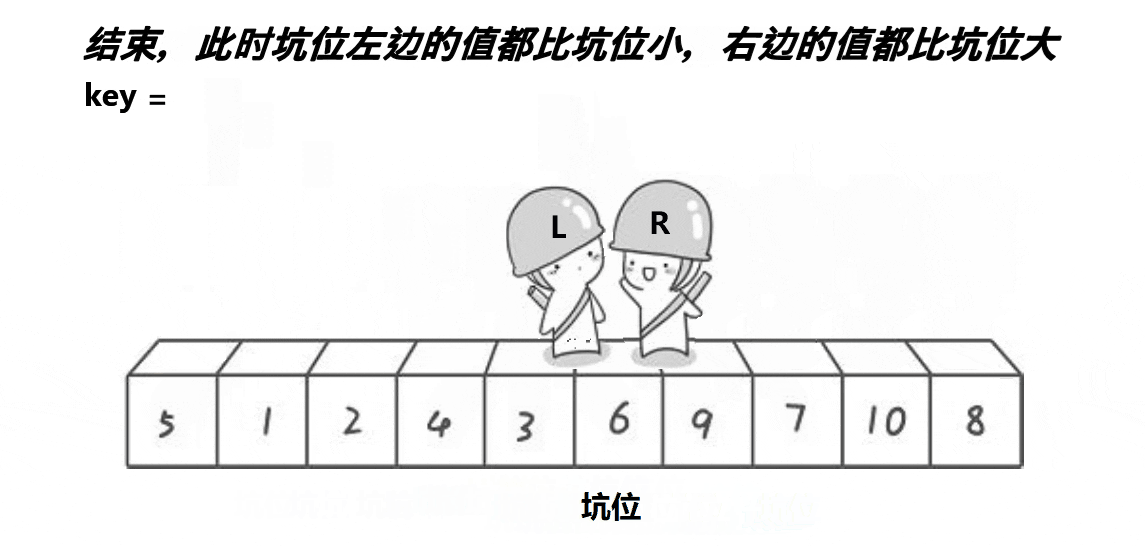

int PartSort2(int* a, int begin, int end)
{
    
	assert(a);
	int keyi = begin;// At baseline 

	int midi = GetMidIndex(a, begin, end);// Take the middle value of three numbers as keyi  At baseline 
	Swap(&a[keyi], &a[midi]);             // Swap the middle value with the leftmost value   The left side is still the reference value   The idea of going first on the right 
	int flag = a[begin];                  // use flag To save the benchmark   Prevent pit digging   Subsequently, the reference value is overwritten  

	int piti = begin;// pit 
	while (begin < end)
	{
    
		while (begin < end && a[end] >= flag)
		{
    
			end--;
		}
		a[piti] = a[end];// Look for a small on the right   Then put it into the pit 
		piti = end;// Update the pit to end The location of 
		while (begin < end && a[begin] <= flag)
		{
    
			begin++;
		}
		a[piti] = a[begin];// Look big on the left   Then put it into the pit 
		piti = begin;// Update the pit to begin The location of 
	}
	a[piti] = flag; // The value of the last pit is   At baseline   The left ratio of the reference value keyi Small , On the right and vice versa 

	return piti; // Returns the position of the reference value 
}
void QuickSort(int* a, int begin, int end)
{
    
	assert(a);
	if (begin >= end)
	{
    
		return;
	}
	int keyi = PartSort2(a, begin, end);
	QuickSort(a, begin, keyi - 1);
	QuickSort(a, keyi + 1, end);
}

Front and back pointer method
thought ：
1. Use the intermediate value found in the three numbers to serve as the reference value , That is to say key, Create two more pointers prev and cur,cur Traverse the contents of the array before ,prev rearwards , If cur Meet than key Smaller value , that prev++ Just take a step backwards , If you meet Bi key Big value , that prev The pointer doesn't move ,cur The pointer continues , Until the next ratio key Small values appear , At this time, put cur The value of the location prev++ The value of the position is exchanged , Repeat this step , wait until cur Go to the NULL when ,prev The location and key The value of .
2. Finally, use recursion , Sort by repeatedly narrowing the range , such as 0~10 Section , For example, sort first 0-5 Section ,0-5 This interval is divided into 0-2 and 3-5 Two intervals , Until it can no longer be divided , If 0-2 and 3-5 After the interval is ordered , that 0-5 The intervals are ordered , Reordering 6-10 Section , etc. 6-10 After the interval is ordered , Then the whole will be orderly .
The following uses the dynamic diagram found on the Internet to show the process of the front and back pointer method

int PartSort3(int* a, int begin, int end)
{
    
	assert(a);
	int prev = begin;
	int cur = begin + 1;
	int keyi = begin;

	int midi = GetMidIndex(a, begin, end);  // Take the middle value of three numbers as keyi  At baseline 
	Swap(&a[keyi], &a[midi]);               // Swap the middle value with the leftmost value   Still, the leftmost is the benchmark   The idea of going first on the right 

	while (cur <= end)
	{
    
		if (a[cur] < a[keyi] && prev++ != cur) // Be careful : prev Only in cur Less than keyi It's only when I'm in the mood ++
		{
    
			Swap(&a[prev], &a[cur]);
		}

		cur++;          // After encountering a value larger than the reference value  cur++ prev Immobility , Until you meet the next number smaller than the benchmark 
	}
	Swap(&a[prev], &a[keyi]);// Exchange the reference value to the end of the cycle   Make the left and right sides of the benchmark orderly ;
	keyi = prev;

	return keyi; // Returns the position of the reference value 
}
void QuickSort(int* a, int begin, int end)
{
    
	assert(a);
	if (begin >= end)
	{
    
		return;
	}
	int keyi = PartSort3(a, begin, end);
	QuickSort(a, begin, keyi - 1);
	QuickSort(a, keyi + 1, end);
}

A non recursive version of the fast queue
thought ： Here you need to use the stack to complete non recursive , Take advantage of the last in, first out feature of the stack , First press the interval to be sorted into the stack , The assumption is 0-10 This interval is sorted , Enter first 10 Enter again 0, Then use the front and back pointer method , Determine a reference value key, After ordering key It must be in its right position , hypothesis key yes 5, Then the interval is divided into ,0-4 and 6-10, Then enter the right half of the stack , Re enter the left half , Because the stack is last in first out , So we need to enter the second half first , Keep cycling this step , Until the right half of the interval has been ordered , Then row the left half , Finally, there is no interval in the stack that needs to be sorted , The array is sorted .

void QuickSortNonR(int* a, int begin, int end)
{
    
	assert(a);
	ST st;
	StackInit(&st);
	StackPush(&st, end);  // The first end Pressing stack 
	StackPush(&st, begin); // Recompression begin

	while (!StackEmpty(&st))  // Wait until there are no elements in the stack   The array is ordered 
	{
    
		int left = StackTop(&st);//left It's equal to the one pressed in later begin
		StackPop(&st);

		int right = StackTop(&st); //right It's equal to pressing the stack first end
		StackPop(&st);

		int keyi = PartSort3(a, left, right); // After a single sequence  keyi The left and right sides of the are orderly 
		//a[left]-a[keyi-1] keyi a[keyi+1]-a[right] // At this time, we only need to arrange these two intervals in order   The whole thing is in order 

		if (keyi + 1 < right) // If keyi The interval on the right is greater than 1 Or if the interval does not exist, there is no need to press the stack  
		{
    
			StackPush(&st, right);
			StackPush(&st, keyi + 1);
		}
		if (left < keyi - 1)  // Ditto on the left   After pressing the stack, determine after sorting keyi  Continue sorting after being divided into subintervals   Until interval <=1 until 
		{
    
			StackPush(&st, keyi - 1);
			StackPush(&st, left);
		}
	}

	StackDestroy(&st);
}

Recursive and non recursive versions of merge sort
Time complexity ：O($N\ast log{2}^N$)
Spatial complexity ：O(N)
stability ： Stable

// Merge sort 
void MergeSort(int* a, int n);
// Merge sort subfunction 
void _MergeSort(int* a, int begin, int end, int* tmp);
// Merge sort non recursive version 
void MergeSortNonR(int* a, int n);

Merge sort
thought ：
1. First divide the array into two intervals , These two intervals are divided again by recursion , Until it is divided into an indivisible , Then compare the size and exchange the location of the data , And then merge , In this process, we need to save the data sequence after comparison with the help of additional arrays , Finally, copy back to the original array , Wait until the left half of the interval is in order , Then recurse the right half interval to sort , After the left and right ranges are merged , Carry out a merger as a whole , And sort , Finally, the overall order is achieved .
2. This process is the same as the idea of post order traversal in binary tree , First recurse the left half interval , Then recurse the right half interval , Finally, the overall merger will form an orderly .
The following uses the dynamic graph found on the Internet to show the process of merging and sorting

// Merge sort subfunction 
void _MergeSort(int* a, int begin, int end, int* tmp)
{
    
	assert(a);
	if (begin >= end) // If the interval does not exist or there is only one value left in the interval   I think this interval is ordered 
	{
    
		return;
	}
	int mid = (begin + end) / 2; 
	// Divide this interval into left and right intervals 
	//a[begin]-a[mid] a[mid+1]-a[end]

	_MergeSort(a, begin, mid, tmp); // Recurse these two intervals in a postorder way 
	_MergeSort(a, mid + 1, end, tmp);
	
	// Merge data 
	int begin1 = begin, end1 = mid;
	int begin2 = mid + 1, end2 = end;
	int i = begin;                            //i Cannot from 0 Start   Want to be with begin1 In the same position   The merged data should correspond to the position of the original array 
	while (begin1 <= end1 && begin2 <= end2)  // Comparative data   Put the small ones in i Corresponding position  
	{
    
		if (a[begin1] < a[begin2])
		{
    
			tmp[i++] = a[begin1++];
		}
		else
		{
    
			tmp[i++] = a[begin2++];
		}
	}
	while (begin1 <= end1) // The upper cycle ends   There must be an array whose data is not completely put in tmp In array   Put the remaining data into tmp Array 
	{
    
		tmp[i++] = a[begin1++];
	}
	while (begin2 <= end2) // These two cycles will only enter one   Don't distinguish  
	{
    
		tmp[i++] = a[begin2++];
	}

	// Copy the merged data back to the original array 
	memcpy((a + begin), (tmp + begin), (end - begin + 1)*sizeof(int));
}
// Merge sort 
void MergeSort(int* a, int n)
{
    
	assert(a);
	int* tmp = (int*)malloc(sizeof(int) * n);// Extra open array 
	assert(tmp);

	_MergeSort(a, 0, n - 1, tmp);
	free(tmp);
}

Non recursive version of merge sort
thought ： Use arrays to merge , First set a distance value gap, Compare and transpose every two elements with different distance values , After comparison , Put in a temporary array , Wait until all the elements in the array are sorted for the first time , Then copy back to the original array , Then the distance value gap With 2 Times the way to grow , Merge one by one from the beginning , Merge in pairs , until gap Not less than n until , In the process of merging, it is possible that the calculated interval will cross the boundary , Remember to modify the boundary , To complete the merging , Finally, the whole is merged , Achieve the order of the array .

void MergeSortNonR(int* a, int n)
{
    
	assert(a);
	int* tmp = (int*)calloc(sizeof(int) * n, sizeof(int));
	assert(tmp);

	int gap = 1;
	while (gap < n)//gap  Represents the distance of each merging   When gap The last time is less than n when   Is the last merge of the total number of arrays 
	{
    
		for (int i = 0; i < n; i += 2 * gap) 
		{
    
			//[i, i + gap - 1] [i + gap, i + 2 * gap - 1] 
			int begin1 = i, end1 = i + gap - 1;
			int begin2 = i + gap, end2 = i + 2 * gap - 1;

			// Correct the boundary crossing 
			if (end1 >= n)
			{
    
				end1 = n - 1; 

				begin2 = n;  
				end2 = n - 1;
			}
			else if (begin2 >= n)
			{
    
				begin2 = n; 
				end2 = n - 1;
			}
			else if (end2 >= n) 
			{
    
				end2 = n - 1;
			}
			
			// Merge data 
			int j = begin1;                            //i Cannot from 0 Start   Want to be with begin1 In the same position   The merged data should correspond to the position of the original array 
			while (begin1 <= end1 && begin2 <= end2)   // Comparative data   Put the small ones in i Corresponding position  
			{
    
				if (a[begin1] < a[begin2])
				{
    
					tmp[j++] = a[begin1++];
				}
				else
				{
    
					tmp[j++] = a[begin2++];
				}
			}
			while (begin1 <= end1) // The upper cycle ends   There must be an array whose data is not completely put in tmp In array   Put the remaining data into tmp Array 
			{
    
				tmp[j++] = a[begin1++];
			}
			while (begin2 <= end2) // These two cycles will only enter one   Don't distinguish  
			{
    
				tmp[j++] = a[begin2++];
			}
		}
		// Copy the merged data back to the original array 
		memcpy(a, tmp, sizeof(int) * n);
		gap *= 2; //gap With 2 To the power of   To merge two by two 
	}
	free(tmp);
}

Performance comparison of various sorts
summary ： From the results of the console operation below, we can see the performance gap of the commonly used sorting , If you sort by 100000 arrays in the following array ,O($N\ast log{2}^N$) Our sorting algorithm only needs less than 1 You can arrange the array in seconds , and O($N^2$) The sorting algorithm of needs to be close to 5 Seconds to complete , As for bubble sorting, it also took a whole 43 It takes only seconds to sort 100000 data , You can see it here O($N\ast log{2}^N$) The sorting algorithm of and O($N^2$) The difference of sorting algorithm is too obvious .

// Performance test of various sorts 
void TestOP()
{
    
    // establish 7 An array , Put 100000 data to sort and compare 
	srand(time(0));
	const int N = 100000;
	int* a1 = (int*)malloc(sizeof(int) * N);
	int* a2 = (int*)malloc(sizeof(int) * N);
	int* a3 = (int*)malloc(sizeof(int) * N);
	int* a4 = (int*)malloc(sizeof(int) * N);
	int* a5 = (int*)malloc(sizeof(int) * N);
	int* a6 = (int*)malloc(sizeof(int) * N);
	int* a7 = (int*)malloc(sizeof(int) * N);

	for (int i = 0; i < N; ++i)
	{
    
		a1[i] = rand();
		a2[i] = a1[i];
		a3[i] = a1[i];
		a4[i] = a1[i];
		a5[i] = a1[i];
		a6[i] = a1[i];
		a7[i] = a1[i];
	}
	int begin1 = clock();
	InsertSort(a1, N);
	int end1 = clock();

	int begin2 = clock();
	ShellSort(a2, N);
	int end2 = clock();

	int begin3 = clock();
	SelectSort(a3, N);
	int end3 = clock();

	int begin4 = clock();
	HeapSort(a4, N);
	int end4 = clock();

	int begin5 = clock();
	QuickSort(a5, 0, N - 1);
	int end5 = clock();

	int begin6 = clock();
	MergeSort(a6, N);
	int end6 = clock();

	int begin7 = clock();
	BubbleSort(a7, N);
	int end7 = clock();

	printf(" Insertion sort ：InsertSort:%d\n", end1 - begin1);
	printf(" Shell Sort ：ShellSort:%d\n", end2 - begin2);
	printf(" Selection sort ：SelectSort:%d\n", end3 - begin3);
	printf(" Heap sort  ：HeapSort:%d\n", end4 - begin4);
	printf(" Quick sort ：QuickSort:%d\n", end5 - begin5);
	printf(" Merge sort ：MergeSort:%d\n", end6 - begin6);
	printf(" Bubble sort ：BubbleSort:%d\n", end7 - begin7);

	free(a1);
	free(a2);
	free(a3);
	free(a4);
	free(a5);
	free(a6);
	free(a7);
}
int main()
{
    
	TestOP();
	return 0;
}