[fundamentals of machine learning 02] decision tree and random forest

Decision tree

The figure above is the legend of a decision tree , Then the mathematical expression of the decision tree is ：
$$G(\mathbf{x})=\sum _{t=1}^T{q}_t(\mathbf{x})\cdot g_t(\mathbf{x})$$
among $g_t(\mathbf{x})$ It is also a decision tree ,$q(x)$ It means $x$ Whether in $G$ The path of $t$ in . From the perspective of recursive tree ：

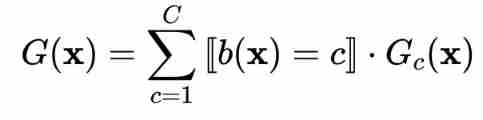
among ：

• $G(x)$ : full-tree hypothesis（ The full tree model of the current root node ）
• $b(x)$ : branching criteria（ Determine which branch ）
• $G_c(x)$: sub-tree hypothesis at the c-th branch（ The first c Subtree of branches ）

Then the training process of decision tree is ：

From the intuitive training process , We can see that there are four problems that need to be confirmed ：

• number of branches（ Number of branches ）$C$
• branching criteria（ Branch condition ）$b(\mathbf{x})$
• termination criteria（ Termination conditions ）
• base hypothesis（ Base assumption function ）$ g_t( \mathbf { x } )$

With so many options , There are many ways to implement the decision tree model , A common decision tree CART Trees （Classification and Regression Tree（C&RT））

C&RT

So how to solve the above four problems ：

1. Use a binary tree . The number of branches is 2（ Binary tree ）, Use decision stump（ namely $ b( \mathbf { x })$ Implementation method ） Go into segments .
2. Branch condition $b(\mathbf{x})$ That is, how to branch , Best branching function （ Model ） Selection of , Two parts of data used Yes No “ pure ” , First judge the purity of each segment of data, and then calculate the average value , As this decision stump Whether the evaluation criteria are selected .

$$b(\mathbf{x})=\underset{\text{ decision stumps }h(\mathbf{x})}{\mathrm{argmin}}\sum _{c=1}^2\mid {\mathcal{D}}_c\text{ with }h\mid \cdot \text{ impurity }\left({\mathcal{D}}_c\text{ with }h\right)$$

3. Base assumption function $g_t$ Is constant .
4. The termination condition is that it cannot be in the branch （ All of the $y_n$ or ${\mathbf{x}}_n$ Are all the same , That is, stop when the impurity is zero or the decision can no longer be made ）.

C&RT Training process ：

function DecisionTree$($ data $\mathcal{D}={\left\{\left({\mathbf{x}}_n,y_n\right)\right\}}_{n=1}^N)$

if cannot branch anymore

​ return $g_t(\mathbf{x})=E_{\text{in }}$ -optimal constant

else

​ 1、 learn branch criteria：（ This step is to traverse all the values of all the features ）
$$b(\mathbf{x})=\underset{\text{ decision stumps }h(\mathbf{x})}{\mathrm{argmin}}\sum _{c=1}^2\mid {\mathcal{D}}_c\text{ with }h\mid \cdot \text{ impurity }\left({\mathcal{D}}_c\text{ with }h\right)$$
​ 2、 split $\mathcal{D}$ to 2 parts ${\mathcal{D}}_c=\left\{\left({\mathbf{x}}_n,y_n\right):b\left({\mathbf{x}}_n\right)=c\right\}$

​ 3、 build sub-tree $G_C\leftarrow$ DecisionTree $\left({\mathcal{D}}_C\right)$

​ 4、 return $G(\mathbf{x})={\sum }_{c=1}^2【b(\mathbf{x})=c】G_c(\mathbf{x})$

Here is the impure function （Impurity Functions） Gini coefficient is commonly used in classification tasks （Gini index）, Consider all classes , Calculated impurity ：

Classification features （Categorical Features）

In a continuous feature , The branch conditions are implemented as follows ：
$$\begin{array}{l}b(\mathbf{x})=【x_i\le \theta 】+1\\ \text{ with }\theta \in R\end{array}$$
And in discrete features , Branching conditions are similar ：
$$\begin{array}{r}b(\mathbf{x})=【x_i\in S】+1\\ \text{ with }S\subset \{1,2,\dots ,K\}\end{array}$$

Pruning regularization

If all $x_n$ Are different , that $E_{in}(G)=0$, That is to say, it is a fully grown tree , This can lead to over fitting , Because there is very little data to build in the lower subtree , So it is easy to cause over fitting . So here we think of using pruning to achieve regularization , Simply put, it is to control the number of leaves .

Use the number of leaves $\Omega (G)$ Express ：
$$\Omega (G)=\text{ NumberOfLeaves }(G)$$
Then the optimization objective after regularization is ：
$$\underset{\text{ all possible }G}{\mathrm{argmin}}{E}_{\text{in }}(G)+\lambda \Omega (G)$$
Here is a difficult question , That's it all possible $G$, It is impossible to exhaust all , stay C&RT in , The following strategies are adopted ：
$$\begin{gathered} G^{(0)}=\text{ fully-grown tree } \\ {G}^{(i)}={\mathrm{argmin}}_G{E}_{\text{in }}(G)\text{ such that }G\text{ is one-leaf removed from }{G}^{(i-1)} \end{gathered}$$
That is to say, it is removing $ i $sliceTreesleafOf"StrategyTreesinlook\; forOutsexcanmostoptimalOfOnestar,The"StrategyTreesfrompickfall$i−1 $sliceTreesleafOf"StrategyTreesinmostoptimalOfOnestarAgainpickfallOnesliceahave\; to.thatWellfalseset\; upEndwholeLongbecomeOf"StrategyTreesOfleafSonCountThe\; amountby$I$, So now you can get ：

$$G^{(0)},G^{(1)},\cdots ,G^{\left(I^{-}\right)}\text{ where }{I}^{-}\le I$$
So from this pile $G^{(i)}$ Use in Optimization objective of regularization Find the optimal decision tree .

Random forests （Random Forest）

Fully grown into a tree （fully-grown C&RT decision tree） The disadvantage of is the large variance , and bagging The function of is to reduce the variance , The essence of random forest is to combine the two .
$$\text{ random forest }(\mathrm{R}\mathrm{F})=\text{ bagging }+\text{ fully-grown C\&RT decision tree }$$
The random forest is made up of several trees CART form , The core is “ Two random ”.

Two random + No pruning

Random forest is random in two random ：

Random sampling （bootstrap sampling）

If the training set size is N, For every tree , Randomly and put back from the training set N Training samples （bootstrap sample）, As the training set of the tree ; From here we can know ： The training set of each tree is different , And it contains repeated training samples .

Randomly selected features

If the characteristic dimension of each sample is $M$, Specify a constant $m<<M$, Randomly from $M$ Selected from features $m$ A subset of features , Every time a tree splits , From here $m$ Choose the best of the features .

In other words, it is equivalent to making predictions in a subspace of sample features each time . for instance , Watermelon classification ,RF Each tree in the tree is based on a feature such as color 、 Pattern to do classification .

No pruning

Every tree is fully grown , No pruning . In this way, a single tree may be over fitted , But the diversity of each tree is good 、 Low tree to tree correlation , So the whole forest is not easy to be fitted .

Random forest classification effect （ Error rate ） It's related to two factors ：

• The correlation of any two trees in the forest ： The more relevant , The higher the error rate
• The ability to classify every tree in the forest ： The stronger the ability of each tree to classify , The lower the error rate of the whole forest .

Reduce the number of feature selections m, Tree correlation and classification ability will also be reduced accordingly ; increase m, The two will increase as well . So the key question is how to choose the best m（ Or the scope ）, This is also the only parameter of random forest .

OOB Error

One advantage of random forest is that there is no need to reserve a validation data set , stay bootstrap sampling In the process of , The probability that a sample will not be sampled is about one third , So for every tree , Yes 1/3 Of the samples did not participate in the training , these OOB The sample is a natural validation set .OOB Error Estimation method of ：

1. Traversing all samples , For each sample , Calculate it as OOB Sample tree Classification of the sample .（ about 1/3 The tree of ）
2. Then a simple majority vote is taken as the classification result of the sample ;
3. Finally, the ratio of the number of misclassification to the total number of samples is used as the random forest oob Misclassification rate .

oob The error rate is an unbiased estimate of the generalization error of random forest , Its result is similar to that which needs a lot of calculation k Crossover verification .