当前位置:网站首页>[combinatorics] generating function (property summary | important generating function)*
[combinatorics] generating function (property summary | important generating function)*
2022-07-03 17:55:00 【Programmer community】
List of articles
- One 、 Summary of generated function properties
- Two 、 Generate the correspondence between the function and the sequence
Reference blog :
- 【 Combinatorial mathematics 】 Generating function Brief introduction ( Generating function definition | Newton's binomial coefficient | Common generating functions | Related to constants | Related to binomial coefficient | Related to polynomial coefficients )
- 【 Combinatorial mathematics 】 Generating function ( Linear properties | Product properties )
- 【 Combinatorial mathematics 】 Generating function ( Shift property )
- 【 Combinatorial mathematics 】 Generating function ( The nature of summation )
- 【 Combinatorial mathematics 】 Generating function ( Commutative properties | Derivative property | Integral properties )
One 、 Summary of generated function properties
1 . Generating function Linear properties :
Multiplication :
b
n
=
α
a
n
b_n = \alpha a_n
bn=αan , be
B
(
x
)
=
α
A
(
x
)
B(x) = \alpha A(x)
B(x)=αA(x)
Add :
c
n
=
a
n
+
b
n
c_n = a_n + b_n
cn=an+bn , be
C
(
x
)
=
A
(
x
)
+
B
(
x
)
C(x) = A(x) + B(x)
C(x)=A(x)+B(x)
2 . Shift property of generating function :
To shift backward :
b
(
n
)
=
{
0
,
n
<
l
a
n
−
l
,
n
≥
l
b(n) = \begin{cases} 0, & n < l \\\\ a_{n-l}, & n \geq l \end{cases}
b(n)=⎩⎪⎨⎪⎧0,an−l,n<ln≥l , be
B
(
x
)
=
x
l
A
(
x
)
B(x) = x^l A(x)
B(x)=xlA(x)
Forward shift :
b
n
=
a
n
+
1
b_n = a_{n+1}
bn=an+1 , be
B
(
x
)
=
A
(
x
)
−
∑
n
=
0
l
−
1
a
n
x
n
x
l
B(x) = \cfrac{A(x) - \sum\limits_{n=0}^{l-1} a_nx^n }{x^l}
B(x)=xlA(x)−n=0∑l−1anxn
3 . Generating function Product properties :
c
n
=
∑
i
=
0
n
a
i
b
n
−
i
c_n = \sum\limits_{i=0}^n a_i b_{n-i}
cn=i=0∑naibn−i , Then there are
C
(
x
)
=
A
(
x
)
⋅
B
(
x
)
C(x) = A(x) \cdot B(x)
C(x)=A(x)⋅B(x)
Summation property of generating function :
Sum forward :
b
n
=
∑
i
=
0
n
a
i
b_n = \sum\limits_{i=0}^{n}a_i
bn=i=0∑nai , be
B
(
x
)
=
A
(
x
)
1
−
x
B(x) = \cfrac{A(x)}{1-x}
B(x)=1−xA(x)
Backward summation :
b
n
=
∑
i
=
n
∞
a
i
b_n = \sum\limits_{i=n}^{\infty}a_i
bn=i=n∑∞ai , also
A
(
1
)
=
∑
i
=
n
∞
a
i
A(1) =\sum\limits_{i=n}^{\infty}a_i
A(1)=i=n∑∞ai convergence , be
B
(
x
)
=
A
(
1
)
−
x
A
(
x
)
1
−
x
B(x) = \cfrac{A(1) - xA(x)}{1-x}
B(x)=1−xA(1)−xA(x)
4 . The commutative property of generating function :
b
n
=
α
n
a
n
b_n = \alpha^n a_n
bn=αnan , be
B
(
x
)
=
A
(
α
x
)
B(x) =A( \alpha x)
B(x)=A(αx)
5 . Derivation property of generating function :
b
n
=
n
a
n
b_n = n a_n
bn=nan , be
B
(
x
)
=
x
A
′
(
x
)
B(x) =xA'( x)
B(x)=xA′(x)
6 . Integral property of generating function :
b
n
=
a
n
n
+
1
b_n = \cfrac{a_n}{n+1}
bn=n+1an , be
B
(
x
)
=
1
x
∫
0
x
A
(
x
)
d
x
B(x) =\cfrac{1}{x} \int^{x}_{0} A( x)dx
B(x)=x1∫0xA(x)dx
Two 、 Generate the correspondence between the function and the sequence
Given sequence
{
a
n
}
\{a_n\}
{ an} or
a
n
a_n
an The recursion equation of , Find the generating function
G
(
x
)
G(x)
G(x) , We need to use the properties of series and Some important series ;
Commonly used generation function values :
1
1
1 Sequence correlation :
{
a
n
}
\{a_n\}
{ an} ,
a
n
=
1
n
a_n = 1^n
an=1n ;
A
(
x
)
=
∑
n
=
0
∞
x
n
=
1
1
−
x
\begin{aligned} A(x) & = \sum_{n=0}^{\infty} x^n = \frac{1}{1-x} \end{aligned}
A(x)=n=0∑∞xn=1−x1
{
a
n
}
\{a_n\}
{ an} ,
a
n
=
(
−
1
)
n
a_n = (-1)^n
an=(−1)n ;
A
(
x
)
=
∑
n
=
0
∞
(
−
1
)
n
x
n
=
1
1
+
x
\begin{aligned} A(x) & = \sum_{n=0}^{\infty} (-1)^n x^n = \frac{1}{1+x} \end{aligned}
A(x)=n=0∑∞(−1)nxn=1+x1
{
a
n
}
\{a_n\}
{ an} ,
a
n
=
k
n
a_n = k^n
an=kn ,
k
k
k As a positive integer ;
A
(
x
)
=
∑
n
=
0
∞
k
n
x
n
=
1
1
−
k
x
\begin{aligned} A(x) & = \sum_{n=0}^{\infty} k^n x^n = \frac{1}{1-kx} \end{aligned}
A(x)=n=0∑∞knxn=1−kx1
Binomial coefficient correlation :
{
a
n
}
\{a_n\}
{ an} ,
a
n
=
(
m
n
)
a_n = \dbinom{m}{n}
an=(nm) ;
A
(
x
)
=
∑
n
=
0
∞
(
m
n
)
x
n
=
(
1
+
x
)
m
\begin{aligned} A(x) & = \sum_{n=0}^{\infty} \dbinom{m}{n} x^n = ( 1 + x ) ^m \end{aligned}
A(x)=n=0∑∞(nm)xn=(1+x)m
Combination number correlation :
{
a
n
}
\{a_n\}
{ an} ,
a
n
=
(
m
+
n
−
1
n
)
a_n = \dbinom{m+n-1}{n}
an=(nm+n−1) ,
m
,
n
m,n
m,n As a positive integer ;
A
(
x
)
=
∑
n
=
0
∞
(
m
+
n
−
1
n
)
x
n
=
1
(
1
−
x
)
m
\begin{aligned} A(x) & = \sum_{n=0}^{\infty} \dbinom{m+n-1}{n} x^n = \frac{1}{ {(1-x)}^m} \end{aligned}
A(x)=n=0∑∞(nm+n−1)xn=(1−x)m1
{
a
n
}
\{a_n\}
{ an} ,
a
n
=
(
−
1
)
n
(
m
+
n
−
1
n
)
a_n = (-1)^n \dbinom{m+n-1}{n}
an=(−1)n(nm+n−1) ,
m
,
n
m,n
m,n As a positive integer ;
A
(
x
)
=
∑
n
=
0
∞
(
−
1
)
n
(
m
+
n
−
1
n
)
x
n
=
1
(
1
+
x
)
m
\begin{aligned} A(x) & = \sum_{n=0}^{\infty} (-1)^n \dbinom{m+n-1}{n} x^n = \frac{1}{ {(1+x)}^m} \end{aligned}
A(x)=n=0∑∞(−1)n(nm+n−1)xn=(1+x)m1
{
a
n
}
\{a_n\}
{ an} ,
a
n
=
(
n
+
1
n
)
a_n = \dbinom{n+1}{n}
an=(nn+1) ,
n
n
n As a positive integer ;
A
(
x
)
=
∑
n
=
0
∞
(
n
+
1
n
)
x
n
=
∑
n
=
0
∞
(
n
+
1
)
x
n
=
1
(
1
−
x
)
2
\begin{aligned} A(x) & = \sum_{n=0}^{\infty} \dbinom{n+1}{n} x^n \\ & = \sum_{n=0}^{\infty} (n+1) x^n \\ & = \frac{1}{ {(1-x)}^2} \end{aligned}
A(x)=n=0∑∞(nn+1)xn=n=0∑∞(n+1)xn=(1−x)21
边栏推荐
- WebView module manages the application window interface to realize the logical control and management operation of multiple windows (Part 1)
- [Tongxin UOS] scanner device management driver installation
- [combinatorics] recursive equation (four cases where the non-homogeneous part of a linear non-homogeneous recursive equation with constant coefficients is the general solution of the combination of po
- How to enforce parameters in PowerShell- How do I make parameters mandatory in PowerShell?
- 1147_ Makefile learning_ Target files and dependent files in makefile
- PHP MySQL preprocessing statement
- Investigation on the operation prospect of the global and Chinese Anti enkephalinase market and analysis report on the investment strategy of the 14th five year plan 2022-2028
- 远程办公工具分享|社区征文
- Kotlin's collaboration: Context
- link preload prefetch
猜你喜欢
Records of long objects and long judgments in the stream of list

Research Report on investment trends and development planning of China's thermal insulation material industry, 2022-2028

TCP congestion control details | 3 design space

(9) Opencv Canny edge detection

PHP MySQL create database
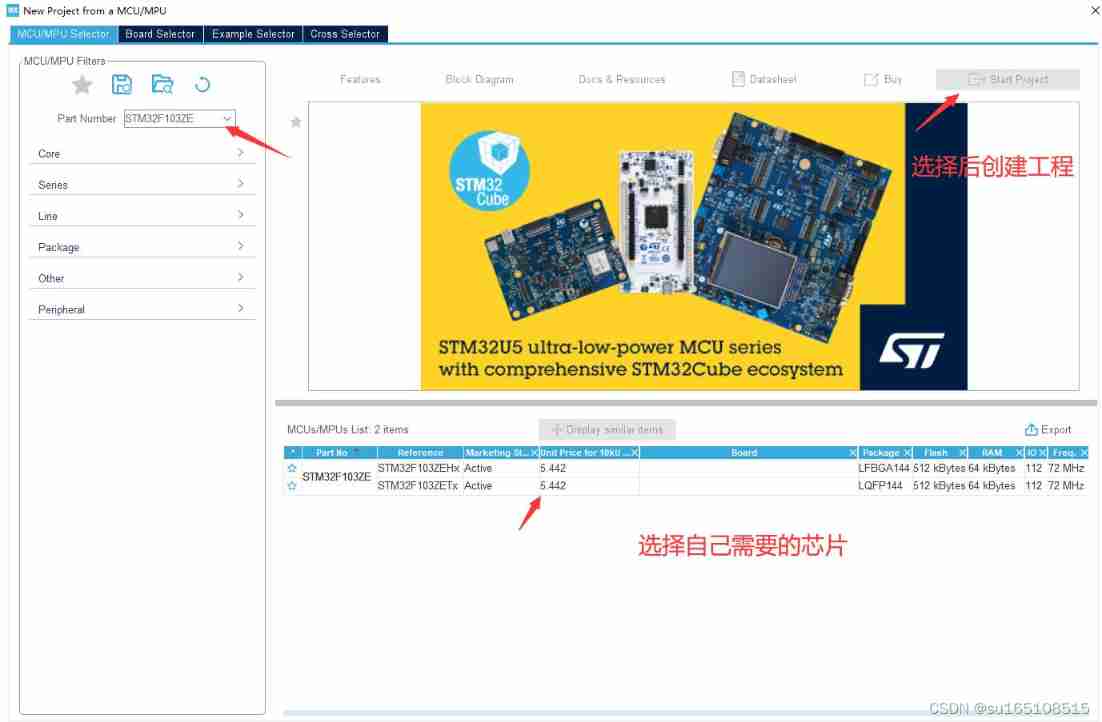
Baiwen.com 7 days Internet of things smart home learning experience punch in the next day
AcWing 271. 杨老师的照相排列【多维DP】

一入“远程”终不悔,几人欢喜几人愁。| 社区征文
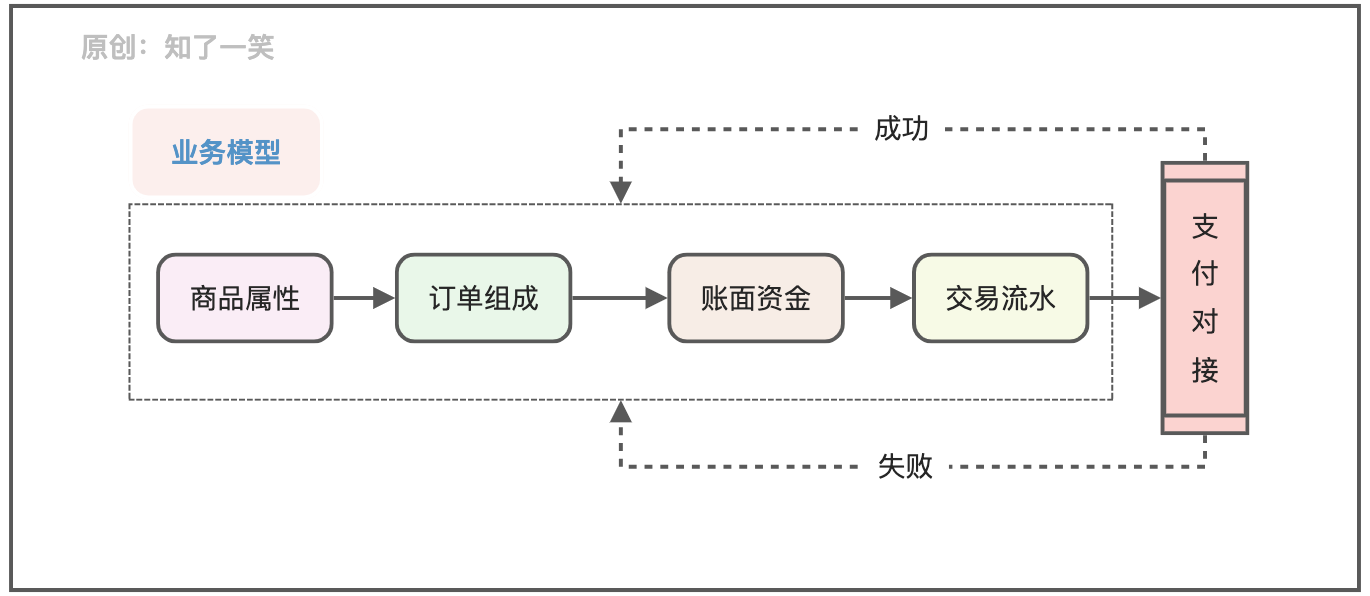
聊聊支付流程的设计与实现逻辑

Line by line explanation of yolox source code of anchor free series network (5) -- mosaic data enhancement and mathematical understanding
随机推荐
PUT vs. POST for Uploading Files - RESTful API to be Built Using Zend Framework
Internet hospital his management platform source code, online consultation, appointment registration smart hospital applet source code
Introduction to PHP MySQL
Kotlin的協程:上下文
Implementation of Tetris in C language
Kotlin的协程:上下文
Keepalived 设置不抢占资源
AcWing 4489. Longest subsequence
Codeforces Round #803 (Div. 2) C. 3SUM Closure
Ml (machine learning) softmax function to realize the classification of simple movie categories
[combinatorics] generating function (linear property | product property)
c# . Net tool ecosystem
Write a program to process a list container of string type. Find a special value in the container 9.27: and delete it if found. Rewrite the above procedure with deque container.
PHP MySQL preprocessing statement
Deops入门
1147_ Makefile learning_ Target files and dependent files in makefile
Kotlin's collaboration: Context
Investigation on the operation prospect of the global and Chinese Anti enkephalinase market and analysis report on the investment strategy of the 14th five year plan 2022-2028
Life perception 1
How to enforce parameters in PowerShell- How do I make parameters mandatory in PowerShell?