2022杭电多校3

T1009 Package Delivery

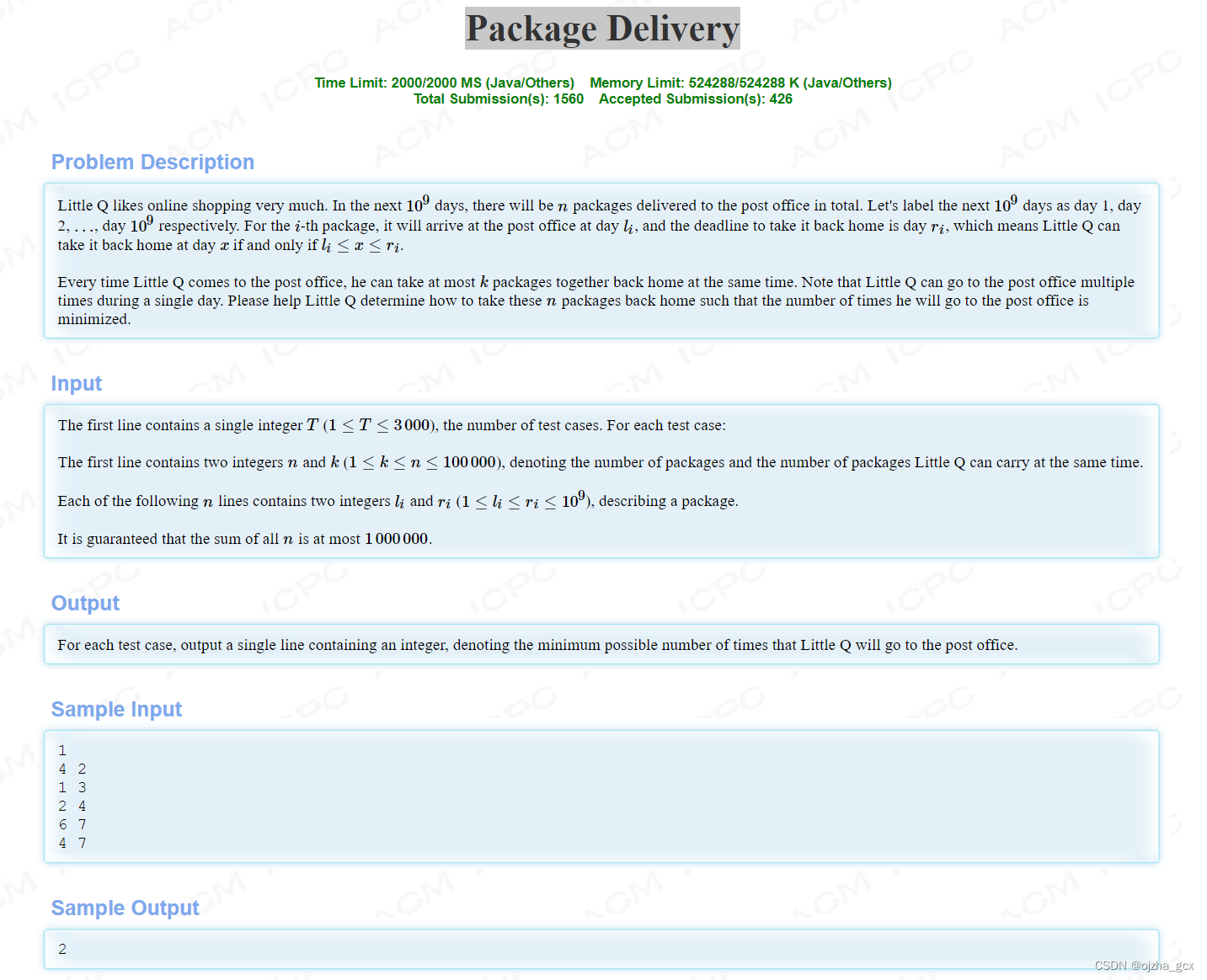
题意：给定n和k，n代表快递个数，k代表一次最多能拿的快递数，接下来n行每行给出两个数，分别代表快递的到达时间以及截至时间，我们必须要在截止时间之前把快递取走，一天可以取多次快递，问我们取完所有的快递至少需要取的次数。

iidea：我们可以尽量把取快递的时间往后延，这样我们相应地一次取出来的快递数也可能会更多，我们只在截至时间取快递，我们一次尽可能地多取快递，首先我们需要先对所有的快递按照开始时间$l$从小到大排序，然后遍历一遍，我们可以设置一个时间t代表我们当前的时间点，我们用一个队列记录当前时间已经到达且还未取出的快递，则所有$l<t$的快递都应该被加入到队列中（还未取出的快递），这个队列按照结束时间$r$升序排列，因为当$t$等于一个快递的截至时间时我们必须要花费一次把他取出。

当t到达一个快递的结束时间时队列中的快递数目有两种情况：
1.小于等于k个，那我们直接全部取出即可
2.大于k个，那么我们就把r从小到达取出k个即可（即使没有取完也只取k个）

之所以当快递数大于k个时我们不把它全部取完是因为我们先把必须要取的取了，那么剩余的快递如果还没有到达截至时间，我们可以稍微等等，之后或许可以与其他后到的快递一起取出，这样答案或许会更优。

#include<bits/stdc++.h>
#define LL long long
#define MIN 0xc0c0c0c0c0c0c0c0
#define PII pair<LL,LL>
#define x first
#define y second
using namespace std;

const LL N = 4e5+100;
LL n,k;
PII a[N];
priority_queue< PII , vector<PII> , greater<PII> > q;

void solve()
{
    
	LL ans = 0;
	scanf("%lld %lld",&n,&k);
	for(int i=1;i<=n;i++)
	{
    
		scanf("%lld %lld",&a[i].x,&a[i].y);
	}
	sort( a+1,a+n+1 );
	while( !q.empty() ) q.pop();
	q.push( {
     a[1].y,a[1].x } );
	LL t = a[1].y;
	for(int i=2;i<=n;)
	{
    
		while( i<=n && ( t==-1 || a[i].x<=t ) )
		{
    
			q.push( {
     a[i].y,a[i].x } );
			if( t==-1 ) t = a[i].y;
			else t = min( t,a[i].y );
			i++;
		}
		if( q.size()<=k ){
    
			ans++;
			while( !q.empty() ) q.pop();
			t = -1;
		}
		else if(q.size()>0){
    
			LL h = k;
			ans++;
			while( h-- ) q.pop();
			t = q.top().first;
		}
	}
	ans += ( ( q.size()+k-1 )/k );
	printf("%lld\n",ans);
}

int main()
{
    
	#ifndef ONLINE_JUDGE
	freopen("in.txt","r",stdin);
	#endif
	int t;
	cin>>t;
	while( t-- )
	solve();
	return 0;
}

T1011 Taxi

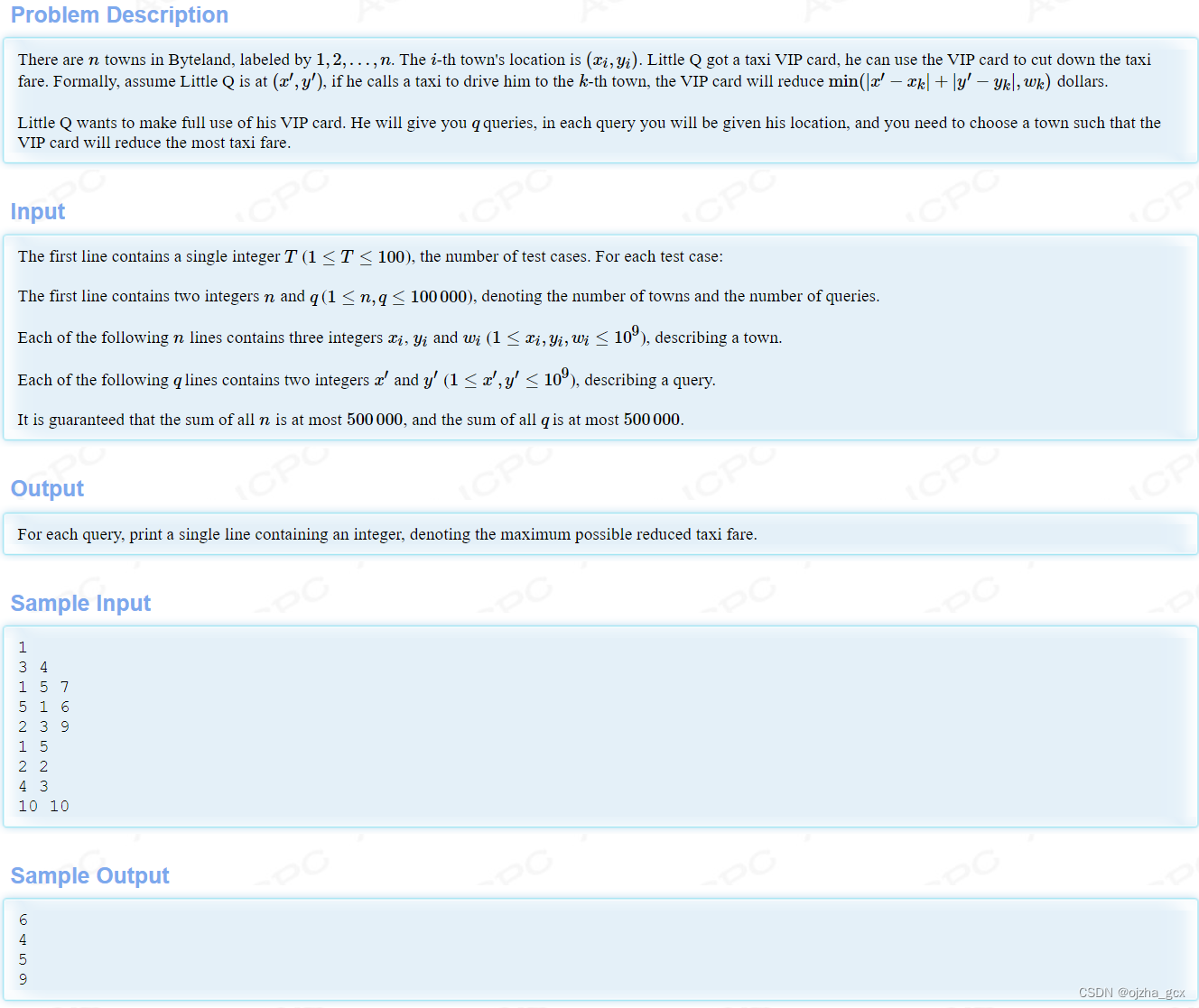
题意：给定n个城市，q个询问,第k个城市有一个属性$w_k$，对于每一个询问q给定一个点$(x,y)$，这个点到第k个城市$(x_i,y_i)$的距离是$dist=min(|x-x_k|+|y-y_k|,w_k)$，问这个点到n个城市中$dist$最大值是多少。

idea：式子中的$|x-x_k|+|y-y_k|$要同时考虑两维的限制，对于这个曼哈顿距离我们可以转成切比雪夫距离。关于切比雪夫距离推荐看这个大佬的博客。

1. 首先考虑没有$w_k$限制的情况，其实这就是经典的切比雪夫的套路，把点$(x_i,y_i)$变成$(x_i+y_i,x_i-y_i)$，这样转换后的点之间的切比雪夫距离就是原图中的哈夫曼距离。那么求答案就变成了求$max(|x^{{}^{\prime }}-x_k^{{}^{\prime }}|,|y^{{}^{\prime }}-y_k^{{}^{\prime }}|)$这其实就是在$x^{{}^{\prime }}-x_k^{{}^{\prime }},x_k^{{}^{\prime }}-x^{{}^{\prime }},y^{{}^{\prime }}-y_k^{{}^{\prime }},y_k^{{}^{\prime }}-y^{{}^{\prime }}$四个值之间取最max值。分别记录 $x_k^{{}^{\prime }},-x_k^{{}^{\prime }},y_k^{{}^{\prime }},-y_k^{{}^{\prime }}$ 的最大值即可在 O(1) 时间内求出所有点到给定点切比雪夫距离的最大值。

2.现在考虑加入 $w_k$ 的限制。将所有城镇按照 $w_k$ 从小到大排序，并记录排序后每个后缀的$x_k^{{}^{\prime }},-x_k^{{}^{\prime }},y_k^{{}^{\prime }},-y_k^{{}^{\prime }}$ 的最大值，用于 O(1) 求给定点 到该后缀中所有点的距离最大值。选取按 $w_k$ 排序后的第 k 个城镇，可以O(1) 求出给给定点到第 k…n 个城镇的距离最大值d，有两种情况：
（1）$w_k<d$，那么第 $k..n$ 个城镇对答案的贡献至少为$w_k$。用$w_k$ 更新答案后，由于第 $\mathrm{1..}k$ 个
城镇的 $w$ 值均不超过 $w_k$，因此它们不可能接着更新答案，考虑范围缩小至 $[k+1,n]$。
(2) $w_k\ge d$，那么第 $k..n$ 个城镇对答案的贡献为 $d$。用 $d$ 更新答案后，考虑范围缩小至$[1,k-1]$。
容易发现每次考虑的范围都是一个区间，如果每次取 k 为区间的中点，那么二分迭代 O(log n)次即可得到最优解。

#include<bits/stdc++.h>
#define LL long long
#define MIN 0xc0c0c0c0c0c0c0c0
using namespace std;

const LL N = 1e5+100;
LL n,m;

struct point
{
    
	LL x,y,w;
}e[101010];
bool cmp(point a,point b)
{
    
	return a.w<b.w;
}
LL a[N],b[N],c[N],d[N];

void solve()
{
    
	LL p,q,k,xx,yy;
	scanf("%lld %lld",&n,&m);
	for(int i=1;i<=n;i++)
	{
    
		scanf("%lld %lld %lld",&p,&q,&k);
		e[i].x = p+q;
		e[i].y = p-q;
		e[i].w = k;		
	}
	sort( e+1,e+n+1,cmp );
	a[n+1] = b[n+1] = c[n+1] = d[n+1] = MIN;
	for(int i=n;i>=1;i--)
	{
    
		a[i] = max( a[i+1] , -e[i].x );
		b[i] = max( b[i+1] , e[i].x );
		c[i] = max( c[i+1] , -e[i].y );
		d[i] = max( d[i+1] , e[i].y );
	}
	while( m-- )
	{
    
		LL ans = 0,temp;
		scanf("%lld %lld",&p,&q);
		xx = p+q,yy = p-q;
		LL l = 1,r = n;
		while( l<=r )
		{
    
			LL mid = (l+r)>>1;
			temp = xx + a[mid];
			temp = max( temp , b[mid] - xx );
			temp = max( temp , yy+c[mid] );
			temp = max( temp , d[mid]-yy );
			if( temp>=e[mid].w )
			{
    
				l = mid+1;
				ans = max( ans,e[mid].w );
			}
			else 
			{
    
				r=  mid-1;
				ans = max( ans,temp );
			}
		}
		printf("%lld\n",ans);
	}
}

int main()
{
    
	#ifndef ONLINE_JUDGE
	freopen("in.txt","r",stdin);
	#endif
	int t;
	cin>>t;
	while( t-- )
	solve();
	return 0;
}