当前位置:网站首页>leetcode:255 验证前序遍历序列二叉搜索树
leetcode:255 验证前序遍历序列二叉搜索树
2022-08-04 14:31:00 【OceanStar的学习笔记】
题目来源
题目描述
给定一个整数数组,你需要验证它是否是一个二叉搜索树正确的先序遍历序列。
你可以假定该序列中的数都是不相同的。
参考以下这颗二叉搜索树:

示例 1:
输入: [5,2,6,1,3]
输出: false
示例 2:
输入: [5,2,1,3,6]
输出: true
题目解析
思路
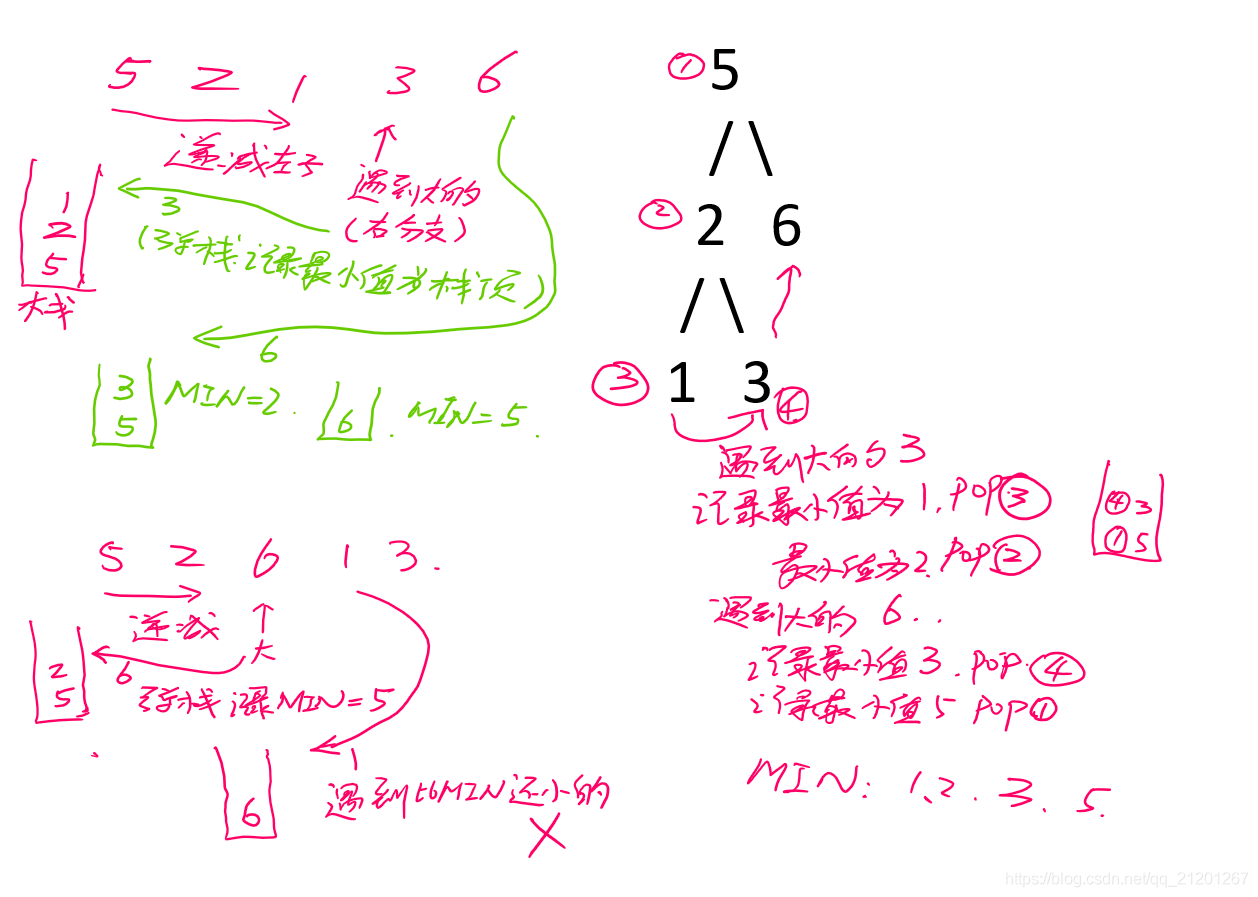
- 二叉搜索树的特点是: 左子树的值 < 根节点的值 < 右子树的值
- 所以其中序遍历一定是有序数组,但是前序遍历有什么规律呢?其前序遍历的数组是局部递减,整体递增的数组
- 所以可以借助单调栈
- 先设一个最小值 low,然后遍历数组,如果当前值小于这个最小值 low,返回 false
- 对于根节点,将其压入栈中,然后往后遍历
- 如果遇到的数字比栈顶元素小,说明是其左子树的点,继续压入栈中
- 直到遇到的数字比栈顶元素大,那么就是右边的值了。需要找到是哪个节点的右子树,所以更新 low 值并删掉栈顶元素,然后继续和下一个栈顶元素比较,如果还是大于,则继续更新 low 值和删掉栈顶,直到栈为空或者当前栈顶元素大于当前值停止,压入当前值
- 这样如果遍历完整个数组之前都没有返回 false 的话,最后返回 true 即可
class Solution {
public:
bool verifyPreorder(vector<int>& preorder) {
if(preorder.size() <= 2) return true;
int MIN = INT32_MIN;
stack<int> s;
for(int i = 0; i < preorder.size(); ++i)
{
if(preorder[i] < MIN)
return false;
while(!s.empty() && s.top() < preorder[i])//遇到大的了,右分支
{
MIN = s.top();//记录弹栈的栈顶为最小值
s.pop();
}
s.push(preorder[i]);
}
return true;
}
};
进阶要求
为了使空间复杂度为常量,我们不能使用 stack,所以直接修改 preorder,将 low 值存在 preorder 的特定位置即可
class Solution {
public:
bool verifyPreorder(vector<int>& preorder) {
int low = INT_MIN, i = -1;
for (auto a : preorder) {
if (a < low) return false;
while (i >= 0 && a > preorder[i]) {
low = preorder[i--];
}
preorder[++i] = a;
}
return true;
}
};
分治法
- 在递归函数中维护一个下界 lower 和上界 upper,那么当前遍历到的节点必须在(low, upper)之间
- 然后在给定区间内搜索第一个>=当前值的点,以此为分界点,左右两边分别调用递归函数。注意左半部分的 upper 更新为当前节点值 val,表明左子树的节点值都必须小于当前节点值,而右半部分的递归的 lower 更新为当前节点值 val,表明右子树的节点值都必须大于当前节点值
- 如果左右两部分的返回结果均为真,则整体返回真
class Solution {
public:
bool verifyPreorder(vector<int>& preorder) {
return helper(preorder, 0, preorder.size() - 1, INT_MIN, INT_MAX);
}
bool helper(vector<int>& preorder, int start, int end, int lower, int upper) {
if (start > end) return true;
int val = preorder[start], i = 0;
if (val <= lower || val >= upper) return false;
for (i = start + 1; i <= end; ++i) {
if (preorder[i] >= val) break;
}
return helper(preorder, start + 1, i - 1, lower, val) && helper(preorder, i, end, val, upper);
}
};
边栏推荐
- ICML 2022 | 图神经网络的局部增强
- 手搓一个“七夕限定”,用3D Engine 5分钟实现烟花绽放效果
- CCF GLCC officially opened | Kyushu Cloud open source experts bring generous bonuses to help universities promote open source
- 基于 Next.js实现在线Excel
- Win11勒索软件防护怎么打开?Win11安全中心勒索软件防护如何设置
- 1403. 非递增顺序的最小子序列
- License server system does not support this version of this feature
- [机缘参悟-60]:《兵者,诡道也》-1-开篇:“死“与“生“都是天道
- 理论篇1:深度学习之----LetNet模型详解
- 企业级优化
猜你喜欢
基于 Next.js实现在线Excel
CCF GLCC正式开营|九州云开源专家携丰厚奖金,助力高校开源推广
Fuse bit of AVR study notes

技术分享| 融合调度系统中的电子围栏功能说明
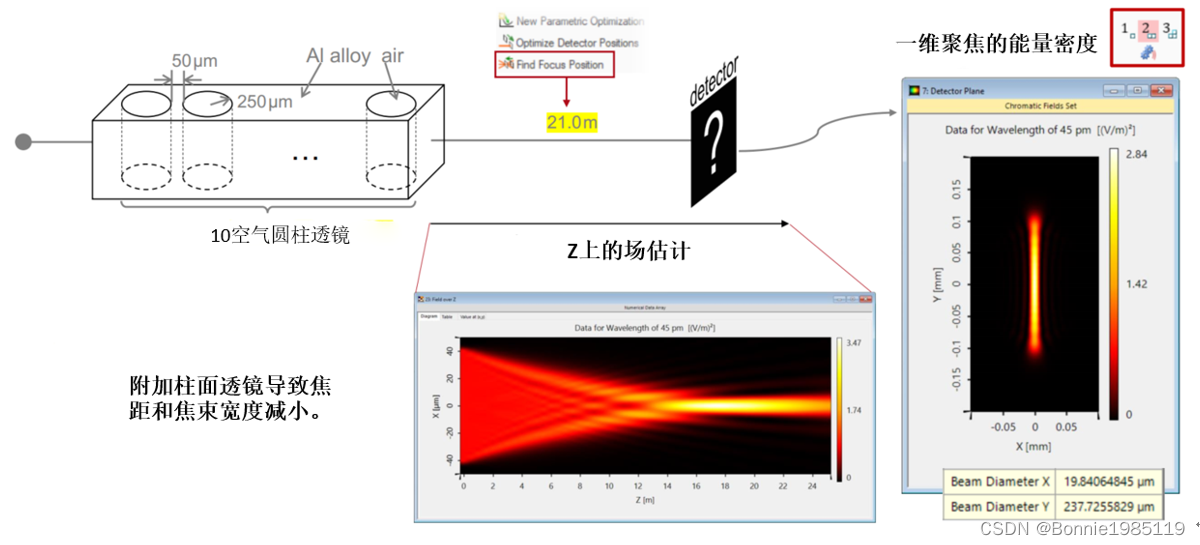
用于X射线聚焦的复合折射透镜
爬虫——selenium基本使用、无界面浏览器、selenium的其他用法、selenium的cookie、爬虫案例

属于程序猿的浪漫

化算力为战力:宁夏中卫的数字化转型启示录

自监督学习未来是掩码自编码器?KAIST最新《自监督学习掩码自编码器》研究进展
Google plug-in. Download contents file is automatically deleted after solution
随机推荐
节省50%成本!京东云重磅发布新一代混合CDN产品
量化细胞内的信息流:机器学习时代下的研究进展
自监督学习未来是掩码自编码器?KAIST最新《自监督学习掩码自编码器》研究进展
Qt的QItemDelegate使用
Kyushu Cloud attended the Navigator Online Forum to discuss the current status, challenges and future of 5G MEC edge computing
Convolutional Neural Network Basics
【模型部署与业务落地】基于量化芯片的损失分析
职场漫谈:为什么越是内卷的行业越有人争着抢着往里冲?好奇怪的说...
C# 复制列表
C# winforms 输入颜色转换颜色名
技术分享| 小程序实现音视频通话
B. Construct a simple sequence (greedy)
如何和程序员谈恋爱
期货开户之前要谈好最低手续费和交返
杭电校赛(ACM组队安排)
FRED应用:毛细管电泳系统
xampp安装包含的组件有(php,perl,apche,mysql)
[LeetCode] 38. Appearance sequence
利用决策树找出最优特征组合
Keycloak 6.0.0 正式发布,身份和访问管理系统