四平方和，激光炸弹

四平方和(简单）

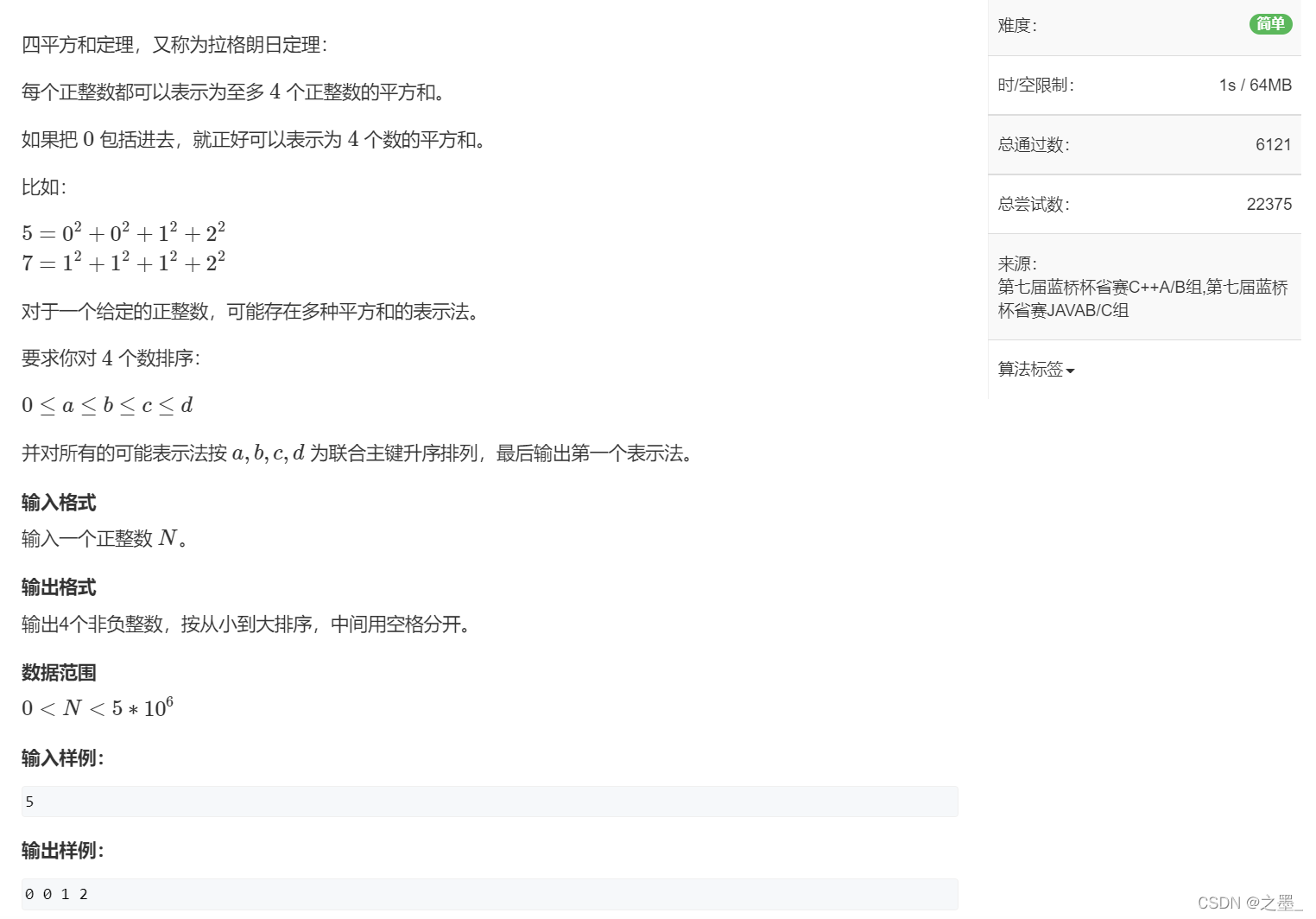
三层暴力遍历，再对最后一个数用平方求是否满足正整数的要求，有数据超时

#include <iostream>
#include <stdio.h>
#include <cmath>
using namespace std;

const int N = 5e6;
int n;
int a[N];
int main(){
    
    int a,b,c,d;
    scanf("%d",&n);
    for(int a = 0;a*a <= n;a++)
        for(int b = a;a*a+b*b <= n;b++)
            for(int c = b;a*a+b*b+c*c<= n;c++)
                {
    
                    int t = n - a*a-b*b-c*c;
                    int d = sqrt(t);
                    if(d*d==t) //如果t可以表示为一个正整数的平方和
                    {
    
                        printf("%d %d %d %d",a,b,c,d);
                        return 0; 
                    }
                }
    return 0;
}

1、使用哈希表记录c d两位的记录，c*c+d*d作为哈希表的下标，存储对应的c和d，并且只会保存一组且是第一组c*c+d*d
2、将从0到n的cd组合都保存下来，再遍历0到n的ab组合,验证是否满足 n - a*a - b*b

#include<bits/stdc++.h>
using namespace std;

const int N = 1e5;
typedef pair<int,int> pii;

unordered_map<int,pii> mp;

int main(){
    
    int n;
    scanf("%d",&n);
    for(int c = 0;c*c <= n;c++)
        for(int d = c; c*c+d*d <= n;d++)
            {
       
                int t = c*c+d*d;
                if(mp.count(t) == 0)  mp[t] = {
    c,d};
            }
            
    for(int a = 0;a*a <= n;a++)
        for(int b = a;a*a+b*b <= n;b++)
        {
    
            int k = n - a*a - b*b;
            if(mp.count(k)) 
            {
    
                printf("%d %d %d %d",a,b,mp[k].first,mp[k].second);
                return 0;
            }
        }
        return 0 ;
}

但是仍然超时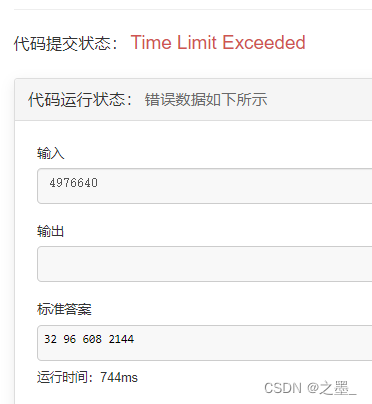

最后AC的代码 其实和上面的原理一样 使用哈希表 但是不算c++内置的 哈希表 就没超时…

#include<iostream>
#include<cmath>
using namespace std;
const int N = 1e8 + 10;
int h[N];
int main() {
    
    int n;
    cin >> n;
    //打表，找出1 - n，所有完全平方数两两之和，如果存在只记第一次出现（题目要求找出字典序小的）
    for (int i = 0; i * i * 2<= n; i++) {
    
        for (int j = i; j * j + i * i <= n; j++) {
    
            if (!h[i * i + j * j])
                h[i * i + j * j] = i + 1;//防止i = 0时在后面判断查找跳过 i = 0的情况
        }
    }
    //0<= a <= b <= c <= d,可以得出a^2 <= n / 4, a^2 + b^ 2 <= n / 2; 
    for (int i = 0; i * i * 4 <= n; i++) {
    
        for (int j = i; j * j + i * i <= n / 2; j++) {
    
            int t = n - i * i - j * j;
            if (h[t]) {
    
                int c = h[t] - 1;   
                //防止开根号后因为精度关系,向下取整,例:25 开根号得到4.99999向下取整为4;
                int d = (sqrt(t - c * c) + 1e-4);
                printf("%d %d %d %d", i, j, c, d);
                return 0;
            }
        }
    }
    return 0;
}

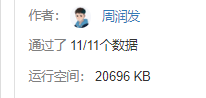
激光炸弹(简单)

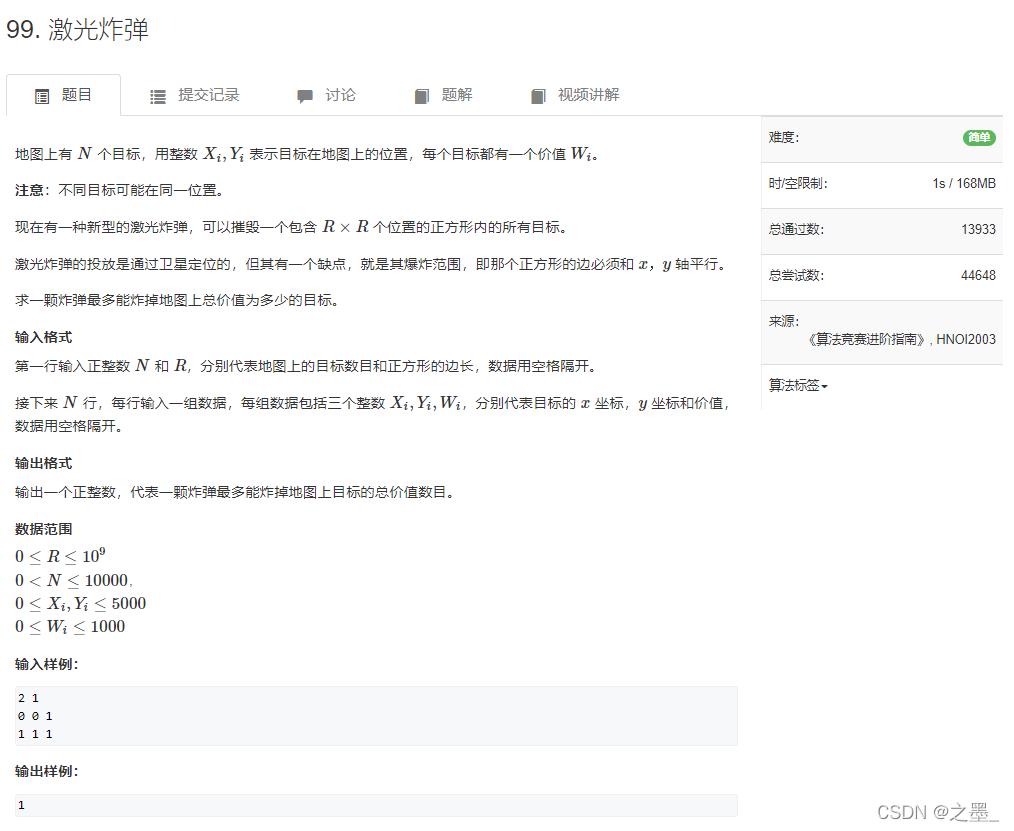
边上的点不算，这种情况是四个点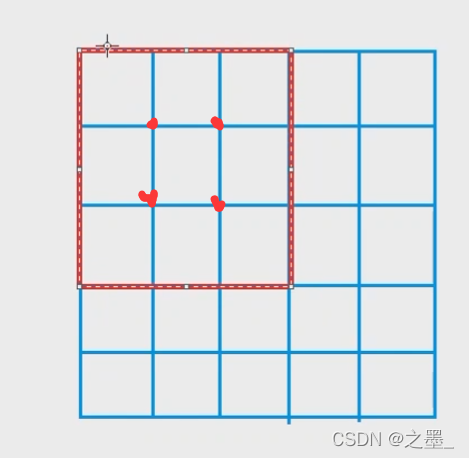

这样有9个点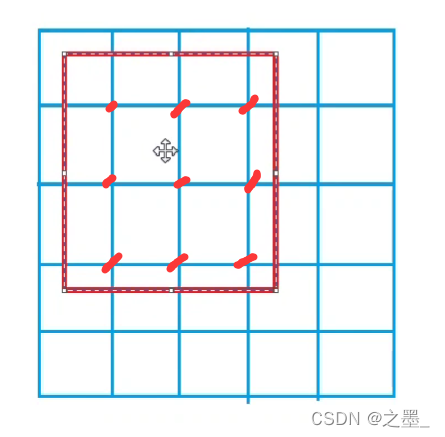

每个点的权值抽象成一个二维数组，然后求二维数组的前缀和，根据题目输入边长枚举每个满足边长的矩形的权值选出最大值

如当边长为3时，可以有一个从1,1 到 3,3的 二维矩阵 计算权值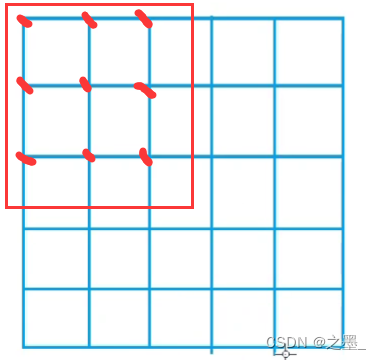

#include <stdio.h>
#include <algorithm>
using namespace std;   

const int N = 5010;
int s[N][N];
int n,r;
int mx,my;
int sum;

int main(){
    
    scanf("%d%d",&n,&r);
    r = min(5001,r);// 5001即可包括整个打击范围
    mx = my = r;
    while(n--){
    
        int x,y,w;
        scanf("%d%d%d",&x,&y,&w);
        x++;y++;//为避免边界问题 从坐标开始1,1记录
        mx = max(x,mx);my = max(y,my);//记录坐标边界
        s[x][y] += w;//记录目标权值
    }
    //记录前缀和
    for(int i = 1;i <= mx;i++)
        for(int j = 1;j <= my;j++)
            s[i][j] += s[i-1][j]+s[i][j-1]-s[i-1][j-1];


    //从右下角坐标 枚举 边长为 r 的范围 计算 权重
    for(int i = r;i <= mx;i++)
        for(int j = r;j <= my ;j++)
            sum = max(sum,s[i][j] - s[i-r][j] - s[i][j-r] + s[i-r][j-r]);

    printf("%d\n",sum);
    
    return 0;
}

K倍区间(中等)

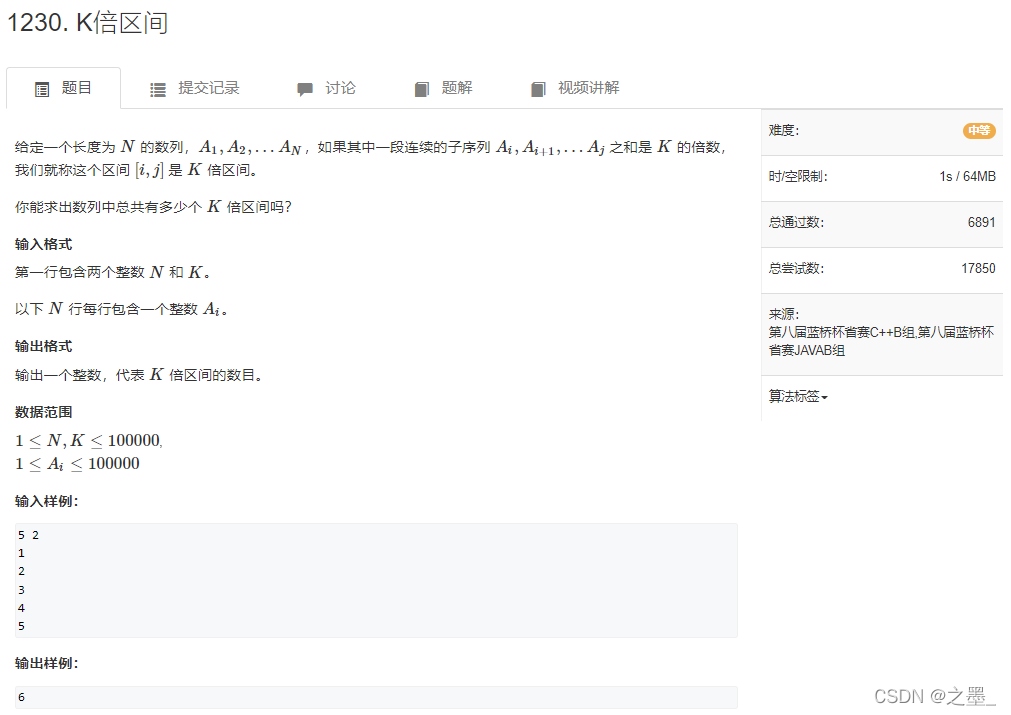
首先想到前缀和 然后暴力枚举 区间
代码很简单 但是 不出所料的超时了 这里时间复杂度貌似是O(n²)?

#include <stdio.h>

const int N = 1e5+10;
int a[N];
int n,k;
int sum;
int main(){
    
    scanf("%d%d",&n,&k);
    for(int i = 1;i <= n;i++){
    
        scanf("%d",&a[i]);
        a[i] += a[i-1];
    }
    for(int i = 1;i<=n;i++)
        for(int j = i;j<=n;j++)
             if((a[j] - a[j-i])%k == 0)
                sum++;
    printf("%d",sum);
}

接下来就需要优化代码
由前缀和可知 某个区间l - r的值等于 sum[r]- sum[l-1]
则（ sum[r] - sum[l-1]）%k = 0
可得 sum[r]%k == sum[l-1]%k
则两种情况下 存在k 倍区间

1. sum[r]%k == 0
2. 某两段前缀和模k余数相同

具体的做法就是开一个计数数组cnt[]，cnt[i]就是计算余数为i的前缀和有多少个

需要注意的是初始化 cnt[0] = 1 否则得不到正确结果

因为：

这里是用前缀和数组来算某个区间的和，前缀和数组s[0] = 0, s[i] = a[1] + a[2] + ... + a[i]，如果想算a[L] + a[L + 1] + ... + a[R]，它的值就等于s[R] - S[L - 1]，所以当L = 1的时候，就会用到s[0]了

cnt[0]存的是s[]中等于0的数的个数，由于s[0] = 0，所以最初等于0的有1个数，所以cnt[0] = 1

#include <stdio.h>

const int N = 1e5+10;
typedef long long ll;
ll a[N],cnt[N];
int n,k;
ll sum;
int main(){
    
    scanf("%d%d",&n,&k);
    for(int i = 1;i <= n;i++){
    
        scanf("%d",&a[i]);
        a[i] += a[i-1];
    }
    cnt[0]++;//cnt[] 保存的是a[]%k中值为0的个数 初始时 a[0] = 0（前缀和数组的下标0没有用到） 所以初始有一个
    for(int i = 1;i<=n;i++)
        {
    
            sum += cnt[a[i]%k];  //统计与当前值求余相同的数量
            cnt[a[i]%k]++;       // 当前值模k的数量+1
        }
    printf("%lld",sum);
}

买不到的数目(简单)

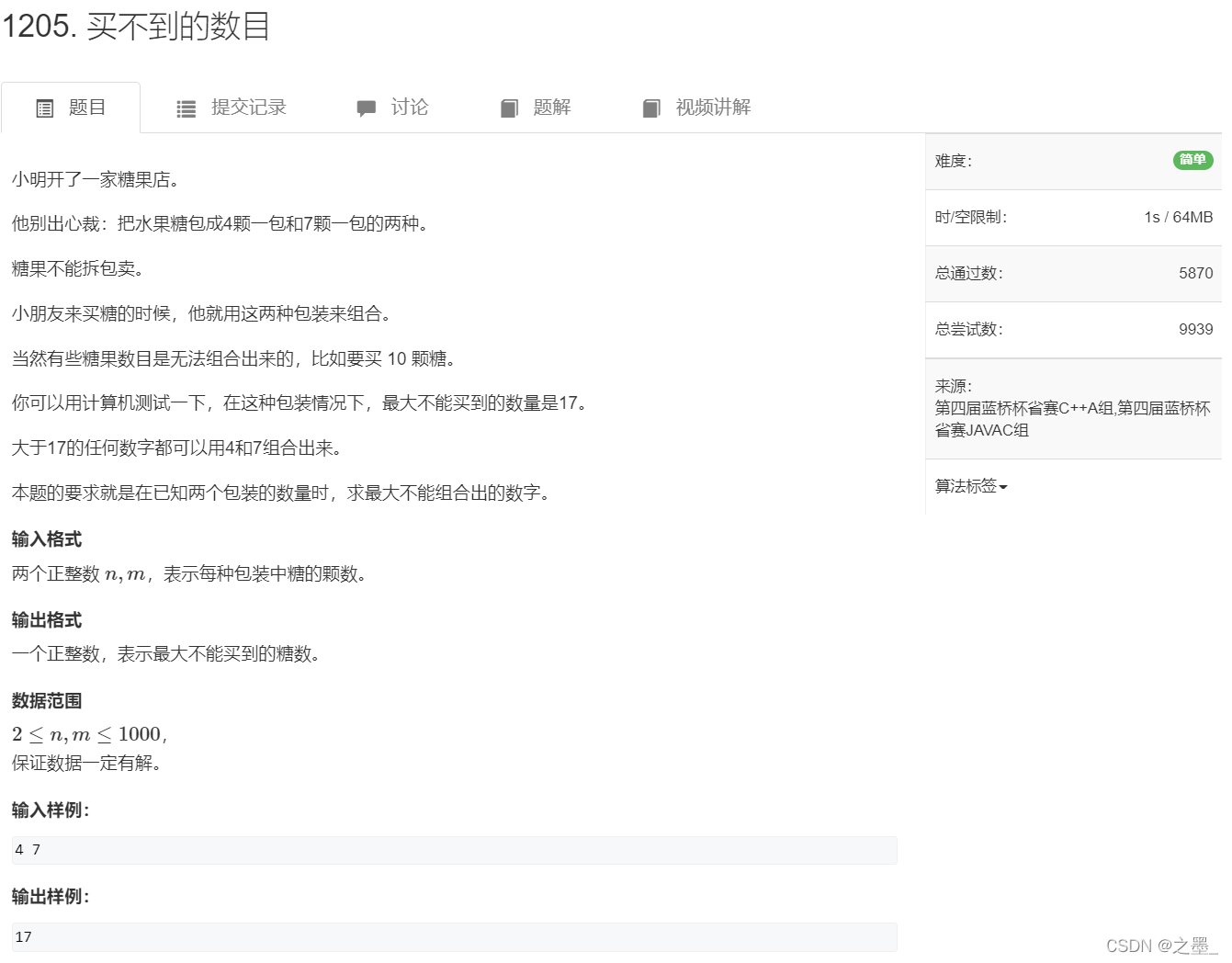
数论
裴蜀定理：对任何整数a,b和它们的最大公约数d，关于未知数x和y的线性不定方程（称为裴蜀等式）：若a,b是整数,且（a,b)=d，那么对于任意的整数x,y,ax+by都一定是d的倍数，特别地，一定存在整数x,y，使ax+by=d成立
它的一个重要推论是：a,b互质的充要条件是存在整数x,y使ax+by=1.

可以推出一个数学公式，两个互质的数 最大不能组合出的数字为 (q-1)*p-q)

#include<iostream>
using namespace std;

int p,q;

int main()
{
    
    scanf("%d%d",&p,&q);
    printf("%d\n",(q-1)*p-q);
    return 0;
}

摘花生(简单)

#include <bits/stdc++.h>

using namespace std;

const int N = 110;
int peanut[N][N],peanuts[N][N];
int t;
int main(){
    
    cin>>t;
    while(t--){
    
        int r,c;
        cin >> r >> c;
        for(int i = 1 ;i <= r; i++)
            for(int j = 1 ;j <= c ; j++)
                cin >> peanut[i][j];
        
        for(int i = 1;i <= r ; i++)
            for(int j = 1;j <= c ;j++)
                peanuts[i][j] = max(peanuts[i-1][j],peanuts[i][j-1])+peanut[i][j];
                
        cout << peanuts [r][c] <<endl;
    }
    return 0;
}