当前位置:网站首页>1375. 二进制字符串前缀一致的次数-前序遍历法
1375. 二进制字符串前缀一致的次数-前序遍历法
2022-08-04 13:49:00 【Mr Gao】
1375. 二进制字符串前缀一致的次数
给你一个长度为 n 、下标从 1 开始的二进制字符串,所有位最开始都是 0 。我们会按步翻转该二进制字符串的所有位(即,将 0 变为 1)。
给你一个下标从 1 开始的整数数组 flips ,其中 flips[i] 表示对应下标 i 的位将会在第 i 步翻转。
二进制字符串 前缀一致 需满足:在第 i 步之后,在 闭 区间 [1, i] 内的所有位都是 1 ,而其他位都是 0 。
返回二进制字符串在翻转过程中 前缀一致 的次数。
示例 1:
输入:flips = [3,2,4,1,5]
输出:2
解释:二进制字符串最开始是 “00000” 。
执行第 1 步:字符串变为 “00100” ,不属于前缀一致的情况。
执行第 2 步:字符串变为 “01100” ,不属于前缀一致的情况。
执行第 3 步:字符串变为 “01110” ,不属于前缀一致的情况。
执行第 4 步:字符串变为 “11110” ,属于前缀一致的情况。
执行第 5 步:字符串变为 “11111” ,属于前缀一致的情况。
在翻转过程中,前缀一致的次数为 2 ,所以返回 2 。
示例 2:
输入:flips = [4,1,2,3]
输出:1
解释:二进制字符串最开始是 “0000” 。
执行第 1 步:字符串变为 “0001” ,不属于前缀一致的情况。
执行第 2 步:字符串变为 “1001” ,不属于前缀一致的情况。
执行第 3 步:字符串变为 “1101” ,不属于前缀一致的情况。
执行第 4 步:字符串变为 “1111” ,属于前缀一致的情况。
在翻转过程中,前缀一致的次数为 1 ,所以返回 1 。
这题看似很复杂,千万要理解解题原理,不然暴力去求解,会花费很多时间:
int numTimesAllBlue(int* flips, int flipsSize){
int max=flips[0];
int count=0;
if(flips[0]==1){
count++;
}
for(int i=1;i<flipsSize;i++){
if(flips[i]>max){
max=flips[i];
}
if(max==i+1){
count++;
}
}
return count;
}
边栏推荐
猜你喜欢
Win11勒索软件防护怎么打开?Win11安全中心勒索软件防护如何设置
开放麒麟 openKylin 版本规划敲定:10 月发布 0.9 版并开启公测,12 月发布 1.0 版

Interviewer: Tell me the difference between NIO and BIO
按键控制开关4017芯片数字电路
Is the code more messy?That's because you don't use Chain of Responsibility!

《社会企业开展应聘文职人员培训规范》团体标准在新华书店上架

七夕邂逅爱,那人一定在
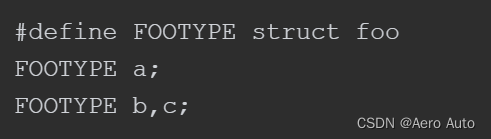
《C 陷阱与缺陷 》阅读概要
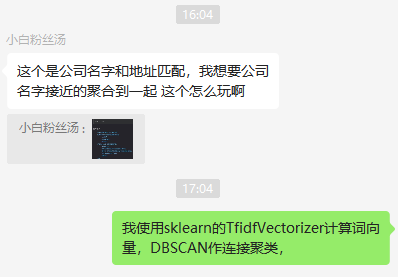
相似文本聚类与调参
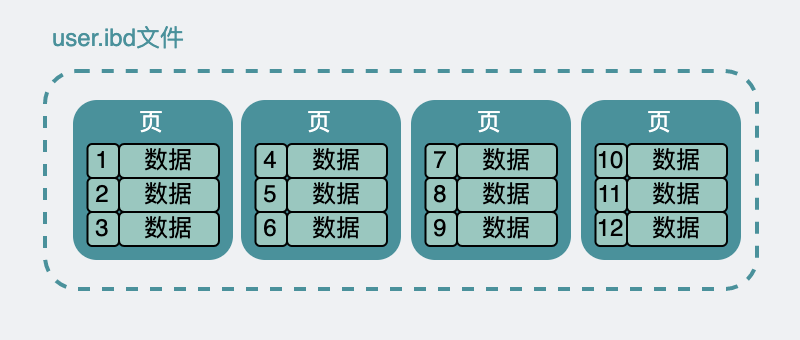
谁说 Mysql 单表最大 2000 W ?我硬要塞它 1 个亿
随机推荐
漏洞复现 - - - Alibaba Nacos权限认证绕过
This article sorts out the development of the main models of NLP
PAT甲级:1040 Longest Symmetric String
编程思想_编程有必要给孩子学吗?
LeetCode_299_猜数字游戏
php中的ceil和floo以及round函数「建议收藏」
让Web页面中的编辑器支持黏贴或直接拖拽来添加图片「建议收藏」
FreeConfig.h文件
国家安全机关对涉嫌危害国家安全犯罪嫌疑人杨智渊实施刑事拘传审查
VBS函数应用–getobject的使用获得Automation对象
错误 AttributeError type object 'Callable' has no attribute '_abc_registry' 解决方案
MySQL性能指标TPS\QPS\IOPS如何压测?
字符串类的设计与实现_C语言字符串编程题
17种正则表达式
手搓一个“七夕限定”,用3D Engine 5分钟实现烟花绽放效果
文字编码 - Markdown 简明教程
SLAM 05.视觉里程计-2-特征法
人像分割技术解析与应用
RT-Thread stm32 基础记录
【无标题】